1.60: Kinetic Energy Is Important in the Nanoscale World
- Page ID
- 156290
Most explanations of atomic and molecular phenomena found in textbooks are expressed in terms of potential-energy-only (PEO) models. Inclusion of kinetic energy in the analysis is generally considered to be unnecessary or irrelevant. This view is of questionable validity, and it is becoming increasing clear that ignoring kinetic energy at the nanoscopic level can lead to facile but incorrect explanations of atomic and molecular behavior. (1-4)
The idea that kinetic energy should not be ignored is not too surprising since quantum mechanical calculations involve minimization of the total energy, which includes both kinetic and potential energy contributions. In other words, kinetic energy plays an important role at the computational level, and therefore should not be excluded at the level of analysis and interpretation. For example, the fundamental questions regarding the stability of matter, the nature of the covalent bond, and the interaction of electromagnetic radiation with matter cannot be answered without a consideration of kinetic energy in the quantum mechanical context. (5)
The following simple variational calculation on a particle in a one-dimensional box with a linear internal potential clearly illustrates the importance of kinetic energy. For a particle of unit mass in a one-dimensional box of length one bohr (1ao =52.9 pm = 0.0529 nm) with internal potential energy V = 2x the Schrödinger equation in atomic units (h = 2\(\pi\)) is,
\[
\frac{-1}{2} \cdot \frac{\mathrm{d}^{2}}{\mathrm{d} \mathrm{x}^{2}} \Psi(\mathrm{x})+\mathrm{V}(\mathrm{x}) \cdot \Psi(\mathrm{x})=\mathrm{E} \cdot \Psi(\mathrm{x}) \quad \text { where } \quad \mathrm{V}(\mathrm{x}) :=2 \cdot \mathrm{x}
\nonumber \]
Three normalized trial wave functions are considered in this analysis, and are shown below both mathematically and graphically. The potential energy function is superimposed on the graphical representation of the trial wave functions.
\[
\Psi_{\mathrm{a}}(\mathrm{x}) :=\sqrt{2} \cdot \sin (\pi \cdot \mathrm{x}) \\ \Psi_{\mathrm{b}}(\mathrm{x}) :=\sqrt{105} \cdot \mathrm{x} \cdot(1-\mathrm{x})^{2} \\ \Psi_{\mathrm{c}}(\mathrm{x}) :=\sqrt{105} \cdot \mathrm{x}^{2} \cdot(1-\mathrm{x}) \\ \mathrm{x} :=0, 0.02 \ldots 1
\nonumber \]
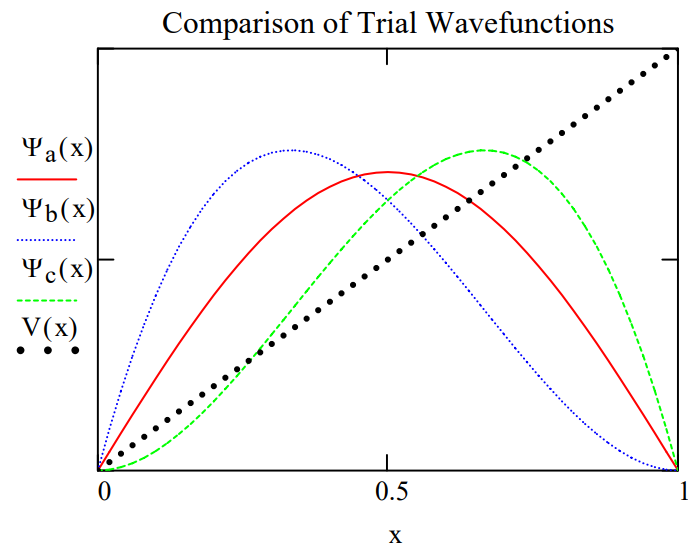
If asked to choose the best trial wave function by inspection, one would undoubtedly be inclined to select \(\Psi_{b}\) because it is skewed to the left side of the box where the potential energy is lowest. \(\Psi_{a}\) would be next best because it is symmetric, and \(\Psi_{c}\) would be last because it is skewed to the right side of the box where the potential energy is highest. However, the quantum mechanical calculations reveal that \(\Psi_{a}\) is the best trial function of the three because it gives the lowest total energy, the primary criterion of the variational principle.
For each trial wave function the expectation values for kinetic energy (T), potential energy (V), total energy (E = T + V), and position are calculated. Atomic units are used all calculations: 1Eh = 4.36 aJ and 1ao = 52.9 pm)
Calculations for trial wave function \(\Psi_{a}\)
| Kinetic energy: | \(\mathrm{T}_{\mathrm{a}} :=\int_{0}^{1} \Psi_{\mathrm{a}}(\mathrm{x}) \cdot-\frac{1}{2} \cdot \frac{\mathrm{d}^{2}}{\mathrm{d} \mathrm{x}^{2}} \Psi_{\mathrm{a}}(\mathrm{x}) \mathrm{d} \mathrm{x}\) | \(\mathrm{T}_{\mathrm{a}}=4.935\) |
| Potential energy: | \(\mathrm{V}_{\mathrm{a}} :=\int_{0}^{1} \Psi_{\mathrm{a}}(\mathrm{x}) \cdot 2 \cdot \mathrm{x} \cdot \Psi_{\mathrm{a}}(\mathrm{x}) \mathrm{d} \mathrm{x}\) | \(\mathrm{V}_{\mathrm{a}}=1.000\) |
| Total energy: | \(\mathrm{E}_{\mathrm{a}} :=\mathrm{T}_{\mathrm{a}}+\mathrm{V}_{\mathrm{a}}\) | \(\mathrm{E}_{\mathrm{a}}=5.935\) |
| Average position: | \(\mathrm{X}_{\mathrm{a}} :=\int_{0}^{1} \Psi_{\mathrm{a}}(\mathrm{x}) \cdot \mathrm{x} \cdot \Psi_{\mathrm{a}}(\mathrm{x}) \mathrm{d} \mathrm{x} \) | \(\mathrm{X}_{\mathrm{a}}=0.500\) |
Calculations for trial wave function \(\Psi_{b}\)
| Kinetic energy: | \(\mathrm{T}_{\mathrm{b}} :=\int_{0}^{1} \Psi_{\mathrm{b}}(\mathrm{x}) \cdot-\frac{1}{2} \cdot \frac{\mathrm{d}^{2}}{\mathrm{d} \mathrm{x}^{2}} \Psi_{\mathrm{b}}(\mathrm{x}) \mathrm{d} \mathrm{x}\) | \(\mathrm{T}_{\mathrm{b}}=7.000\) |
| Potential energy: | \(\mathrm{V}_{\mathrm{b}} :=\int_{0}^{1} \Psi_{\mathrm{b}}(\mathrm{x}) \cdot 2 \cdot \mathrm{x} \cdot \Psi_{\mathrm{b}}(\mathrm{x}) \mathrm{d} \mathrm{x}\) | \(\mathrm{V}_{\mathrm{b}}=0.750\) |
| Total energy: | \(\mathrm{E}_{\mathrm{b}} :=\mathrm{T}_{\mathrm{b}}+\mathrm{V}_{\mathrm{b}}\) | \(\mathrm{E}_{\mathrm{b}}=7.750\) |
| Average position: | \(\mathrm{X}_{\mathrm{b}} :=\int_{0}^{1} \Psi_{\mathrm{b}}(\mathrm{x}) \cdot \mathrm{x} \cdot \Psi_{\mathrm{b}}(\mathrm{x}) \mathrm{d} \mathrm{x} \) | \(\mathrm{X}_{\mathrm{b}}=0.375\) |
Calculations for trial wave function \(\Psi_{c}\)
| Kinetic energy: | \(\mathrm{T}_{\mathrm{c}} :=\int_{0}^{1} \Psi_{\mathrm{c}}(\mathrm{x}) \cdot-\frac{1}{2} \cdot \frac{\mathrm{d}^{2}}{\mathrm{d} \mathrm{x}^{2}} \Psi_{\mathrm{c}}(\mathrm{x}) \mathrm{d} \mathrm{x}\) | \(\mathrm{T}_{\mathrm{c}}=7.000\) |
| Potential energy: | \(\mathrm{V}_{\mathrm{c}} :=\int_{0}^{1} \Psi_{\mathrm{c}}(\mathrm{x}) \cdot 2 \cdot \mathrm{x} \cdot \Psi_{\mathrm{c}}(\mathrm{x}) \mathrm{d} \mathrm{x}\) | \(\mathrm{V}_{\mathrm{c}}=1.250\) |
| Total energy: | \(\mathrm{E}_{\mathrm{c}} :=\mathrm{T}_{\mathrm{c}}+\mathrm{V}_{\mathrm{c}}\) | \(\mathrm{E}_{\mathrm{c}}=8.250\) |
| Average position: | \(\mathrm{X}_{\mathrm{c}} :=\int_{0}^{1} \Psi_{\mathrm{c}}(\mathrm{x}) \cdot \mathrm{x} \cdot \Psi_{\mathrm{c}}(\mathrm{x}) \mathrm{d} \mathrm{x} \) | \(\mathrm{X}_{\mathrm{c}}=0.625\) |
These calculations are summarized in following table.
| Property\Wave function | Qa | Qb | Qc |
|---|---|---|---|
| Kinetic Energy/Eh | 4.935 | 7.000 | 7.000 |
| Potential Energy/Eh | 1.000 | 0.750 | 1.250 |
| Total Energy/Eh | 5.935 | 7.750 | 8.250 |
| Average Position/ao | 0.500 | 0.375 | 0.625 |
\(\Psi_{a}\) is a symmetric function which favors neither the low potential energy region nor the high potential energy region, but has the lowest total energy because it has a significantly lower kinetic energy than the other trial wave functions. The reason it has a lower kinetic energy is because it has a lower curvature than the other wave functions (curvature is the second derivative of the function). \(\Psi_{b}\) has a somewhat lower potential energy than \(\Psi_{a}\) because it favors the left side of the box, but consequentially a much higher kinetic energy because of its greater curvature. Total energy, as noted above, is what counts in a variational calculation. \(\Psi_{c}\) is the worst trial function because it has both high kinetic energy and high potential energy.
Of course, \(\Psi_{a}\) is not the best possible wave function for this problem; it is only the best of the three considered here. The best wave function can be found by a more elaborate variational calculation or by numerical integration of Schrödinger's equation. A Mathcad (6) program for numerical integration of Schrödinger's equation for a particle in a box with linear internal potential is given in the appendix.
This latter method yields a wave function with the following physical properties: = 4.942 Eh; = 0.983 Eh; = 5.925 Eh; = 0.491 ao. Note that this optimum wave function is skewed a little to the left of center, increasing kinetic energy slightly (+.007 Eh) and reducing potential energy slightly more (-.017 Eh), and overall yielding an energy reduction of -.01 Eh. The details of these calculations can be found in the appendix.
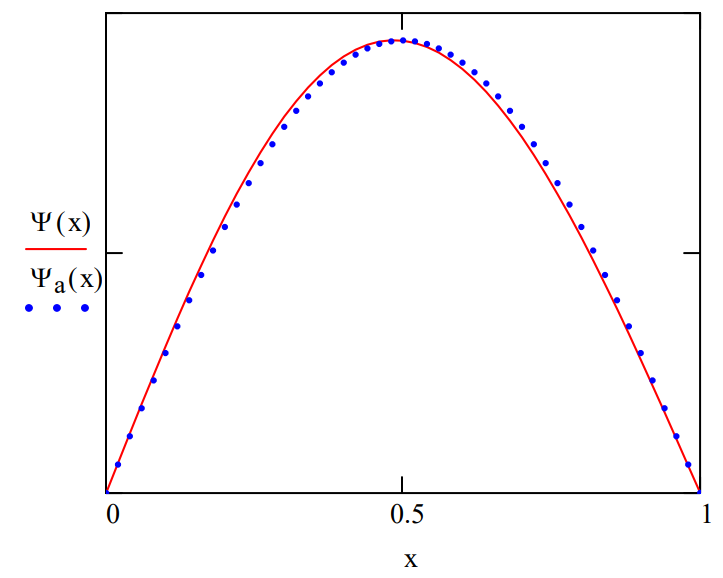
However, it is also important to note that \(\Psi_{a}\), the eigenfunction for the particle in a box problem [V(x)=0], is a very good trial wave function for this particular problem. It is in error by only 0.17% when compared with the more accurate, and essentially exact, numerical solution. \(\Psi_{a}\) is displayed along with the numerical wave function in the appendix to show how little it differs from the numerical solution.
Another point that should be noted is that \(\Psi_{b}\) does not become the preferred trial function until V(x) = 16.6x. In other words it requires a rather steeply rising internal potential energy to offset the kinetic energy advantage that \(\Psi_{a}\) has. The energy calculations for both wave functions are given below.
\[
\mathrm{V}_{\mathrm{a}} :=\int_{0}^{1} \Psi_{\mathrm{a}}(\mathrm{x}) \cdot 16.6 \cdot \mathrm{x} \cdot \Psi_{\mathrm{a}}(\mathrm{x}) \mathrm{d} \mathrm{x} \\ \mathrm{V}_{\mathrm{a}}=8.300 \qquad \mathrm{E}_{\mathrm{a}} :=\mathrm{T}_{\mathrm{a}}+\mathrm{V}_{\mathrm{a}} \qquad \mathrm{E}_{\mathrm{a}}=13.235
\nonumber \]
\[
\mathrm{V}_{\mathrm{b}} :=\int_{0}^{1} \Psi_{\mathrm{b}}(\mathrm{x}) \cdot 16.6 \cdot \mathrm{x} \cdot \Psi_{\mathrm{b}}(\mathrm{x}) \mathrm{d} \mathrm{x} \\ \mathrm{V}_{\mathrm{b}}=6.255 \qquad \mathrm{E}_{\mathrm{b}} :=\mathrm{T}_{\mathrm{b}}+\mathrm{V}_{\mathrm{b}} \qquad \mathrm{E}_{\mathrm{b}}=13.235
\nonumber \]
In conclusion, this simple example reveals that our intuition about the importance of potential energy in the analysis of physical phenomena at the nanoscale level should be tempered by a realization that the quantum mechanical nature of kinetic energy cannot be safely ignored.
Literature cited:
- Tokiwa, H.; Ichikawa, H. Int. J. Quantum Chem. 1994, 50, 109-112.
- Rioux, F.; DeKock, R. L. J. Chem. Educ. 1998, 75, 537-539.
- Weinhold, F. Nature 2001, 411, 539-541.
- Rioux, F. Chem. Educator 2003, 8, S1430-4171(03)01650-9; DOI 10.1333/s00897030650a..
- In the context of quantum mechanics, confinement energy is probably a better descriptor than kinetic energy, because the latter implies classical motion. According to quantum mechanical principles, confined particles, because of their wave-like charcter, are described by a weighted superposition of the allowed position eignestates. They are not executing a trajectory in the classical sense. In other words, they are not here and later there; they are here and there, simultaneously
- Mathcad 11 is a product of Mathsoft, Cambridge, MA 02142; www.mathsoft.com/.
Appendix
Numerical Solution for the Particle in a Slanted Box
Parameters:
\[
\mathrm{x}_{\max } :=1 \qquad \mathrm{m} :=1 \qquad \mathrm{V}_{0} :=2
\nonumber \]
Potential energy:
\[
\mathrm{V}(\mathrm{x}) :=\mathrm{V}_{0} \cdot \mathrm{x}
\nonumber \]
Solve Schrödinger's equation numerically:
Given
\[
\frac{-1}{2 \cdot \mathrm{m}} \cdot \frac{\mathrm{d}^{2}}{\mathrm{d} \mathrm{x}^{2}} \Psi(\mathrm{x})+\mathrm{V}(\mathrm{x}) \cdot \Psi(\mathrm{x})=\mathrm{E} \cdot \Psi(\mathrm{x}) \\ \Psi(0)=0 \qquad \Psi^{\prime}(0)=0.1 \\ \Psi :=\text { Odesolve }\left(\mathrm{x}, \mathrm{x}_{\mathrm{max}}\right)
\nonumber \]
Normalize wavefunction:
\[
\Psi(x) :=\frac{\Psi(x)}{\sqrt{\int_{0}^{x_{\max }} \Psi(x)^{2}} d x}
\nonumber \]
Enter energy guess: E = 5.925
Calculate most probable position:
\[
\mathrm{x} :=.5 \text { Given } \qquad \frac{\mathrm{d}}{\mathrm{dx}} \Psi(\mathrm{x})=0 \qquad \text { Find }(\mathrm{x})=0.485
\nonumber \]
Calculate average position:
\[
\mathrm{X}_{\mathrm{avg}} :=\int_{0}^{1} \Psi(\mathrm{x}) \cdot \mathrm{x} \cdot \Psi(\mathrm{x}) \mathrm{d} \mathrm{x} \qquad \mathrm{X}_{\mathrm{avg}}=0.491
\nonumber \]
Calculate potential and kinetic energy:
\[
\mathrm{V}_{\mathrm{avg}} :=\mathrm{V}_{0} \cdot \mathrm{X}_{\mathrm{avg}} \qquad \mathrm{V}_{\mathrm{avg}}=0.983
\nonumber \]
\[
\mathrm{T}_{\mathrm{avg}} :=\mathrm{E}-\mathrm{V}_{\mathrm{avg}} \qquad \mathrm{T}_{\mathrm{avg}}=4.942
\nonumber \]

