1.58: Quantized Gravitational States A Variational Approach
- Page ID
- 156287
Recently an international team of researchers at the Institute Laue-Langevin in Grenoble France published evidence for the quantized gravitational states of the neutron (1,2,3). The purpose of this paper is to analyze this phenomenon using the variational theorem.
Schrödinger’s equation for an object subject to a gravitational field near the surface of the earth is
\[
-\frac{h^{2}}{2 m} \frac{d^{2} \Psi(z)}{d z^{2}}+m g z \Psi(z)=E \Psi(z) \tag{1}
\nonumber \]
Equation (1) has an exact solution and the ground state energy for the neutron is given by
\[
E=2.3381\left(\frac{m g^{2} h^{2}}{2}\right)^{\frac{1}{3}}=2.254 \times 10^{-31} \mathrm{J} \tag{2}
\nonumber \]
where 2.3381 is the first root of the Airy function.
The performance of two trial wave functions for the “quantum bouncer” will be evaluated. The functions given in equations (3) and (4) were previously suggested for this purpose by J. L. Martin (4).
\[
\Psi(z)=2 \alpha^{\frac{3}{2}} z \exp (-\alpha z) \tag{3}
\nonumber \]
\[
\Phi(z)=\left(\frac{128 \beta^{3}}{\pi}\right)^{\frac{1}{4}} z \exp \left(-\beta z^{2}\right) \tag{4}
\nonumber \]
First Trial Wave Function
Evaluation of the variational integral for \(\Psi\)(z) yields
\[
\langle E\rangle=\int_{0}^{\infty} \Psi(z) \hat{H} \Psi(z) d z=\frac{h^{2} \alpha^{2}}{2 m}+\frac{3 m g}{2 \alpha} \tag{5}
\nonumber \]
Minimization of the energy provides the optimum value of \(\alpha\)
\[
\alpha=\left(\frac{3 m^{2} g}{2 h^{2}}\right)^{\frac{1}{3}} \tag{6}
\nonumber \]
and the ground-state energy.
\[
\langle E\rangle= 1.9656\left(m g^{2} h^{2}\right)^{\frac{1}{3}}=2.387 \times 10^{-31} \mathrm{J} \tag{7}
\nonumber \]
This result is in error by 6% indicating that \(\Psi\)(z) is a reasonable trial wave function for an object subjected to a confining gravitational interaction.
Second Trial Wave Function
It will be seen, however, that \(\Phi\)(z) is a much better trial wave function. Evaluation of the variational integral yields
\[
\langle E\rangle=\int_{0}^{\infty} \Phi(z) \hat{H} \Phi(z) d z=\frac{3 \hbar^{2} \beta}{2 m}+m g\left(\frac{2}{\pi \beta}\right)^{\frac{1}{2}} \tag{8}
\nonumber \]
Minimization of the energy provides the optimum value of \(\beta\)
\[
\beta=\left(\sqrt{\frac{2}{\pi}} \frac{m^{2} g}{3 h^{2}}\right)^{\frac{2}{3}} \tag{9}
\nonumber \]
and the ground-state energy.
\[
\langle E\rangle=\frac{3}{2}\left(\frac{6 m g^{2} h^{2}}{\pi}\right)^{\frac{1}{3}}=2.260 \times 10^{-31} \mathrm{J} \tag{10}
\nonumber \]
The error for this trial function is less 0.3%, so it is a very good approximation to the exact wave function.
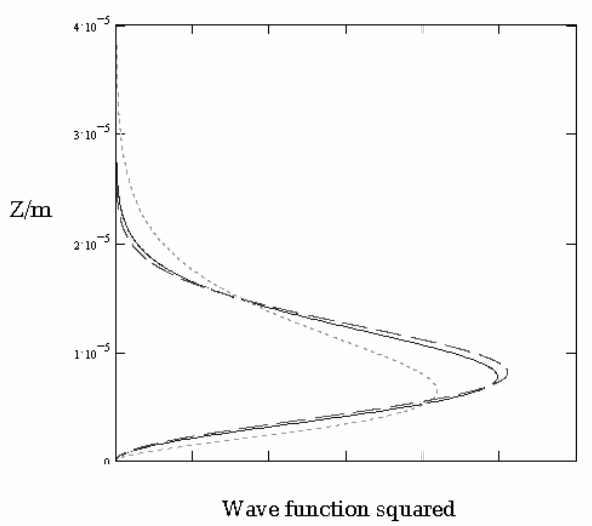
The trial wave functions are compared with the exact solution in Figure 1 (exact solution, solid blue; Ψ(z) green dots; \(\Phi\)(z) red dashes.
The Experiment
Thus far we have used the exact theoretical ground-state energy as a criterion to evaluate two trial wave functions. However, Nesvizhevsky and co-workers did not use energy or spectroscopy to gather evidence for the quantized gravitational states of the neutron.
This is impractical given how closely spaced the neutron gravitational states are. For example, the first excited state for the neutron is E2 = 3.941 x 10-31 J. Therefore, the energy difference between the ground state and first excited state is equivalent to a photon with a wavelength of 1.2 million meters. Clearly traditional spectroscopic methods cannot be used to establish the existence of quantized gravitational states for the neutron.
A schematic of the experiment Nesvizhevsky's team used to gather evidence for quantized neutron gravitational states is shown in Figure 2. The neutron is confined by the attractive gravitational field and the repulsive reflecting mirror surface. Ultra-cold neutrons (UCNs) with total velocities less than 8 m/s are "lobbed" into the apparatus. In the vertical direction the neutrons are subject to the gravitational interaction with the Earth, but there are no forces in the horizontal direction. The vertical and horizontal degrees of freedom are independent of one another in the design of this experiment, because care has been taken to eliminate vibrations, and extraneous electric and magnetic fields.

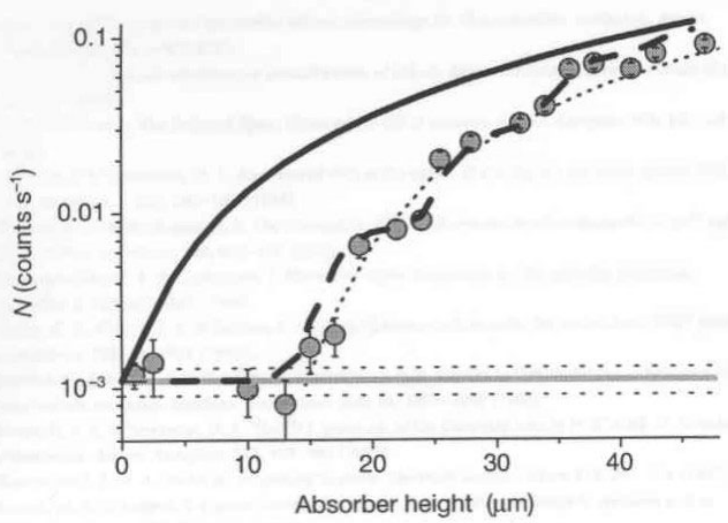
This apparatus records neutron throughput as a function of absorber height. The data collected are shown in Figure 3. The shaded circles are the actual data points. We will not be concerned with the solid, dashed, or dotted lines in the figure. The most important feature of the data for this analysis is the sharp increase in neutron throughput at about 20 \(\mu\)m.
Interpretation
The probability that a neutron will be found in the absorber, or the probability it will be absorbed is given by
\[
\int_{a_{z}}^{\infty}|\Phi(z)|^{2} d z \tag{11}
\nonumber \]
where az is the absorber height. Using the second trial wave function the probability is calculated for several absorber heights and displayed in the table below.
| Absorber height (\(\mu\)m) | Probability in Absorber |
|---|---|
| 10 | 0.388 |
| 15 | 0.078 |
| 20 | 0.007 |
| 25 | 3 x 10-4 |
It is clear from these calculations that the probability of finding the neutron in the absorber has declined significantly by 20 \(\mu\)m. This analysis, therefore, is consistent with the sharp increase in neutron throughput at this absorber height.
Literature cited:
- Nesvizhevsky, V.; et al. Quantum States of Neutrons in the Earth’s Gravitationsl Field. Nature 2002, 415, 297-299.
- Bowles, T. J. Quantum Effects of Gravity. Nature 2002, 415, 267-268.
- Rioux, F. Nature: Evidence for Quantized Gravitational States of the Neutron. J. Chem. Educ. 2002, 79, 1404-1406.
- Martin, J. L. Basic Quantum Mechanics; Clarendon Press, Oxford, 1981, p. 207.

