1.57: Evidence for Quantized Gravitational States of the Neutron

Last updated
Save as PDF

Page ID: 156286

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Particle confinement and the wave-like properties of matter lead, according to quantum mechanical principles, to self-interference which is the origin of energy quantization. The particle-in-a-box problem is used in introductory quantum mechanics courses to illustrate this fundamental quantum effect.

Terrestrial objects are confined by the Earth's gravitational field, but the quantum effects of gravity are not observed in the macro-world because the gravitational interaction is weak. Thus, the gravitational energy levels are very closely spaced and for all practical purposes form a continuum.

In spite of the lack of evidence for quantized gravitational energy levels, the "quantum bouncer" has been a favorite example in the repertoire of solvable one-dimensional problems for those who teach quantum chemistry and quantum physics. Schrödinger's equation for the quantum bouncer near the surface of the Earth is,

\[
-\frac{\hbar^{2}}{2 m} \frac{d^{2} \Psi(z)}{d z^{2}}+m g z \Psi(z)=E \Psi(z)
\nonumber \]

where the particle is confined by the impenetrable potential barrier of the Earth's surface (V = �) and the attractive gravitational interaction (V = mgz for z > 0).

The energy eigenvalues for the quantum bouncer are (1,2,3),

\[
E_{i}=\left(\frac{\hbar^{2} g^{2} m}{2}\right)^{\frac{1}{3}} a_{i}
\nonumber \]

where a_i are the roots of the Airy function. The first five roots are 2.33810, 4.08794, 5.52055, 6.78670, and 7.94413.

The associated eigenfunctions are,

\[
\Psi_{i}(z)=N_{i} A i\left[\left(\frac{2 m^{2} g}{\hbar^{2}}\right)^{1 / 3} z-a_{i}\right]
\nonumber \]

where

\[
N_{i}=\left(\int_{0}^{\infty} \Psi_{i}(z)^{2} d z\right)^{-1 / 2}
\nonumber \]

Because there is no analytical expression for the eigenfunctions each one must be normalized using a numeric algorithm.

Very recently an international team at the Institute Laue-Langevin in Grenoble France lead by V. Nesvizhevsky (4) published evidence for the quantized gravitational states of the neutron. To read a short summary of this experiment in Nature Magazine by Thomas Bowles (5) click here. Another summary has just been published in Physics Today. (6)

To appreciate the significance of this accomplishment we calculate the neutron's ground state energy and wave function in the Earth's gravitational field using the equations above. The mass of the neutron is 1.675x10^-27 kg which yields a ground-state energy of E₁ = 2.254x10^-31 J. This corresponds to a classical vertical velocity of 1.6 cm/s. Thus gravitational confinement requires a source of ultra-cold neutrons (UCNs).

Furthermore, the energy of the first excited state is 3.941x10^-31 J, so the energy difference between the ground state and the first excited state is equivalent to photon with a wavelength of 1.2x10⁶ m. Clearly traditional spectroscopic methods cannot be used to establish the existence of quantized gravitational states for the neutron.

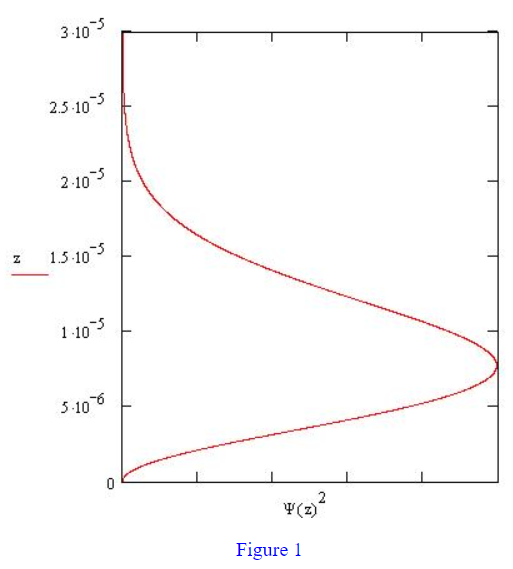
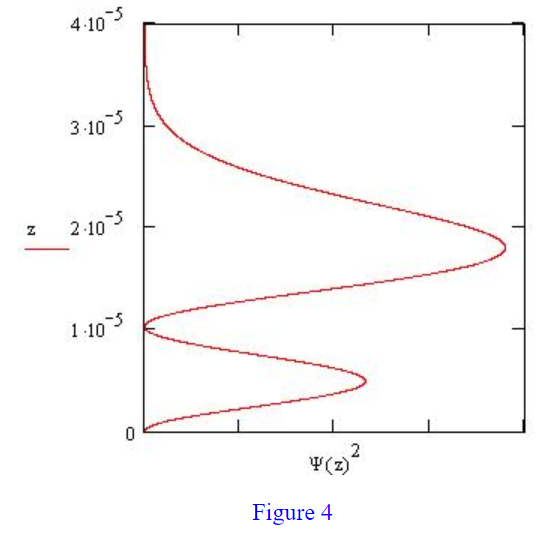
The probability distributions, \(\Psi\)(z)², for the ground and first excited states are shown in Figures 1 and 4. They hold the key to the experimental design that Nesvizhevsky's and his group used to establish that the neutron's gravitational states are quantized. To down-load a Mathcad file that will generate the neutron eigenstates numerically click here.

Figure 2. The neutron is confined by the attractive gravitational field and the repulsive reflecting mirror surface. Ultra-cold neutrons (UCNs) with total velocities less than 8 m/s are "lobbed" into the apparatus. In the vertical direction the neutrons are subject to the gravitational interaction with the Earth, but there are no forces in the horizontal direction. The vertical and horizontal degrees of freedom are independent of one another in the design of this experiment, because care has been taken to eliminate vibrations, and extraneous electric and magnetic fields.

Figure 2 [Reprinted by permission from Nature (Volume **415** page 267) copyright 2002 Macmillan Publishers Ltd.]

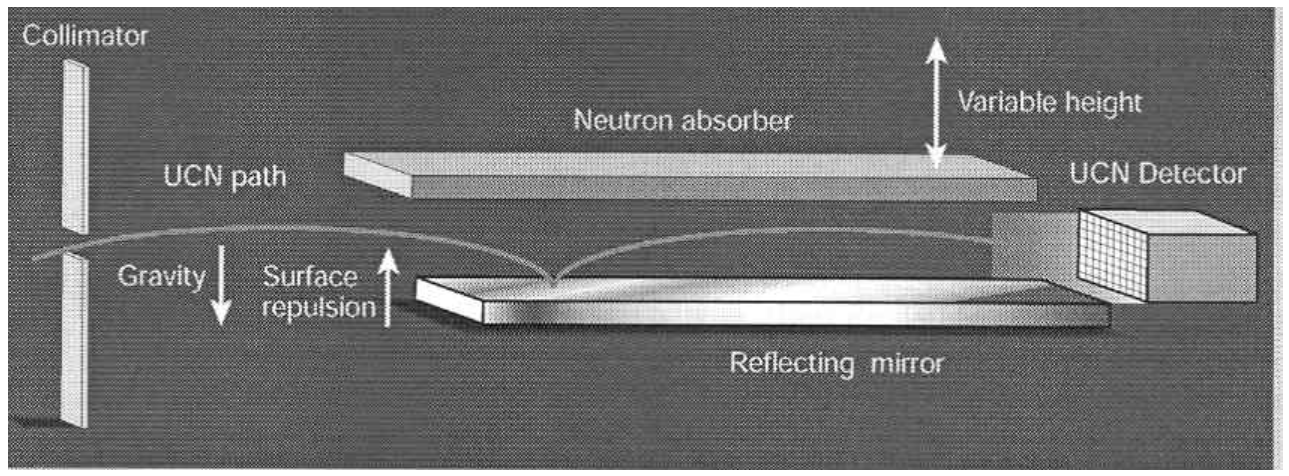
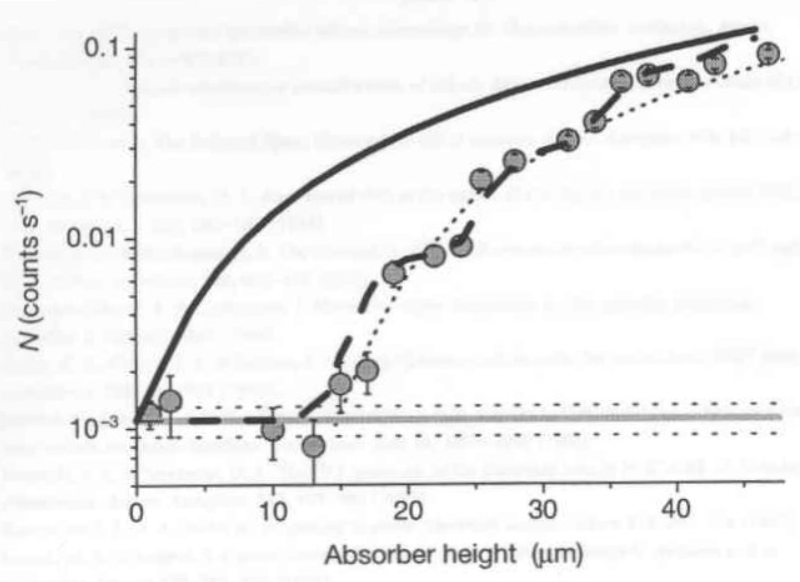
The apparatus shown in Figure 2 records neutron throughput as a function of absorber height. The data collected are shown in Figure 3. The shaded circles are the actual data points. We will not be concerned with the solid, dashed, or dotted lines in the figure. The most important feature of the data for this analysis is the sharp increase in neutron throughput at about 20 \(\mu\)m.

Figure 3 [Reprinted by permission from Nature (Volume **415** page 299) copyright 2002 Macmillan Publishers Ltd.]

The argument will be made that the neutron wave function shown in Figure 1 is consistent with the data presented in Figure 3. To demonstrate this we calculate the probability that the ground-state neutron will be found in the absorber for a variety of absorber heights. This requires numerical evaluation of

\[
\int_{a_{z}}^{\infty} \Psi_{1}(z)^{2} d z
\nonumber \]

where a_z is the absorber height. These calculations are presented in the table given below.

Absorber height/mm	Probability in Absorber
10	0.380
15	0.089
20	0.012
25	0.001

It is clear from these calculations and Figure 1 that the probability of finding the neutron in the absorber falls off sharply at about 20 \(\mu\)m. This analysis, therefore, is consistent with the sharp increase in neutron throughput at this absorber height.

Many neutron gravitational states besides the ground state are occupied and it is therefore necessary to explore the experimental implications of this fact. The first excited state is, as mentioned previously, shown in Figure 4. This wave function extends further in the z-direction than the ground state function, going to zero around 35 \(\mu\)m. The experimental significance of this is that the neutron throughput should show another abrupt increase in the neighborhood of 30 \(\mu\)m, an absorber height for which, the first excited state neutrons have a low probability of being absorbed. This phenomena should be repeated for all other occupied excited states as the absorber reaches the spatial extent of each excited state wave function.

With regard to this expected effect Bowles has commented (5)

The data show some hint of stepped increases at the values corresponding to higher energy states, consistent with the existence of these states, but they are not yet conclusive. Nonetheless, the evidence for the existence of the first energy state is convincing and confirms that a quantum effect occurs in the gravitational trap. The difficulty of this measurement should not be underestimated. The researchers are measuring a quantum effect caused by gravity that requires a resolution of 10^-15 eV. Interactions of the neutrons with other fields would normally obscure such a tiny effect, but the neutron's lack of electric charge and the low kinetic energy of the UCNs make such observations possible.

In summary, thanks to Nesvizhevsky and his team, we now have some direct evidence for quantized gravitational states. The "quantum bouncer", previously a purely academic exercise, can now be applied to a real-life example.

Literature cited:

P. W. Langhoff, "Schrödinger particle in a gravitational well," Am. J. Phys. 39, 954-957 (1971).
R. L. Gibbs, "The quantum bouncer," Am. J. Phys. 43, 25-28 (1975).
J. Gea-Banacloche, "A quantum bouncing ball," Am. J. Phys. 67, 776-782 (1999).
V. Nesvizhevsky, et al., "Quantum states of neutrons in the Earth's gravitational field," Nature 415 297-299 (2002).
T. J. Bowles, "Quantum effects of gravity," Nature 415 267-268 (2002).
B. Schwartzchild, "Ultracold Neutrons Exhibit Quantu States in the Earth's Gravitational Field," Physics Today 55 (3) 20-23 (2002).