1.55: Using a Mach-Zehnder Interferometer to Illustrate Feynman's Sum Over Histories Approach to Quantum Mechanics
- Page ID
- 155911
Thirty-one years ago Dick Feynman told me about his 'sum over histories' version of quantum mechanics. "The electron does anything it likes," he said. "It just goes in any direction, at any speed, forward and backward in time, however it likes, and then you add up the amplitudes and it gives you the wave function." I said to him "You're crazy." But he isn't. Freeman Dyson, 1980.
In Volume 3 of the celebrated Feynman Lectures on Physics, Feynman uses the double-slit experiment as the paradigm for his 'sum over histories' approach to quantum mechanics. He said that any question in quantum mechanics could be answered by responding, "You remember the experiment with the two holes? It's the same thing." And, of course, he's right.
A 'sum over histories' is a superposition of probability amplitudes for the possible experimental outcomes which in quantum mechanics carry phase and therefore interfer constructively and destructively with one another. The square of the magnitude of the superposition of histories yields the probabilities that the various experimental possibilities will be observed.
Obviously it takes a minum of two 'histories' to demonstrate the interference inherent in the quantum mechanical superposition. And, that's why Feynman chose the double-slit experiment as the paradigm for quantum mechanical behavior. The two slits provide two paths, or 'histories' to any destination on the detection screen. In this tutorial a close cousin of the double-slit experiment, single particle interference in a Mach-Zehnder interferometer, will be used to illustrate Feynman's 'sum over histories' approach to quantum mechanics.
A Beam Splitter Creates a Quantum Mechanical Superposition
Single photons emitted by a source (S) illuminate a 50-50 beam splitter (BS). Mirrors (M) direct the photons to detectors D1 and D2. The probability amplitudes for transmission and reflection are given below. By convention a 90 degree phase shift (i) is assigned to reflection.
Probability amplitude for photon transmission at a 50-50 beam splitter:
\[
\langle T | S\rangle=\frac{1}{\sqrt{2}}
\nonumber \]
Probability amplitude for photon reflection at a 50-50 beam splitter:
\[
\langle R | S\rangle=\frac{i}{\sqrt{2}}
\nonumber \]
After the beam splitter the photon is in a superposition state of being transmitted and reflected.
\[
|S\rangle \rightarrow \frac{1}{\sqrt{2}}[|T\rangle+ i|R\rangle]
\nonumber \]
As shown in the diagram below, mirrors reflect the transmitted photon path to D2 and the reflected path to D1. The source photon is expressed in the basis of the detectors as follows.
\[
|S\rangle \rightarrow \frac{1}{\sqrt{2}}[|T\rangle+ i|R\rangle] \xrightarrow[R \rightarrow D_{1}]{T \rightarrow D_{z}} \rightarrow \frac{1}{\sqrt{2}}\left[\left|D_{2}\right\rangle+ i\left|D_{1}\right\rangle\right]
\nonumber \]
The square of the magnitude of the coefficients of D1 and D2 give the probabilities that the photon will be detected at D1 or D2. Each detector registers photons 50% of the time. In other words, in the quantum view the superposition collapses randomly to one of the two possible measurement outcomes it represents.
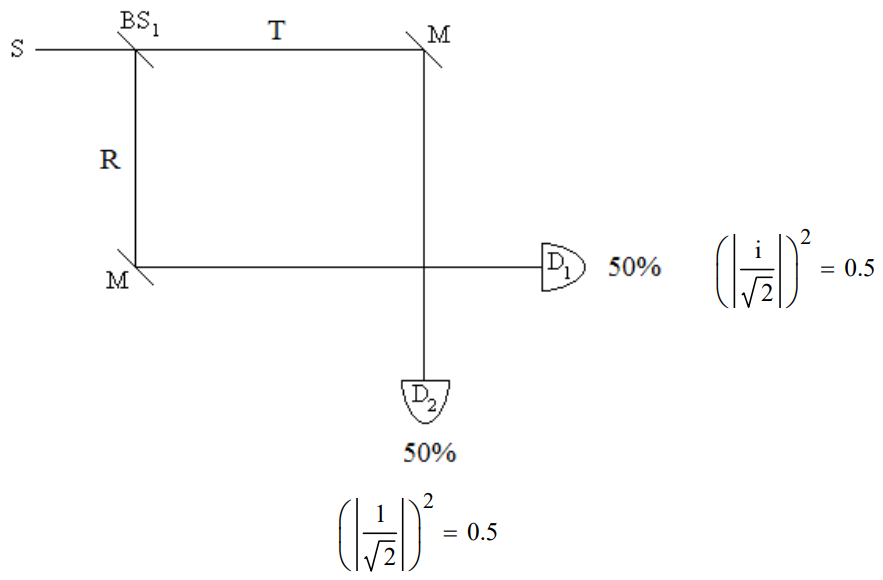
The classical view that detection at D1 means the photon was reflected at BS1 and that detection at D2 means it was transmitted at BS1 is not tenable as will be shown using a Mach-Zehnder interferometer which has a second beam splitter at the path intersection before the detectors.
A Second Beam Splitter Provides Two Paths to Each Detector
If a second beam splitter is inserted before the detectors the photons always arrive at D1. In the first experiment there was only one path to each detector. The construction of a Mach-Zehnder interferometer by the insertion of a second beam splitter creates a second path to each detector and the opportunity for constructive and destructive interference on the paths to the detectors.

Given the superposition state after BS1, the probability amplitudes after BS2 interfere constructively at D1 and destructively at D2.
\[\begin{matrix} \text{After}\;BS_{1} & \; & \text{After}\;BS_{2} & \; & \text{Final State} \\ \; & \; & |T\rangle \rightarrow \frac{1}{\sqrt{2}}\left[i\left|D_{1}\right\rangle+\left|D_{2}\right\rangle\right] & \; & \; \\ |S\rangle \rightarrow \frac{1}{\sqrt{2}}[|T\rangle+ i|R\rangle] & \rightarrow & + & \rightarrow & i\left|D_{1}\right\rangle \\ \; & \; & i|R\rangle \rightarrow \frac{i}{\sqrt{2}}\left[\left|D_{1}\right\rangle+ i\left|D_{2}\right\rangle\right] & \; & \; \end{matrix} \nonumber \]
Adopting the classical view that the photon is either transmitted or reflected at BS1 does not produce this result. If the photon was transmitted at BS1 it would have equal probability of arriving at either detector after BS2. If the photon was reflected at BS1 it would also have equal probability of arriving at either detector after BS2. The predicted experimental results would be the same as those of the single beam splitter experiment. In summary, the quantum view that the photon is in a superposition of being transmitted and reflected after BS1 is consistent with both experimental results described above; the classical view that it is either transmitted or reflected is not.
Some disagree with this analysis saying the two experiments demonstrate the dual, complementary, behavior of photons. In the first experiment particle-like behavior is observed because both detectors register photons indicating the individual photons took one path or the other. The second experiment reveals wave-like behavior because interference occurs - only D1 registers photons. According to this view the experimental design determines whether wave or particle behavior will occur and somehow the photon is aware of how it should behave. Suppose in the second experiment that immediately after the photon has interacted with BS1, BS2 is removed. Does what happens at the detectors require the phenomenon of retrocausality or delayed choice? Only if you reason classically about quantum experiments.
We always measure particles (detectors click, photographic film is darkened, etc.) but we interpret what happened or predict what will happen by assuming wavelike behavior, in this case the superposition created by the initial beam splitter that delocalizes the position of the photon. Quantum particles (quons) exhibit both wave and particle properties in every experiment. To paraphrase Nick Herbert (Quantum Reality), particles are always detected, but the experimental results observed are the result of wavelike behavior. Richard Feynman put it this way (The Character of Physical Law), "I will summarize, then, by saying that electrons arrive in lumps, like particles, but the probability of arrival of these lumps is determined as the intensity of waves would be. It is in this sense that the electron behaves sometimes like a particle and sometimes like a wave. It behaves in two different ways at the same time (in the same experiment)." Bragg said, "Everything in the future is a wave, everything in the past is a particle."
In 1951 in his treatise Quantum Theory, David Bohm described wave-particle duality as follows: "One of the most characteristic features of the quantum theory is the wave-particle duality, i.e. the ability of matter or light quanta to demonstrate the wave-like property of interference, and yet to appear subsequently in the form of localizable particles, even after such interference has taken place." In other words, to explain interference phenomena wave properties must be assigned to matter and light quanta prior to detection as particles.
Matrix Mechanics Approach
As a companion analysis, the matrix mechanics approach to single-photon interference in a Mach-Zehnder interferometer is outlined next.
State Vectors
Photon moving horizontally:
\[\mathrm{x} :=\left(\begin{array}{l}{1} \\ {0}\end{array}\right) \nonumber \]
Photon moving vertically:
\[\mathrm{y} :=\left(\begin{array}{l}{0} \\ {1}\end{array}\right) \nonumber \]
Operators
Operator representing a beam splitter:
\[
\mathrm{BS} :=\frac{1}{\sqrt{2}} \cdot\left(\begin{array}{cc}{1} & {\mathrm{i}} \\ {\mathrm{i}} & {1}\end{array}\right)
\nonumber \]
Operator representing a mirror:
\[
\mathrm{M} :=\left(\begin{array}{ll}{0} & {1} \\ {1} & {0}\end{array}\right)
\nonumber \]
Single beam splitter example:
Reading from right to left.
The probability that a photon leaving the source moving in the (horizontal) x-direction, encountering a beam splitter and a mirror will be detected at D1.
\[
\left(|\mathrm{x}^{\mathrm{T}} \cdot \mathrm{M} \cdot \mathrm{BS} \cdot \mathrm{x}|\right)^{2}=0.5
\nonumber \]
The probability that a photon leaving the source moving in the (horizontal) x-direction, encountering a beam splitter and a mirror will be detected at D2.
\[
\left(|\mathrm{y}^{\mathrm{T}} \cdot \mathrm{M} \cdot \mathrm{BS} \cdot \mathrm{x}|\right)^{2}=0.5
\nonumber \]
Two beam splitter example (MZI):
The probability that a photon leaving the source moving in the (horizontal) x-direction, encountering a beam splitter, a mirror and another beam splitter will be detected at D1.
\[
\left(|\mathrm{x}^{\mathrm{T}} \cdot \mathrm{BS} \cdot \mathrm{M} \cdot \mathrm{BS} \cdot \mathrm{x}|\right)^{2}=1
\nonumber \]
The probability that a photon leaving the source moving in the (horizontal) x-direction, encountering a beam splitter, a mirror and another beam splitter will be detected at D2.
\[
\left(|\mathrm{y}^{\mathrm{T}} \cdot \mathrm{BS} \cdot \mathrm{M} \cdot \mathrm{BS} \cdot \mathrm{x}|\right)^{2}=0
\nonumber \]

