1.54: An Analysis of Three-Slit Interference

Quantum mechanics teaches that if there is more than one path to a particular destination interference effects are likely. Using Feynmanʹs ʹsum over historiesʹ approach to quantum mechanics the probability of arrival at a location is the square of the magnitude of the sum of the probability amplitudes for each path to that location. For example, in the triple‐slit diffraction experiment the probability of a photon leaving a source and arriving at x on the detection screen shows three‐path interference.

\[P_{123}=|\langle x \mid 1\rangle\langle 1 \mid S\rangle+\langle x \mid 2\rangle\langle 2 \mid S\rangle+\langle x \mid 3\rangle\langle 3 \mid S\rangle|^{2} \label{1} \]

However, Sinha et al. [Science 329, 418 (2010)] argue that true interference only occurs between pairs of paths. In this case between paths 1 & 2, 1 & 3, and 2 & 3. Sinhaʹs interpretation of triple‐slit diffraction leads to an expression that is complex when compared to the lean equation above.

\[P_{123}=|\langle x \mid 1\rangle\langle 1 \mid S\rangle+\langle x \mid 2\rangle\langle 2 \mid S\rangle|^{2}+|\langle x \mid 1\rangle\langle 1 \mid S\rangle+\langle x \mid 3\rangle\langle 3 \mid S\rangle|^{2}+|\langle x \mid 2\rangle\langle 2 \mid S\rangle+\langle x \mid 3\rangle\langle 3 \mid S\rangle|^{2} -|\langle x \mid 1\rangle\langle 1 \mid S\rangle|^{2}-|\langle x \mid 2\rangle\langle 2 \mid S\rangle|^{2}-|\langle x \mid 3\rangle\langle 3 \mid S\rangle|^{2}\label{2} \]

It will now be shown that the two expressions, as they must, lead to the same calculated diffraction pattern. My question is whether there is any real physical significance to Sinhaʹs reinterpretation of multi‐path interference in terms of two‐path interference effects.

We begin with the traditional approach of writing the photon wave function as a superposition of being at all three slits and then Fourier transforming it into momentum space to give the diffraction pattern.

number of slit: \(\mathrm{n}:=3\)

Slit position: \(\mathrm{j}:=1 . . \mathrm{n} \quad \mathrm{x}_{\mathrm{j}}:=\mathrm{j}\)

Slit width: \(\delta:=.2\)

Calculate diffraction pattern: \(\left.\Psi(\mathrm{p}):=\left(\mid \sum_{j=1}^{\mathrm{n}} \int_{\mathrm{x}_{\mathrm{j}}-\frac{\delta}{2}}^{x_{\mathrm{j}}+\frac{\delta}{2}} \frac{1}{\sqrt{2 \cdot \pi}} \cdot \exp (-\mathrm{i} \cdot \mathrm{p} \cdot \mathrm{x}) \cdot \frac{1}{\sqrt{\delta}} \mathrm{d} \mathrm{x}\right]\right)^{2}\)

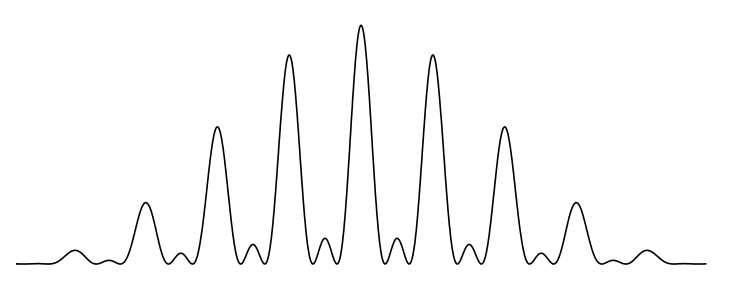
Next, following Sinha, the diffraction pattern is recalculated using equation (\ref{2}). This equation is a generalization of the double‐slit probability expression as shown in the Appendix.

\[P_{123}=P_{1}+P_{2}+P_{3}+I_{12}+I_{13}+I_{23}=P_{12}+P_{13}+P_{23}-P_{1}-P_{2}-P_{3} \nonumber \]

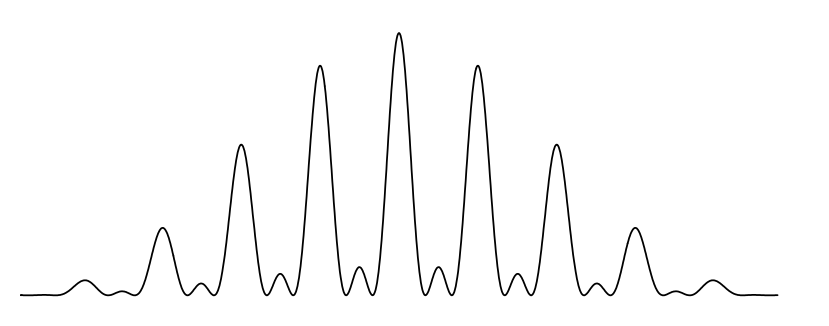
Franson [Science 329, 396 (2010)] summarized this view as follows: "Quantum interference between many different pathways is simply the sum of the effects from all pairs of pathways." If that is so why is it necessary to subtract the single‐slit diffraction patterns?

\(P_{1 \text { slit }}(p):=\left(\left\lfloor\int_{-\frac{\delta}{2}}^{\frac{\delta}{2}} \frac{1}{\sqrt{2 \cdot \pi}} \cdot \exp (-i \cdot p \cdot x) \cdot \frac{1}{\sqrt{\delta}} d x\right]\right)^{2}\)

\[\begin{align*} \Psi(\mathrm{p}) &=\left( \left| \int_{1-\frac{\delta}{2}}^{1+\frac{\delta}{2}} \frac{1}{\sqrt{2 \cdot \pi}} \cdot \exp (-\mathrm{i} \cdot \mathrm{p} \cdot \mathrm{x}) \cdot \frac{1}{\sqrt{\delta}} \mathrm{d} \mathrm{x}+\int_{2-\frac{\delta}{2}}^{2+\frac{\delta}{2}} \frac{1}{\sqrt{2 \cdot \pi}} \cdot \exp (-\mathrm{i} \cdot \mathrm{p} \cdot \mathrm{x}) \cdot \frac{1}{\sqrt{\delta}} \mathrm{dx}\right | \right)^{2} \\[4pt] &+ \left( \left| \int_{1-\frac{\delta}{2}}^{1+\frac{\delta}{2}} \frac{1}{\sqrt{2 \cdot \pi}} \cdot \exp (-\mathrm{i} \cdot \mathrm{p} \cdot \mathrm{x}) \cdot \frac{1}{\sqrt{\delta}} \mathrm{d} \mathrm{x}+\int_{3-\frac{\delta}{2}}^{3+\frac{\delta}{2}} \frac{1}{\sqrt{2 \cdot \pi}} \cdot \exp (-\mathrm{i} \cdot \mathrm{p} \cdot \mathrm{x}) \cdot \frac{1}{\sqrt{\delta}} \mathrm{d} \mathrm{x}\right | \right)^{2}\\[4pt] &+ \left( \left| \int_{2-\frac{\delta}{2}}^{2+\frac{\delta}{2}} \frac{1}{\sqrt{2 \cdot \pi}} \cdot \exp (-\mathrm{i} \cdot \mathrm{p} \cdot \mathrm{x}) \cdot \frac{1}{\sqrt{\delta}} \mathrm{d} \mathrm{x}+\int_{3-\frac{\delta}{2}}^{3+\frac{\delta}{2}} \frac{1}{\sqrt{2 \cdot \pi}} \cdot \exp (-\mathrm{i} \cdot \mathrm{p} \cdot \mathrm{x}) \cdot \frac{1}{\sqrt{\delta}} \mathrm{d} \mathrm{x}\right | \right)^{2} \\[4pt] &+-3 \left( \left | \int_{-\frac{\delta}{2}}^{\frac{\delta}{2}} \frac{1}{\sqrt{2 \cdot \pi}} \cdot \exp (-\mathrm{i} \cdot \mathrm{p} \cdot \mathrm{x}) \cdot \frac{1}{\sqrt{\delta}} \mathrm{dx}\right|\right)^{2} \end{align*} \]

A 1980 reminiscence by Freeman Dyson is relevant to my critque.

Thirty‐one years ago Dick Feynman told me about his ʹsum over historiesʹ version of quantum mechanics. "The electron does anything it likes," he said. "It just goes in any direction, at any speed, forward and backward in time, however it likes, and then you add up the amplitudes and it gives you the wave function." I said to him "Youʹre crazy." But he isnʹt.

It is obvious from Feynmanʹs description of his ʹsum over historiesʹ approach to quantum interference that it puts no restriction on the number of interfering probability amplitudes.

The conceptual and mathematical clarity of Equation (\ref{1}) is lost in the transition to Equation (\ref{2}), which consists of three two‐path interferences and three single‐slit diffraction terms. Consequently Equation (\ref{2}) does not actually show that the triple‐slit experiment involves only the interference of pairs of paths.

Appendix

The probability expression for an event involving two equivalent paths is

\[P_{i j}=\left|\Psi_{i}+\Psi_{j}\right|^{2}=\left|\Psi_{i}\right|^{2}+\left|\Psi_{j}\right|^{2}+\Psi_{i}^{*} \Psi_{j}+\Psi_{j}^{*} \Psi_{i}=P_{i}+P_{j}+I_{i j} \nonumber \]

where \(I_{ij}\) is the interference term and Pi is defined as the probability when only the \(i_{th}\) path is open. It is my opinion that this latter designation is not strictly valid. However, accepting it for the time being leads to the following definition for two‐path interference.

\[I_{i j}=P_{i j}-P_{i}-P_{j} \nonumber \]

Therefore, the probability for an event involving three equivalent paths to a destination using only two‐path interference is,

\[P_{123}=P_{1}+P_{2}+P_{3}+I_{12}+I_{13}+I_{23}=P_{12}+P_{13}+P_{23}-P_{1}-P_{2}-P_{3} \nonumber \]