1.107: The Bloch Sphere
- Page ID
- 160265
The eigenfunctions of the Pauli spin matrices.
\[ \begin{matrix} \sigma_z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} & \sigma_x = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} & \sigma_y = \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix} \end{matrix} \nonumber \]
are presented mathematically and shown on the Bloch sphere below. The Xu state is highlighted.
\[ \begin{matrix} Z_u = \begin{pmatrix} 1 \\ 0 \end{pmatrix} & Z_d = \begin{pmatrix} 0 \\ 1 \end{pmatrix} & X_u = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ 1 \end{pmatrix} & X_d = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ -1 \end{pmatrix} & Y-u = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ i \end{pmatrix} & Y_d = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ -i \end{pmatrix} \end{matrix} \nonumber \]
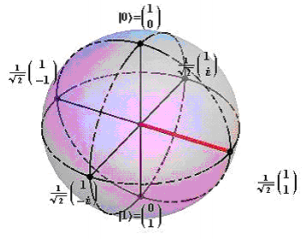
This figure was taken from demonstrations.wolfram.com/QubitsOnThePoincareBlochSphere/ a contribution by Rudolf Muradian. The Bloch sphere is prepared in Cartesian coordinates using Mathcad graphics.
\[ \begin{matrix} \text{numpts} = 100 & i = 0 .. \text{numpts} & j = 0 .. \text{numpts} & \theta_i = \frac{ \pi i}{ \text{numpts}} & \phi_j = \frac{2 \pi j}{ \text{numpts}} \end{matrix} \nonumber \]
\[ \begin{matrix} X_{i,~j} = \sin \left( \theta_i \right) \cos \left( \phi_j \right) & Y_{i,~j} = \sin \left( \theta_i \right) \sin \left( \phi_j \right) & Z_{i,~j} = \cos \left( \theta_i \right) \end{matrix} \nonumber \]
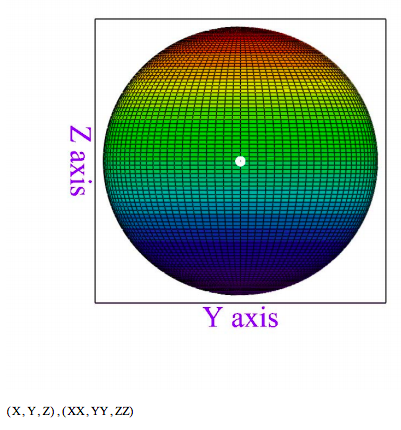
Next, the coordinates of a quantum qubit are calculated and displayed on the Bloch sphere as a white dot. As the polar and azmuthal angles are changed, you will need to rotate the figure to see where the white dot is on the surface of the Bloch sphere.
\[ \begin{matrix} \theta 1 = \frac{ \pi}{2} & \phi 1 = 0 & \Psi ( \theta 1,~ \phi 1 ) = \cos \left( \frac{ \theta 1}{2} \right) \begin{pmatrix} 1 \\ 0 \end{pmatrix} + \text{exp} ( i \phi 1) \sin \left( \frac{ \theta 1}{2} \right) \begin{pmatrix} 0 \\ 1 \end{pmatrix} & \Psi ( \theta 1,~ \phi 1) = \begin{pmatrix} 0.707 \\ 0.707 \end{pmatrix} \end{matrix} \nonumber \]
\[ \begin{matrix} XX_{i,~j} = \sin ( \theta 1) \cos ( \phi 1) & YY_{i,~j} = \sin ( \theta 1) \sin ( \phi 1) & ZZ_{i,~j} = \cos ( \theta 1) \end{matrix} \nonumber \]