1.2: Atomic and Molecular Stability
- Page ID
- 133065
Klaus Ruedenberg once wrote that there are no ground states in classical mechanics. In other words, quantum principles are required to understand the stability of atoms and molecules, and the nature of the chemical bond. Quantum mechanics is not mathematically more difficult than classical physics, the real challenge it offers is of a conceptual nature. That’s because it says that understanding the stability of matter requires that it possess both particle and wave properties. The conceptual challenge is that particle and wave are contradictory concepts.
Wave-Particle Duality for Matter and Light
A wave is spatially delocalized
A particle is spatially localized
•
These incompatible concepts are united by the deBroglie wave equation with the wave property (wavelength) on the left and the particle property (momentum) on the right in a reciprocal relationship mediated by the ubiquitous Planck’s constant.
\[\lambda = \frac{h}{m \nu} \nonumber \]
Investing matter with wave behavior subjects it to interference effects and leads immediately to a redefinition of kinetic energy. In quantum mechanics the concept kinetic energy should be replaced with confinement energy, because the former implies classical motion. According to quantum mechanical principles a confined particle, a quon, because of its wave-like character is described by a wave function which is a weighted superposition of all possible positions. Quons do not execute trajectories in the classical sense. They are not here and later there; they are here and there simultaneously. As Werner Heisenberg said, “There is no space-time inside the atom.” In other words there is also no space-time for confined quons.
“A quon is any entity (electron, proton, neutron, atom, molecule, C60 etc.), no matter how immense, that exhibits both wave and particle aspects in the peculiar quantum manner.” Nick Herbert, Quantum Reality, page 64. The following tutorial outlines the origin of de Broglie’s wave hypothesis for matter and how it transforms classical kinetic energy into quantum mechanical confinement energy.
Wave-Particle Duality
Wave-particle duality as expressed in the de Broglie equation is the foundational concept of quantum theory. The mathematical form of de Broglie's equation is derived for the photon. It is subsequently assumed that it applies also to matter.
The momentum of a photon is inversely proportional to its wavelength. The derivation begins with Einstein's mass-energy equation which applies in general.
\[E = mc^{2} \xrightarrow[E=h \nu]{p=mc} pc=h \nu \xrightarrow{c= \nu \lambda} p = \frac{h}{\lambda} \nonumber \]
De Broglie postulated that this expression involving the particle property momentum and the wave property wavelength also applies to matter. Therefore the wavelength of a particle is inversely proportional to its momentum. This is the origin of wave-particle duality.
\[\lambda = \frac{h}{m \nu} = \frac{h}{p} \nonumber \]
A wave is spatially delocalized. A particle is spatially localized. These incompatible concepts are united by the de Broglie equation with the wave property (wavelength) on the left and the particle property (momentum) on the right in a reciprocal relationship mediated by the ubiquitous Planck's constant.
The de Broglie equation is a dictionary for translating classical kinetic energy into quantum language. The quantum equivalent of kinetic energy should be called confinement energy because there is no motion; a particle confined to a circular orbit, as in the Bohr model of the hydrogen atom, is in a stationary state. Restrictions are placed on the particle's wavelength (\(n \lambda = 2 \pi R\)) in order to avoid self-interference.
\[T = \frac{p^{2}}{2m} \xrightarrow{p= \frac{h}{\lambda}} \frac{h^{2}}{2m \lambda^{2}} \xrightarrow[n \lambda = 2 \pi R^{2}]{confinement} \frac{n^{2} h^{2}}{8 \pi^{2} mR^{2}} \nonumber \]
We always measure particles (detectors click, photographic film is darkened, etc.), but we interpret what happened or predict what will happen by assuming wavelike behavior. In other words, quantum particles exhibit both wave and particle properties in every experiment. To paraphrase Nick Herbert (Quantum Reality), particles are always detected, but the experimental results observed are the result of wavelike behavior.
In The Character of Physical Law Feynman described wave-particle duality as follows, "I will summarize, then, by saying that electrons arrive in lumps, like particles, but the probability of arrival of these lumps is determined as the intensity of waves would be. It is in this sense that the electron behaves sometimes like a particle and sometimes like a wave. It behaves in two different ways at the same time." Lawrence Bragg summarized wave-particle behavior saying, "Everything in the future is a wave, everything in the past is a particle."
In his 1951 treatise Quantum Theory, David Bohm described wave-particle duality as follows: "One of the characteristic features of quantum theory is wave-particle duality, i.e. the ability of matter or light quanta to demonstrate the wave-like property of interference, and yet to appear subsequently in the form of localizable particles, even after such interference has taken place." In other words, to explain interference phenomena wave properties must be assigned to matter and light quanta prior to detection as particles.
Whenever it is measured the world seems particle-like, but the pattern formed by these particles leads to the conclusion that between measurements the world acts like a wave.
Nothing but particles are ever detected, but the pattern of these (detected) particles must have been caused by some sort of wave - the form light seems to take when it is not being measured.
The following three-slide power-point presentation attempts to provide a concrete illustration of the ideas presented above by Feynman, Bohm, Bragg and Herbert by examining single-slit diffraction through the lense of wave-particle duality.
Wave-particle Duality Illustrated
- Source emits light
- When viewed through a narrow slit interference fringes are observed, the signature of wave-like behavior.
- However, the detector (eye) registers particles (retinal absorbs a photon and changes shape ultimately causing a signal to be sent to the brain via the optic nerve)
- We detect particles, but we predict what will happen, or interpret what happened, by assuming wave-like behavior
- “Everything in the future is a wave, everything in the past is a particle.” Lawrence Bragg
Retinal Absorbs a Photon
Single-slit Diffraction
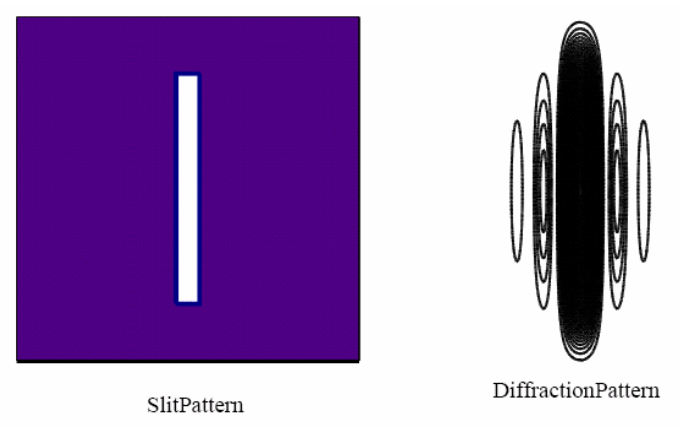
The double-slit diffraction experiment provides an even more dramatic illustration of wave-particle duality in action. Richard Feynman once said that if anyone asks you a question about quantum mechanics, you can always reply "You remember the experiment with the two slits? It's the same thing."
Regarding the double-slit experiment, Feynman also wrote "We choose to examine a phenomenon which is impossible, absolutely impossible, to explain in any classical way, and which has in it the heart of quantum mechanics. In reality, it contains the only mystery. We cannot make the mystery go away by 'explaining' how it works. We will just tell you how it works. In telling you how it works we will have told you about the basic peculiarities of all quantum mechanics.
The stabilities of hydrogen and helium, the most abundant elements in the universe, are now explained using rudimentary quantum principles.
Atomic Stability
Neils Bohr once observed that from the perspective of classical physics the stability of matter was a pure miracle. The problem, of course, is that two of the basic building blocks of matter are oppositely charged - the electron and the proton.Given Coulomb's Law the troubling question is what keeps them from coalescing?
Quantum mechanics is considered by many to be an abstract and esoteric science that doesn't have much to do with everyday life. Yet it provides an explanation for atomic and molecular stability, and classical physics fails at that task. Thus, to achieve some understanding of one of the basic facts about the macro-world requires quantum mechanical concepts and tools.
The issue of atomic stability will be explored with a quantum mechanical analysis of the two simplest elements in the periodic table - hydrogen and helium. They are also the two most abundant elements in the universe. Schrödinger's equation can be solved exactly for the hydrogen atom, but approximate methods are required for the helium atom. In this study, the variational method will be used for both hydrogen and helium.
Variational Method for the Hydrogen Atom
Normalized trial wave function:
\[\Psi (\alpha, r) \colon =\sqrt{\frac{\alpha^{3}}{\pi}} \cdot \exp (- \alpha \cdot r) \nonumber \]
where \(\alpha\) is a scale-factor that controls the size of the wave function.
Integral:
\[\int_{0}^{\infty} \Box \cdot 4 \pi r^{2}\; dr \nonumber \]
Kinetic energy operator:
\[- \frac{1}{2r} \frac{d^{2}}{dr^{2}} (r \cdot \Box) \nonumber \]
Potential energy operator:
\[\frac{-Z}{r} \cdot \Box \nonumber \]
Demonstrate that the trial function is normalized:
\[\int_{0}^{\infty} \Psi (\alpha, r)^{2} \cdot 4 \pi r^{2}\; dr\; \text{assume,}\; \alpha > 0 \rightarrow 1 \nonumber \]
Plot trial wave function for several values of \(\alpha\), the variational parameter:
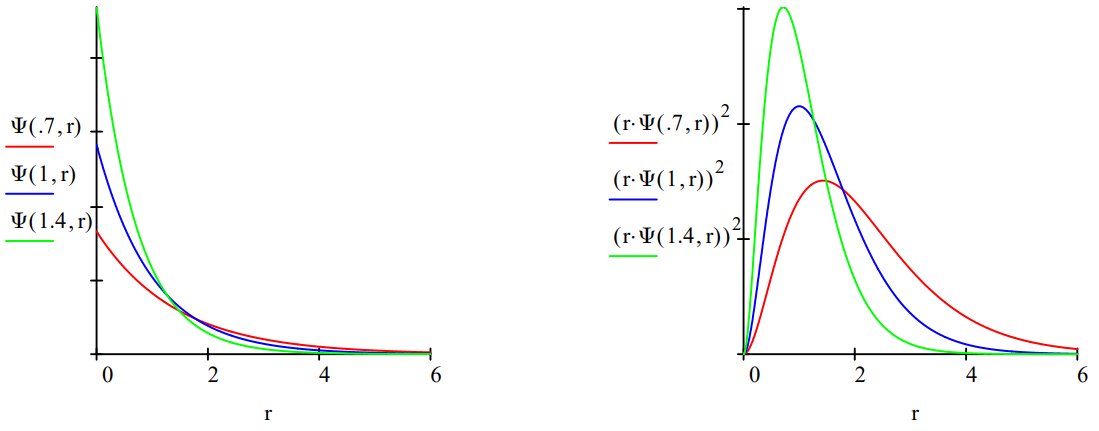
Calculate the average value of the kinetic energy of the electron:
\[T(\alpha) :=\int_{0}^{\infty} \Psi (\alpha, r) \cdot - \frac{1}{2r} \frac{d^{2}}{dr^{2}} (r \cdot \Psi (\alpha, r)) \cdot 4 \pi r^{2}\; dr\; \text{assume,}\; \alpha > 0 \rightarrow \frac{\alpha^{2}}{2} \nonumber \]
Calculate the average value of the potential energy of the electron:
\[V(\alpha, Z) :=\int_{0}^{\infty} \Psi (\alpha, r) \cdot - \frac{Z}{r} \cdot \Psi (\alpha, r) \cdot 4 \pi r^{2}\; dr\; \text{assume,}\; \alpha > 0 \rightarrow -Z \cdot \alpha \nonumber \]
Calculate R, the average distance of the electron from the nucleus:
\[R(\alpha) :=\int_{0}^{\infty} \Psi (\alpha, r) \cdot r \cdot \Psi (\alpha, r) \cdot 4 \pi r^{2}\; dr\; \text{assume,}\; \alpha > 0 \rightarrow \frac{3}{2 \alpha} \nonumber \]
From this we find that:
\[E(\alpha)=T(\alpha)+V(\alpha, Z) = \frac{\alpha^{2}}{2} - \alpha \cdot Z \nonumber \]
But from above we know:
\[\alpha = \frac{3}{2R} \nonumber \]
This allows us to express the total energy and its components in terms of R the average distance of the electron from the nucleus.
Total energy:
\[E(R,Z) \colon =\frac{\alpha^{2}}{2} - \alpha \cdot Z |_{\text{expand}}^{\text{substitute,}\; \alpha = \frac{3}{2R}} \rightarrow \frac{9}{8R^{2}} - \frac{3Z}{2R} \nonumber \]
Electron kinetic energy:
\[T_{E}(R) \colon =\frac{9}{8R^{2}} \nonumber \]
Electron-nucleus potential energy:
\[V_{NE}(R,Z) \colon =\frac{-3Z}{2R} \nonumber \]
E, TE and VNE are graphed versus R for the hydrogen atom (Z=1):
\[R \colon =0, 0.01, \ldots 8 \nonumber \]
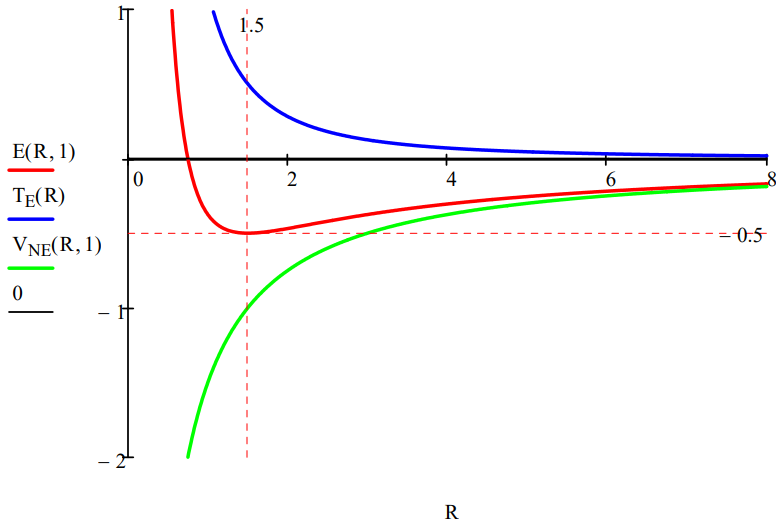
The hydrogen atom ground-state energy is determined by minimizing its energy with respect to R:
\[R \colon =R \qquad R \colon =\frac{d}{dR} E(R,1) = 0\; \text{solve,}\; R \rightarrow \frac{3}{2} \qquad E(R,1)=-0.5 \nonumber \]
Imagine a hydrogen atom forming as an electron approaches a proton from a great distance. The electron is drawn toward the proton by the Coulombic attractive interaction between the two opposite charges and the potential energy decreases like -1/R. The attractive potential energy interaction confines the electron to a smaller volume and the kinetic energy increases as 1/R2. Thus the kinetic energy goes to positive infinity faster than the potential energy goes to negative infinity and a total energy minimum (ground state) is achieved at R = 1.5, as shown in the figure above.
The electron does not collapse into (coalesce with) the proton under the influence of the attractive Coulombic interaction because of the repulsive effect of the confinement energy - that is, kinetic energy. Kinetic energy, therefore, is at the heart of understanding atomic stability.
Variational Method for the Helium Atom
Now we will proceed to the He atom. There are five contributions to the total electronic energy: kinetic energy of each electron, the interaction of each electron with the nucleus, and the electron-electron interaction.The only new term is the last, electron-electron potential energy. It is evaluated as follows for two electrons in 1s orbitals.
The electrostatic potential at r due to electron 1 is:
\[\Phi (\alpha, r) \colon = \frac{1}{r} \int_{0}^{r} \Psi (\alpha, x)^{2} 4 \pi x^{2}\; dx + \int_{r}^{\infty} \frac{\Psi (\alpha, x)^{2} 4 \pi x^{2}}{x} dx \Bigg|_{\text{simplify}}^{\text{assume,}\; \alpha > 0} \rightarrow \frac{e^{-2 \alpha r} + \alpha re^{-2 \alpha r} - 1}{r} \nonumber \]
The electrostatic interaction between the two electrons is:
\[V_{EE} \colon \int_{0}^{\infty} \Phi (\alpha, r) \Psi (\alpha, r)^{2} 4 \pi r^{2}\; dr \Bigg|_{\text{simplify}}^{\text{assume,}\; \alpha > 0} \rightarrow \frac{5 \alpha}{8} \nonumber \]
In terms of R, the electron-electron potential energy is:
\[V_{EE}(R) \colon = \frac{15}{16R} \nonumber \]
\[Z \colon = 2 \qquad E_{He}(R) \colon = (R) 2 T_{E} (R) + 2 V_{NE}(R,Z) + V_{EE}(R) \qquad V(R) \colon = 2 V_{NE}(R,Z) + V_{EE}(R) \nonumber \]
The various contributions to the total electronic energy of the helium atom are plotted below.
\[R \colon = 0, 0.01 \ldots 4 \nonumber \]
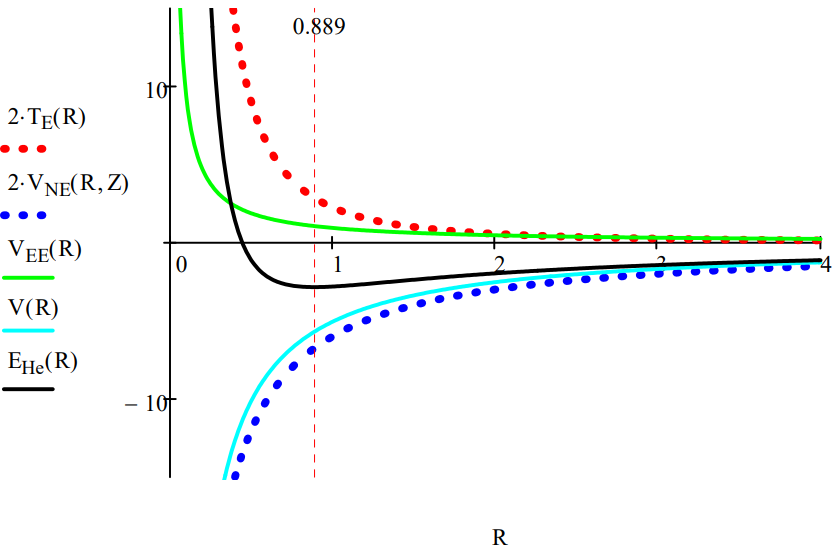
The helium atom ground-state energy is determined by minimizing its energy with respect to R:
\[R \colon =R \qquad R \colon =\frac{d}{dR} E_{He}(R) = 0\; \text{solve,}\; R \rightarrow \frac{8}{9} \qquad R = 0.889 \qquad E_{He}(R)=-2.848 \nonumber \]
Graphing EHe vs. <R> reveals again that kinetic energy (confinement energy) is the key to atomic stability. Several things should be noted in the graph shown above. First, that when the total energy minimum is achieved VNE and V (VNE + VEE) are still in a steep decline. This is a strong indication that VEE is really a rather feeble contribution to the total energy, increasing significantly only long after the energy minimum has been attained. Thus electron-electron repulsion cannot be used to explain atomic stability. The graph above clearly shows that on the basis of classical electrostatic interactions, the electron should collapse into the nucleus. This is prevented by the kinetic energy term for the same reasons as were given for the hydrogen atom.
Unfortunately chemists give too much significance to electron-electron repulsion (VSEPR for example) when it is really the least important term in the Hamiltonian energy operator. And to make matters worse they completely ignore kinetic energy as an important factor in atomic and molecular phenomena. It is becoming increasing clear in the current literature that many traditional explanations for chemical phenomena based exclusively on electrostatic arguments are in need of critical re-examination.
Scientists work almost exclusively in coordinate space when they do quantum calculations. There are two other options, momentum space and phase space, as the following tutorial shows. Calculations on the hydrogen atom are provided for all three computational venues in the following box.
Quantum Calculations on the Hydrogen Atom in Coordinate, Momentum and Phase Space
Coordinate Space Operators
| Position operator | \(x \cdot \Box\) |
| Momentum operator | \(p = \frac{1}{i} \frac{d}{dx} \Box\) |
| Integral | \(\int_{0}^{\infty} \Box \; dx\) |
| Kinetic energy operator | \(KE = - \frac{1}{2} \frac{d^{2}}{dx^{2}} \Box\) |
| Potential energy operator | \(PE= \frac{-1}{x} \cdot \Box\) |
The energy operator for the one‐dimensional hydrogen atom in atomic units is:
\[\frac{-1}{2} \frac{d^{2}}{dx^{2}} \Box - \frac{1}{x} \Box \nonumber \]
The ground state wave function in coordinate space is:
\[\Psi (x) \colon = 2 \cdot x \cdot \exp (-x) \nonumber \]
Display the coordinate‐space distribution function:
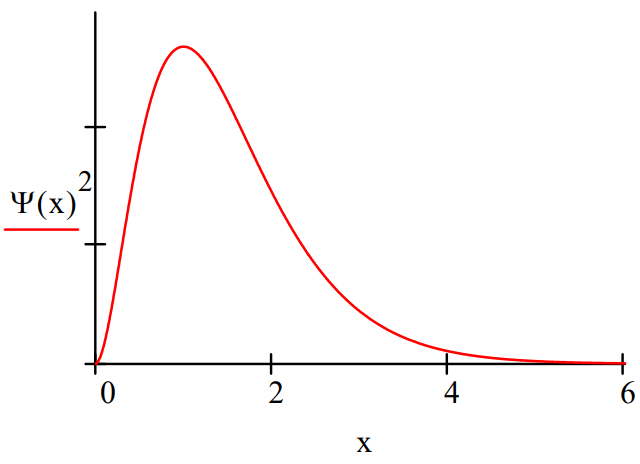
The ground state energy is ‐0.5 Eh.
\[\frac{-1}{2} \frac{d^{2}}{dx^{2}} \Psi (x) - \frac{1}{x} \Psi (x) = E \cdot \Psi (x)\; \text{solve,} \; E \rightarrow \frac{-1}{2} \nonumber \]
| The coordinate wave function is normalized | \(\int_{0}^{\infty} \Psi (x)^{2} \; dx = 1\) |
| The expectation value for position | \(\int_{0}^{\infty} x \cdot \Psi (x)^{2} \; dx = 1.5\) |
| The expectation value for momentum | \(\int_{0}^{\infty} \Psi (x) \cdot \frac{1}{i} \frac{d}{dx} \Psi (x) \; dx = 0\) |
| The expectation value for kinetic energy | \(\int_{0}^{\infty} \Psi (x) \cdot \frac{-1}{2} \frac{d^{2}}{dx^{2}} \Psi (x) \; dx = 0.5\) |
| The expectation value for potential energy | \(\int_{0}^{\infty} \frac{-1}{x} \cdot \Psi (x)^{2} \; dx = -1\) |
The momentum wave function is generated by the following Fourier transform of the coordinate space wave function.
\[\Phi (p) \colon = \frac{1}{\sqrt{2 \pi}} \int_{0}^{\infty} \exp(-ipx) \cdot \Psi (x)\; dx \rightarrow \frac{2^{1/2}}{\pi^{1/2} \cdot (ip + 1)^{2}} \nonumber \]
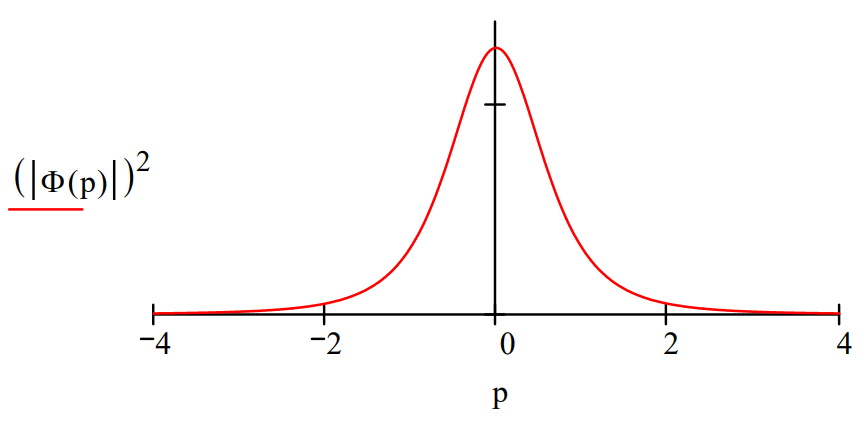
Momentum Space Operators
| Momentum space integral | \(\int_{- \infty}^{\infty} \Box \; dp\) |
| Momentum operator | \(p \cdot \Box\) |
| Kinetic energy operator | \(\frac{p^{2}}{2}\) |
| Position operator | \(i \cdot \frac{d}{dp} \Box\) |
The same calculations made with the momentum space wave function:
| The coordinate wave function is normalized | \(\int_{- \infty}^{\infty} (| \Phi (p)|)^{2}\; dp = 1\) |
| The expectation value for position | \(\int_{- \infty}^{\infty} \overline{\Phi (p)} \cdot i \cdot \frac{d}{dp} \Phi (p)\; dp = 1.5\) |
| The expectation value for momentum | \(\int_{- \infty}^{\infty} p \cdot (| \Phi (p)|)^{2}\; dp = 0\) |
| The expectation value for kinetic energy | \(\int_{- \infty}^{\infty} \frac{p^{2}}{2} \cdot (| \Phi (p)|)^{2}\; dp = 0.5\) |
| The expectation value for potential energy |
The Wigner function for the hydrogen atom ground state is generated using the momentum wave function.
\[W(x,p) \colon = \frac{1}{2 \pi} \int_{- \infty}^{\infty} \overline{\Phi (p + \frac{s}{2})} \cdot \exp (-isx) \cdot \Phi (p- \frac{s}{2})\; ds \nonumber \]
The Wigner distribution is displayed graphically.
\[N \colon = 60 \quad i \colon = 0 \ldots N \quad x_{i} \colon = \frac{6i}{N} \quad j \colon = 0 \ldots N \quad p_{j} \colon = -5 + \frac{10 \cdot j}{N} \quad Wigner_{i,j} \colon = W(x_{i}, p_{j}) \nonumber \]
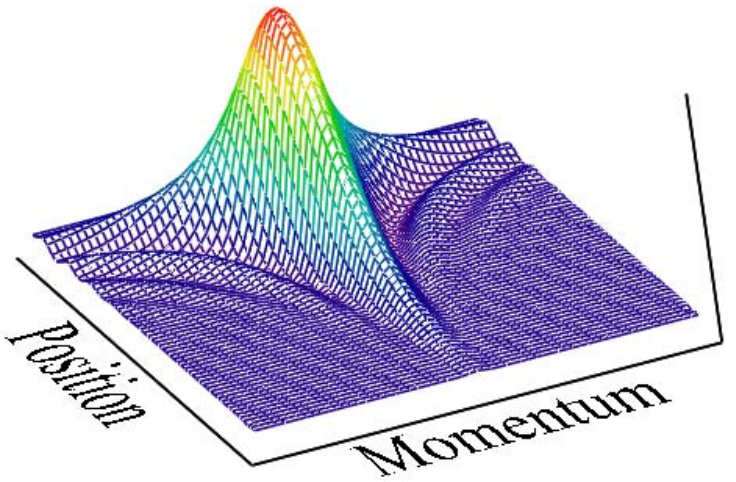
One of the interesting features of doing quantum mechanics with the Wigner distribution is that the position and momentum operators retain their classical forms; they are both multiplicative operators. By comparison in the coordinate representation position is multiplicative and momentum is differential. In the momentum representation itʹs the reverse. This is illustrated below with the following calculations.
| Phase space integral | \(\int_{- \infty}^{\infty} \int_{0}^{\infty} \Box \; dx \; dp\) |
| Position operator | \(x \cdot \Box\) |
| Momentum operator | \(p \cdot \Box\) |
| Kinetic energy operator | \(KE = \frac{p^{2}}{2} \cdot \Box\) |
| Potential energy operator | \(PE = \frac{-1}{x} \cdot \Box\) |
Phase space calculations using the Wigner distribution:
| The Wigner distribution is normalized | \(\int_{- \infty}^{\infty} \int_{0}^{\infty} W(x,p) \; dx \; dp = 1\) |
| The expectation value for position | \(\int_{- \infty}^{\infty} \int_{0}^{\infty} x \cdot W(x,p) \; dx \; dp = 1.5\) |
| The expectation value for momentum | \(\int_{- \infty}^{\infty} \int_{0}^{\infty} p \cdot W(x,p) \; dx \; dp = 0\) |
| The expectation value for kinetic energy | \(\int_{- \infty}^{\infty} \int_{0}^{\infty} \frac{p^{2}}{2} \cdot W(x,p) \; dx \; dp = 0.5\) |
| The expectation value for potential energy | \(\int_{- \infty}^{\infty} \int_{0}^{\infty} \frac{-1}{x} \cdot W(x,p) \; dx \; dp = -1\) |
The phase space calculations require the Wigner distribution function. This link provides further information about the Wigner distribution and how it repackages quantum weirdness.

