20.1: Energy Does not Determine Spontaneity
- Page ID
- 13714
There are many spontaneous events in nature. If you open the valve in both cases a spontaneous event occurs. In the first case the gas fills the evacuated chamber, in the second the gases will mix. The state functions \(U\) and \(H\) do not give us a clue what will happen. You might think that only those events are spontaneous that produce heat.
Not so:
- If you dissolve \(\ce{KNO3}\) in water, it does so spontaneously, but the solution gets cold.
- If you dissolve \(\ce{KOH}\) in water, it does so spontaneously, but the solution gets hot.
Clearly the first law is not enough to describe nature.
Two items left on our wish list
The development of the new state function entropy has brought us much closer to a complete understanding of how heat and work are related:
- the spontaneity problem
- we now have a criterion for spontaneity for isolated systems
- the asymmetry between work->heat (dissipation) and heat->work (power generation)
- at least we can use the new state law to predict the limitations on the latter.
Two problems remain:
- we would like a spontaneity criterion for all systems (not just isolated ones)
- we have a new state function \(S\), but what is it?
Entropy on a microscopic scale
Let us start with the latter. Yes we can use S to explain the odd paradox between w and q both being forms energy on the one hand, but the conversion being easier in one direction than the other, but we have introduced the concept entropy purely as a phenomenon on iis own. Scientifically there is nothing wrong with such a phenomenological theory except that experience tells us that if you can understand the phenomenon itself better your theory becomes more powerful.
To understand entropy better we need to leave the macroscopic world and look at what happens on a molecular level and do statistics over many molecules. First, let us do a bit more statistics of the kind we will need.
Permutations
If we have n distinguishable objects, say playing cards we can arrange them in a large number of ways. For the first object in our series we have \(n\) choices, for number two we have \(n-1\) choices (the first one being spoken for) etc. This means that in total we have
\[W=n(n-1)(n-2)….4.3.2.1 = n!\;\text{ choices.} \nonumber \]
The quantity \(W\) is usually called the number of realizations in thermodynamics.
The above is true if the objects are all distinguishable. If they fall in groups within which they are not distinguishable we have to correct for all the swaps within these groups that do not produce a distinguishably new arrangement. This means that \(W\) becomes \(\frac{n!}{a!b!c!…z!}\) where a,b, c to z stands for the size of the groups. (Obviously \(a+b+c+..+z = n\))
In thermodynamincs our 'group of objects' is typically an ensemble of systems, think of size Nav and so the factorial become horribly large. This makes it necessary to work with logarithms. Fortunately there is a good approximation (by Stirling) for a logarithmic factorial:
\[\ln N! \approx N \ln N-N \nonumber \]
In Europe nosey little children who are curious to find out where their newborn little brother or sister came from, often get told that the stork brought it during the night. When you look at the number of breeding pairs of this beautiful bird in e.g. Germany since 1960 you see a long decline to about 1980 when the bird almost got extinct. After that the numbers go up again due to breeding programs mostly. The human birth rate in the country follows a pretty much identical curve and the correlation between the two is very high (>0.98 or so). (Dr H. Sies in Nature (volume 332 page 495; 1988). Does this prove that storks indeed bring babies?

Answer:
No, it does not show causality, just a correlation due a common underlying factor. In this case that is the choices made by the German people. First they concentrated on working real hard and having few children to get themselves out of the poverty WWII had left behind and neglected the environment, then they turned to protect the environment and opened the doors to immigration of people, mostly from Muslim countries like Turkey or Morocco, that usually have larger families. The lesson from this is that you can only conclude causality if you are sure that there are no other intervening factors.
Changing the size of the box with the particles in it
The expansion of an ideal gas against vacuum is really a wonderful model experiment, because nothing else happens but a spontaneous expansion and a change in entropy. No energy change, no heat, no work, no change in mass, no interactions, nothing. In fact, it does not even matter whether we consider it an isolated process or not. We might as well do so.
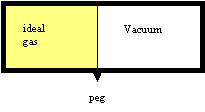
Physicists and Physical Chemists love to find such experiments that allows them to retrace causality. All this means that if we look at what happens at the atomic level, we should be able to retrace the cause of the entropy change. As we have seen before, the available energy states of particles in a box depend on the size of the box.
\[ E_{kin} = \dfrac{h^2}{8ma^2} \left[ n_1^2 + n_2^2 + n_2^2 \right] \nonumber \]
Clearly if the side (\(a\) and therefore the volume of the box changes, the energy spacing between the states will become smaller. Therefore during our expansion against vacuum, the energy states inside the box are changing. Because \(U\) does not change the average energy \(\langle E \rangle\) is constant. Of course this average is taken over a great number of molecules (systems) in the gas (the ensemble), but let's look at just two of them and for simplicity let us assume that the energy of the states are equidistant (rather than quadratic in the quantum numbers n).
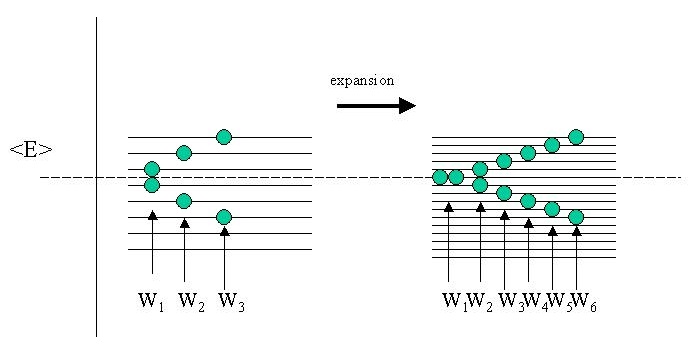
As you can see there is more than one way to skin a cat, or in this case to realize the same average \(\langle E \rangle\) of the complete ensemble (of only two particles admittedly). Before expansion I have shown three realizations W1, W2, W3 that add up to the same \(\langle E \rangle\). After expansion however, there are more energy states available and the schematic figure shows twice as many realizations W in the same energy interval.
Boltzmann was the first to postulate that this is what is at the root of the entropy function, not so much the (total) energy itself (that stays the same!), but the number of ways the energy can be distributed in the ensemble. Note that because the ensemble average (or total) energy is identical, we could also say that the various realizations \(W\) represent the degree of degeneracy \(Ω\) of the ensemble.
Boltzmann considered a much larger (canonical) ensemble consisting of a great number of identical systems (e.g. molecules, but it could also be planets or so). If each of our systems already has a large number of energy states the systems can all have the same (total) energy but distributed in rather different ways. This means that two systems within the ensemble can either have the same distribution or a different one. Thus we can divide the ensemble A in subgroups aj having the same energy distribution and calculate the number of ways to distribute energy in the ensemble \(A\) as
\[W= \dfrac{A!}{a1!a2!…}. \nonumber \]
Boltzmann postulated that entropy was directly related to the number of realizations W, that is the number of ways the same energy can be distributed in the ensemble. This leads immediately to the concept of order versus disorder, e.g, if the number of realizations is \(W=1\), all systems must be in the same state (W=A! / A!0!0!0!…) which is a very orderly arrangement of energies.
If we were to add two ensembles to each other the total number of possible arrangements Wtot becomes the product W1W2 but the entropies should be additive. As logarithms transform products into additions Boltzmann assumed that the relation between W and S should be logarithmic and wrote:
\[S= k \ln W \nonumber \]
Again, if we consider a very ordered state, e.g. where all systems are in the ground state the number of realizations A!/A!= 1 so that the entropy is zero. If we have a very messy system where the number of ways to distribute energy over the many many different states is very large S becomes very large. Thus entropy is very large.
This immediately gives us the driving force for the expansion of a gas into vacuum or the mixing of two gases. We simply get more energy states to play with, this increases W. This means an increase in S. This leads to a spontaneous process.

