13.9: Normal Modes in Polyatomic Molecules
- Page ID
- 13672
Normal modes are used to describe the different vibrational motions in molecules. Each mode can be characterized by a different type of motion and each mode has a certain symmetry associated with it. Group theory is a useful tool in order to determine what symmetries the normal modes contain and predict if these modes are IR and/or Raman active. Consequently, IR and Raman spectroscopy is often used for vibrational spectra.
Degrees of Freedom
In general, a normal mode is an independent motion of atoms in a molecule that occurs without causing movement to any of the other modes. Normal modes, as implied by their name, are orthogonal to each other. In order to discuss the quantum-mechanical equations that govern molecular vibrations it is convenient to convert Cartesian coordinates into so called normal coordinates. Vibrations in polyatomic molecules are represented by these normal coordinates.
A molecule can have three types of degrees of freedom and a total of 3N degrees of freedom, where N equals the number of atoms in the molecule. These degrees of freedom can be broken down into three categories.
- Translational: These are the simplest of the degrees of freedom. These entail the movement of the entire molecule’s center of mass. This movement can be completely described by three orthogonal vectors and thus contains 3 degrees of freedom.
- Rotational: These are rotations around the center of mass of the molecule and like the translational movement they can be completely described by three orthogonal vectors. This again means that this category contains only 3 degrees of freedom. However, in the case of a linear molecule only two degrees of freedom are present due to the rotation along the bonds in the molecule having a negligible inertia.
- Vibrational: These are any other types of movement not assigned to rotational or translational movement and thus there are 3N – 6 degrees of vibrational freedom for a nonlinear molecule and 3N – 5 for a linear molecule. These vibrations include bending, stretching, wagging and many other aptly named internal movements of a molecule. These various vibrations arise due to the numerous combinations of different stretches, contractions, and bends that can occur between the bonds of atoms in the molecule.
| Total Degrees of Freedom | Translational degrees of freedom | Rotational degrees of freedom | Vibrational degrees of freedom | |
|---|---|---|---|---|
| Nonlinear Molecules | 3N | 3 | 3 | 3N -6 |
| Linear Molecules | 3N | 3 | 2 | 3N - 5 |
Each of these degrees of freedom is able to store energy. However, In the case of rotational and vibrational degrees of freedom, energy can only be stored in discrete amounts. This is due to the quantized break down of energy levels in a molecule described by quantum mechanics. In the case of rotations the energy stored is dependent on the rotational inertia of the gas along with the corresponding quantum number describing the energy level.
Ethane, \(C_2H_6\) has eight atoms (\(N=8\)) and is a nonlinear molecule so of the \(3N=24\) degrees of freedom, three are translational and three are rotational. The remaining 18 degrees of freedom are internal (vibrational). This is consistent with:
\[3N -6 =3(8)-6=18 \nonumber \]
Carbon Dioxide, \(CO_2\) has three atoms (\(N=3\) and is a linear molecule so of the \(3N=9\) degrees of freedom, three are translational and two are rotational. The remaining 4 degrees of freedom are vibrational. This is consistent with:
\[3N - 5 = 3(3)-5 = 4 \nonumber \]
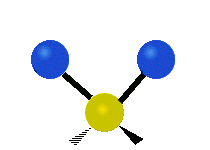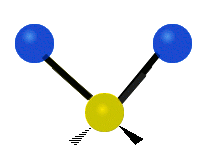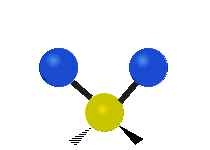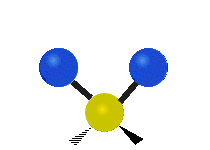
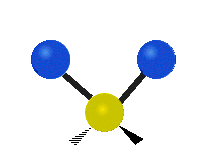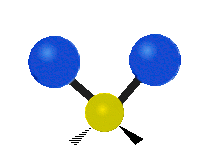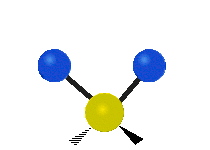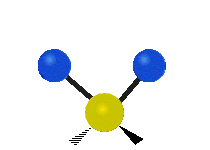
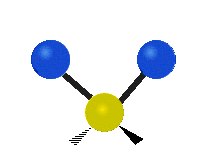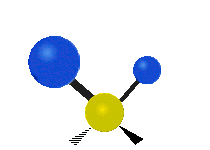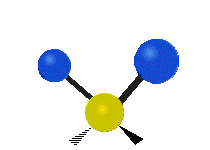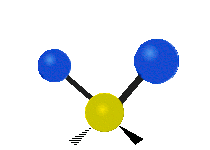
The normal modes of vibration are: asymmetric, symmetric, wagging, twisting, scissoring, and rocking for polyatomic molecules.
| Symmetricical Stretching | Asymmetrical Stretching | Wagging |
 |
 |
 |
| Twisting | Scissoring | Rocking |
 |
 |
 |
Figure 13.9.1 : Six types of Vibrational Modes. Taken from publisher en.Wikipedia.org/wiki/Infrared_spectroscopy with permission from copyright holder.
Normal Modes
If there is no external field present, the energy of a molecule does not depend on its orientation in space (its translational degrees of freedom) nor its center of mass (its rotational degrees of freedom). The potential energy of the molecule is therefore made up of its vibrational degrees of freedom only of \(3N-6\) (or \(3N-5\) for linear molecules). The difference in potential energy is given by:
\[ \begin{align} \Delta V &= V(q_1,q_2,q_3,...,q_n) - V(0,0,0,...,0) \label{1} \\[4pt] &= \dfrac{1}{2} \sum_{i=1}^{N_{vib}} \sum_{j=1}^{N_{vib}} \left(\dfrac{\partial^2 V}{\partial q_i\partial q_j} \right) q_iq_j \label{2} \\[4pt] &= \dfrac{1}{2}\sum_{i=1}^{N_{vib}} \sum_{j=1}^{N_{vib}} f_{ij} q_iq_j \label{3} \end{align} \]
where \(q\) represents the equilibrium displacement and \(N_{vib}\) the number of vibrational degrees of freedom.
For simplicity, the anharmonic terms are neglected in this equation (i.e., higher order terms are ignore). A theorem of classical mechanics states that the cross terms can be eliminated from the above equation (the details of the theorem are very complex and will not be discussed in detail). By using matrix algebra a new set of coordinates {Qj} can be found such that
\[\Delta{V} = \dfrac{1}{2} \sum_{j=1}^{N_{vib}}{F_jQ_j^2} \label{4} \]
Note that there are no cross terms in this new expression. These new coordinates are called normal coordinates or normal modes. With these new normal coordinates in hand, the Hamiltonian operator for vibrations can be written as follows:
\[\hat{H}_{vib} = -\sum_{j=1}^{N_{vib}} \dfrac{\hbar^2}{2\mu_i} \dfrac{d^2}{dQ_j^2} + \dfrac{1}{2} \sum_{j=1}^{N_{vib}}F_jQ_j^2 \label{5} \]
The total wavefunction is a product of the individual wavefunctions and the energy is the sum of independent energies. This leads to:
\[ \hat{H}_{vib} = \sum_{j=1}^{N_{vib}} \hat{H}_{vib,j} = \sum_{j=1}^{N_{vib}} \left( \dfrac{-\hbar^2}{2 \mu_j}\dfrac{d^2}{dQ_i^2} + \dfrac{1}{2}\sum_{j=1}^{N_{vib}} F_jQ_j^2 \right) \label{6} \]
and the wavefunction is then
\[\begin{align*} \psi_{vib} &= Q_1,Q_2, Q_3 ..., Q_{vib} \\[4pt] &= \psi_{vib,1}(Q_1) \psi_{vib,2}(Q_2) \psi_{vib,3}(Q_3) , ..., \psi_{vib,N_{vib}}(Q_{N_{vib}}) \end{align*} \nonumber \]
and the total vibrational energy of the molecule is
\[E_{vib} = \sum_{j=1}^{N_{vin}} h\nu_j \left (v_j + \dfrac{1}{2}\right) \label{8} \]
where \(v_j= 0,1,2,3...\).
The consequence of the result stated in the above equations is that each vibrational mode can be treated as a harmonic oscillator approximation. There are \(N_{vib}\) harmonic oscillators corresponding to the total number of vibrational modes present in the molecule.
Pictorial description of normal coordinates using CO
The normal coordinate \(q\) is used to follow the path of a normal mode of vibration. As shown in Figure 13.9.2 the displacement of the \(\ce{C}\) atom, denoted by \(Δr_o(\ce{C})\), and the displacement of the \(\ce{O}\) atom, denoted by \(Δr_o(\ce{O})\), occur at the same frequency. The displacement of atoms is measured from the equilibrium distance in ground vibrational state, \(r_o\).