26.1: Equilibrium Results when Gibbs Energy is Minimized
- Page ID
- 14522
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Many important chemical reactions -if not most- are performed in solution rather than between solids or gases. Solid state reactions are often very slow and not all chemical species can be put in the vapor phase because they decompose before evaporating.
Often we are not concerned with the temporal aspects of a reaction. That can be technologically very important but it is the domain of kinetics - a different branch of Physical Chemistry - rather than classical thermodynamics.. The latter is more concerned with the endpoint. This is the thermodynamically speaking the (stable) equilibrium, but chemically it can either represent a completed reaction or a chemical equilibrium.
Unfortunately, of the three main aggregation states: gas – liquid – solid, the structure of liquids is least understood and one of the most complex liquids is also one of the most extensively used ones: water. It is vital to many branches of chemistry varying from geochemistry to environmental chemistry to biochemistry. We shall make just a small inroad into its complexity.
Extent of reaction
To describe the progress of a reaction we define the extent of reaction. It is usually denoted by the Greek letter \(ξ\).
Consider a generic reaction:
\[v_AA + v_BB \rightleftharpoons v_YY + v_ZZ \nonumber \]
Using stoichiometry we can define the extent by considering how the number of moles (or molar amounts) of each species changes during the reaction:
reactants
- \(n_A= n_{A,0} - v_A ξ\)
- \(n_B= n_{B,0} - v_B ξ\)
products
- \(n_Y= n_{Y,0} + v_Y ξ\)
- \(n_Z= n_{Z,0} + v_Z ξ\)
The dimension of ξ is [mol] because the stoichiometric coefficients vi are dimensionless integers. If the reaction goes to completion for one of the reactants -the limiting reactant- nA or B=nlimiting will go to zero. If we start with \(n_{limiting}= v_{limiting}\) moles, the value of ξ starts at 0 (no products) and goes to 1 at completion (limiting reactant depleted). When approaching an equilibrium \(ξ\) will not go beyond \(ξ_{eq}\).
Measuring ξ
The extent of reaction is what is the central subject of reaction kinetics. Its value is typically measured as a function of time indirectly by measuring a quantity q that is linearly dependent on ξ(t):
\[q( ξ ) = aξ +b \nonumber \]
Consider the situation at the extremes \(ξ=0\) and \(ξ=1\):
\[q_0= a.0+b= b \nonumber \]
\[q_1= a.1+b= a+b \nonumber \]
\[q_1-q_0= a \nonumber \]
Thus, \(ξ\) can be found from
\[\dfrac{q(t)-q0}{q_1-q_0}=\dfrac{q(t)-b}{a} \nonumber \]
The nature of \(q\) can vary widely from UV/Vis absorption, conductivity, gravimetric to caloric data.
In practice, \(q_0\) at \(ξ=0\) is often hard to observe because it takes time to mix the reactants, particularly in solutions, and q1 at ξ=1 may never be reached if the reaction goes to equilibrium. Nevertheless the values of a and b can often be found from the available data by fitting techniques.
In (equilibrium, static) thermodynamics we are only concerned with the endpoint:
- \(ξ=1\): the reaction runs to completion
- \(ξ=ξ_{eq}\): the react ion goes to a state of chemical equilibrium
Thermodynamic Potentials
As we have seen we can write any change in the Gibbs free energy due to changes in the molar amounts of the species involved in the reaction (at \(T\), \(P\) constant) as:
\[dG =\sum \dfrac{∂G}{∂n_i} dn_i = \sum μ_idn_i \nonumber \]
where \(μ\) is the thermodynamic potential, often called chemical potential when dealing with reactions. From the definition of ξ we can see by differentiation that
- \(d n_A=- v_Adξ\)
- \(d n_B=- v_Adξ\)
- \(d n_Y= v_Ydξ\)
- \(d n_Z= v_Zdξ\)
This allows us to unify the changes in the molar amount of all the species into one single variable \(dξ\). We get:
\[dG = \left[ \sum -v_{i,reactants} μ_{i,reactants} + \sum+v_{i,products} μ_{j,products} \right]dξ \nonumber \]
or
\[ \left (\dfrac{∂G}{∂ξ} \right)_{T,P} = -\sum v_{i,r}μ_{i,r}+ \sum v_{i,p}μ_{j,p} \nonumber \]
This quantity is also written as:
\[ \left( \dfrac{∂G}{∂ξ} \right)_{T,P} =Δ_rG \nonumber \]
This quantity gives the change in Gibbs free energy for the reaction (as written!!) for Δξ=1 mole. (Units are [J/mol] therefore). This is the change in Gibbs energy (the slope of \(G\) vs \(\xi\)) when the extent of reaction changes by one mole with a fixed composition. Equilibrium results when Gibbs energy is at a minimum with respect to the extent of reaction.
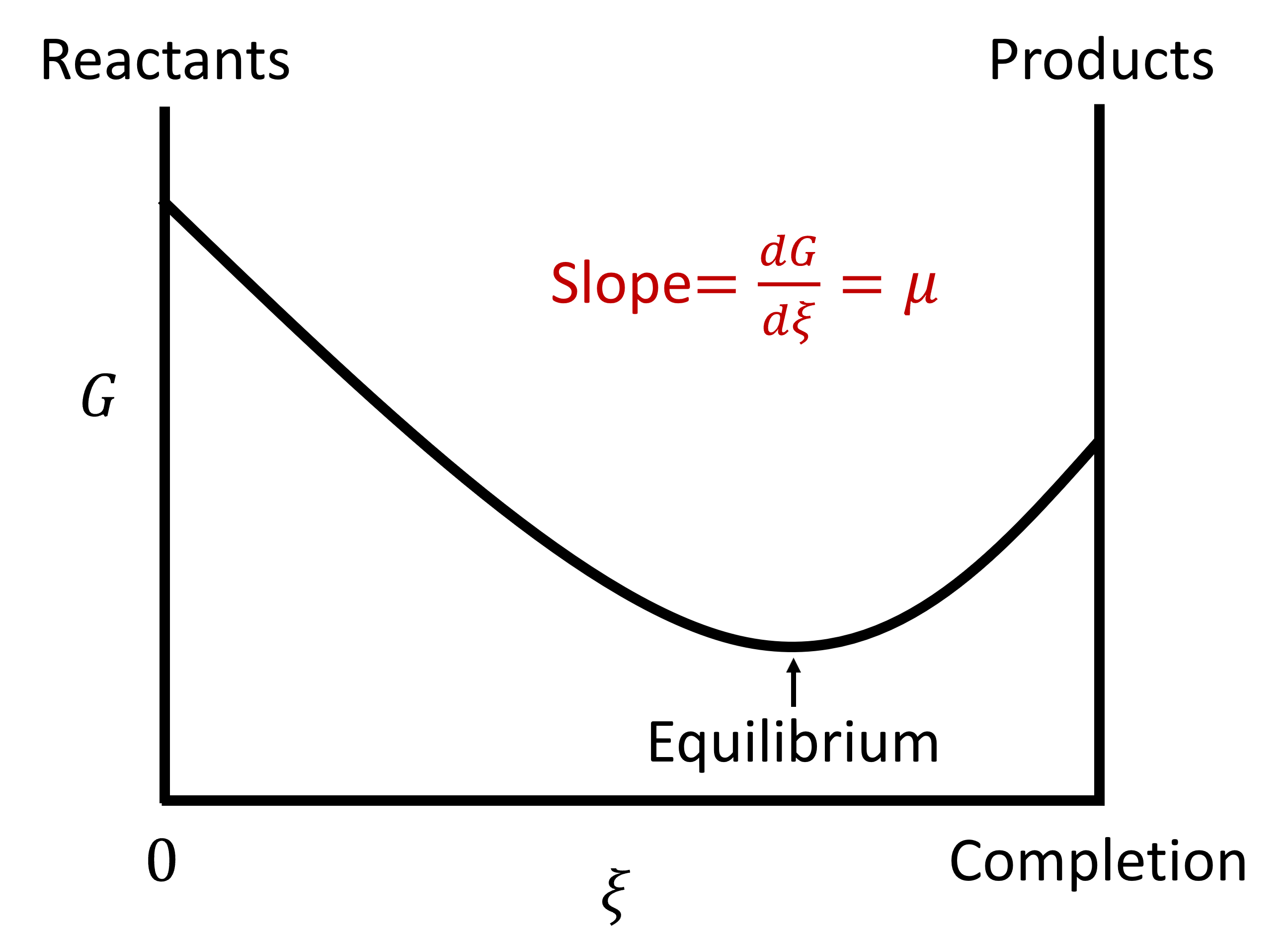
Gas Reactions
Let us assume that our reaction is entirely between gas species and that the gas is sufficiently dilute that we can use the ideal gas law. Then we can write for each species:
\[μ_i= μ_i^o+RT \ln \dfrac{P_i}{P_i^o} \nonumber \]
We can then split up the ΔrG expression in two parts:
\[Δ_rG = Δ_rG^o + RT\ln Q \nonumber \]
The standard potentials:
\[Δ_rG^o = -\sum v_i,_r μ^o_{i,r} + \sum v_{i,p} μ^o_{j,p} \nonumber \]
and the logarithmic terms:
\[RT \ln Q= - v_A RT \ln \left( \dfrac{P_A}{P_A^o} \right)- v_B RT\ln \left( \dfrac{P_B}{P_B^o} \right) + v_YRT \ln \left( \dfrac{P_Y}{P_Y^o} \right) + v_ZRT \ln \left( \dfrac{P_Z}{P_Z^o} \right) \nonumber \]
We can combine all the logarithmic terms into Q, called the reaction quotient. The stoichiometric coefficients become exponents and the reactants' factors will be 'upside down' compared to the products, because of the properties of logarithms:
\[a \ln x = \ln x^a \nonumber \]
\[- a \ln x = \ln \left( \dfrac{1}{x^a} \right) \nonumber \]
We have kept the standard pressures \(P_i^o\) in the expression, but often they are omitted. They are usually all 1 bar, but in principle we could choose 1 bar for A 1 Torr for B an 1 psi for the products. It creates a valid (though ridiculous) definition of what o stands for. (Of course the value of \(Δ_rG^o\) does depend on that choice!).
We could write
\[RT \ln Q = RT \ln \dfrac{Q_P}{Q^o} \nonumber \]
\(Q^o\) is typically unity in magnitude but it cancels the dimensions of \(Q_P\). That means that \(Q\) and \(Q_P\) are equal in magnitude and we can get \(Q\) from \(Q_P\) by simply dropping the dimensions. \(Q\) is dimensionless but \(Q_P\) usually is not. Often this fine distinction is simply not made and \(Q^o\) is omitted, we get:
\[Δ_rG = Δ_rG^o + RT\ln \dfrac{P_Y^{v_Y}P_Z^{v_Z} }{P_A^{v_A}P_B^{v_B}} \nonumber \]
Notice the difference between \(Δ_rG\) which denotes the conditions (e.g. pressures) of your reaction and \(Δ_rG^o\) denotes standard conditions.

