21.5: Practical Absolute Entropies Can Be Determined Calorimetrically
- Page ID
- 14482
From section 21.1, we learned that the entropy at constant pressure changes with temperature by:
\[\Delta S=\int_{T_1}^{T_2}{\frac{C_P(T)}{T}dT} \nonumber \]
From section 21.3, we learned that the entropy of a phase transition is:
\[\Delta_{trs} S=\frac{\Delta_{trs}H}{T_{trs}} \nonumber \]
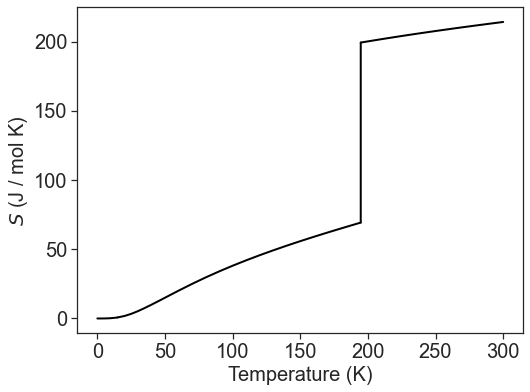
Both the heat capacity and enthalpy of transition can be experimentally determined using calorimetry. Using experimental values with the two above expressions and the convention that the entropy at absolute zero (0 K) is zero, we can calculate the practical absolute entropy of a substance for any temperature. For example, the entropy of CO2 gas at 300 K can be calculated by:
\[S(T)=\int_{0 K}^{T_{sub}}{\frac{C_P^s(T)}{T}dT}+\frac{\Delta_{sub}H}{T_{sub}}+\int_{T_{sub}}^{300\text{ K}}{\frac{C_P^g(T)}{T}dT} \nonumber \]
Where the temperature of sublimation (\(T_{sub}\)) is 194.7 K.