19.5: An Adiabatic Process is a Process in which No Energy as Heat is Transferred

Isothermal expansion of an ideal gas

For a monatomic ideal gas we have seen that energy \(\langle E \rangle\) observed as \(U= 3/2 nRT\). This means that energy is only dependent on temperature and if a gas is compressed isothermally, then the internal energy does not change:

\[ΔU_{isothermal-ideal gas} = 0 \nonumber \]

This means that the reversible work must cancel the reversible heat:

\[ΔU_{rev} = w_{rev} + q_{rev} = 0 \nonumber \]

Therefore

\[w_{rev} = - q_{rev} \nonumber \]

so from the expression of the reversible work for expansion in the last section

\[ q_{rev}= nRT\ln \dfrac{V_2}{V_1} \nonumber \]

If \(V_2>V_1\) (expansion), then you (or the environment) must put heat into the system because this is a positive number.

Adiabatic expansion of an ideal gas

Now suppose you make sure that no heat can enter the cylinder. (Put it in styrofoam or so). Then the path can still be reversible (slow pulling) but the process is then adiabatic.

This bat- part comes from a Greek verb βαινω (baino) that means walking, compare acrobat, someone who goes high places (acro-). The δια (dia) part means 'through' (cf. diagram, diorama, diagonal etc.) and the prefix α- (a-) denies it all (compare atypical versus typical).

So the styrofoam prevents the heat from walking through the wall. When expanding the gas from V₁ to V₂ it still does reversible work but where does that come from? It can only come from the internal energy itself. So in this case any energy change should consist of work (adiabatic means: \(δq=0\)).

\[dU = δw_{rev} \nonumber \]

This implies that the temperature must drop, because if \(U\) changes, then \(T\) must change.

The change of energy with temperature at constant volume is known as the heat capacity (at constant volume) \(C_v\)

\[ C_v =\left( \dfrac{\partial U}{\partial T} \right)_V \nonumber \]

For an ideal gas \(U\) only changes with temperature, so that

or:

We can now compare two paths to go from state \(P_1,V_1,T_1\) to state \(P_2,V_2,T_1\):

1. Reversible isothermal expansion A
2. Reversible adiabatic expansion B followed by reversible isochoric heating C

Figure __:

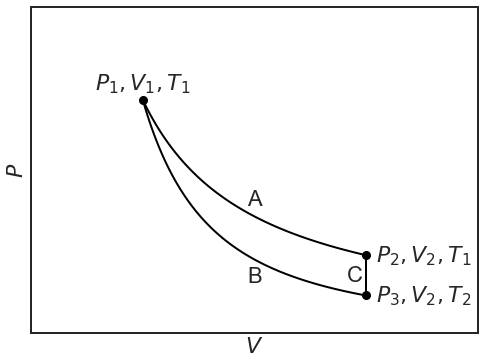
Notice that the temperature remains \(T_1\) for path A (isotherm!), but that it drops to \(T_2\) on the adiabat B, so that the cylinder has to be isochorically warmed up, C, to regain the same temperature.

\(\Delta U_{tot}\) should be the same for both path A and the combined path B+C, because the end points are the same (\(U\) is a state function!). As the and points are at the same temperature and \(U\) only depends on \(T\):

\[\Delta U_{tot}=0 \nonumber \]

Along adiabat B:

\[q_{rev}=0 \nonumber \]

Along isochoric heating C, there is no volume work because the volume is kept constant, so that:

This is the only reversible heat involved in path B+C. However, we know that \(\Delta U_{tot}\) for path A is zero (isothermal!). This means that the volume work along B must cancel the heat along C:

The book keeping looks as follows, all paths are reversible:

\[\Delta U_{B+C} = \Delta U_A = 0 = q_B + w_B + q_C + w_C \nonumber \]

We know that \(q_B=0\) since it is an adiabat and \(w_C=0\) since it is an isochore:

\[\Delta U_{B+C} = \Delta U_A = 0 = 0 + w_B + q_C + 0 \nonumber \]

Therefore:

\[w_B=-q_C \nonumber \]

We had already seen before that along the isotherm A:

\[w_A = - q_A = - nRT \ln \dfrac{V_1}{V_2} \nonumber \]

As you can see \w_A\) and \(w_B\) are not the same. Work is a path function, even if reversible. As we are working with an ideal gas we can be more precise about \(w_B\) and \(q_c\) as well. The term \(w_B\) along the adiabat is reversible volume work. Since there is no heat along B we can write a straight \(d\) instead of \(\delta\) for the work contributions (It is the only contribution and must be identical to the state function \(dU\)):