14.8: The n+1 Rule Applies Only to First-Order Spectra
- Page ID
- 13643
The (n+1) Rule, an empirical rule used to predict the multiplicity and, in conjunction with Pascal’s triangle, splitting pattern of peaks in 1H and 13C NMR spectra, states that if a given nucleus is coupled (see spin coupling) to n number of nuclei that are equivalent (see equivalent ligands), the multiplicity of the peak is n+1. eg. 1:
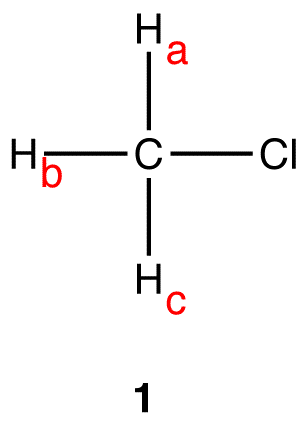
The three hydrogen nuclei in 1, \(H_a\), \(H_b\), and \(H_c\), are equivalent. Thus, 1H NMR spectrum of 1 \(H_a\)s only one peak. \(H_a\), \(H_b\), and \(H_c\) are coupled to no hydrogen nuclei. Thus, for \(H_a\), \(H_b\), and \(H_c\), n=0; (n+1) = (0+1) = 1. The multiplicity of the peak of \(H_a\), \(H_b\), and \(H_c\) is one. The peak \(H_a\)s one line; it is a singlet. eg. 2:
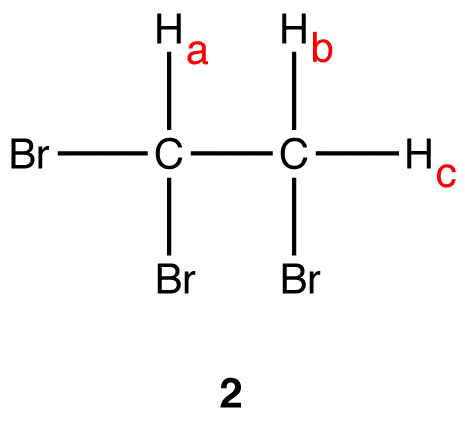
There are two sets of equivalent hydrogen nuclei in 2:
- Set 1: \(H_a\)
- Set 2: \(H_b\), \(H_c\)
Thus, the 1H NMR spectrum of 2 \(H_a\)s two peaks, one due to \(H_a\) and the other to \(H_b\) and \(H_c\).
The peak of \(H_a\): There are two vicinal hydrogens to \(H_a\): \(H_b\) and \(H_c\). \(H_b\) and \(H_c\) are equivalent to each other but not to \(H_a\). Thus, for \(H_a\), n=2; (n+1) = (2+1) = 3. The multiplicity of the peak of \(H_a\) is three. The peak \(H_a\)s three lines; from the Pascal’s triangle, it is a triplet.
The peak of \(H_b\) and \(H_c\): There is only one vicinal hydrogen to \(H_b\) and \(H_c\): \(H_a\). \(H_a\) is not equivalent to \(H_b\) and \(H_c\). Thus, for \(H_b\) and \(H_c\), n=1; (n+1) = (1+1) = 2. The multiplicity of the peak of \(H_b\) and \(H_c\) is two. The peak \(H_a\)s two lines, from the Pascal’s triangle, it is a doublet.
To determine the multiplicity of a peak of a nucleus coupled to more than one set of equivalent nuclei, apply the (n+1) Rule independently to each other.
eg:
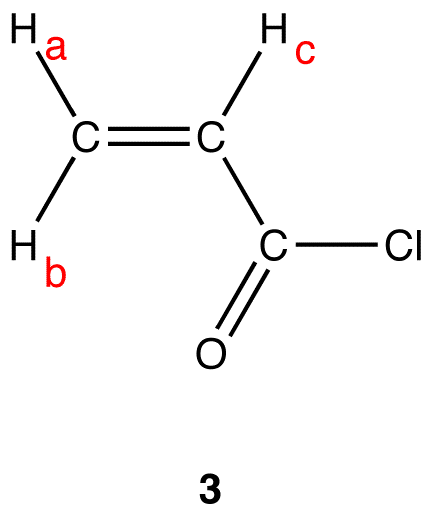
There are three set of equivalent hydrogen nuclei in 3:
- Set 1: \(H_a\)
- Set 2: \(H_b\)
- Set 3: \(H_c\)
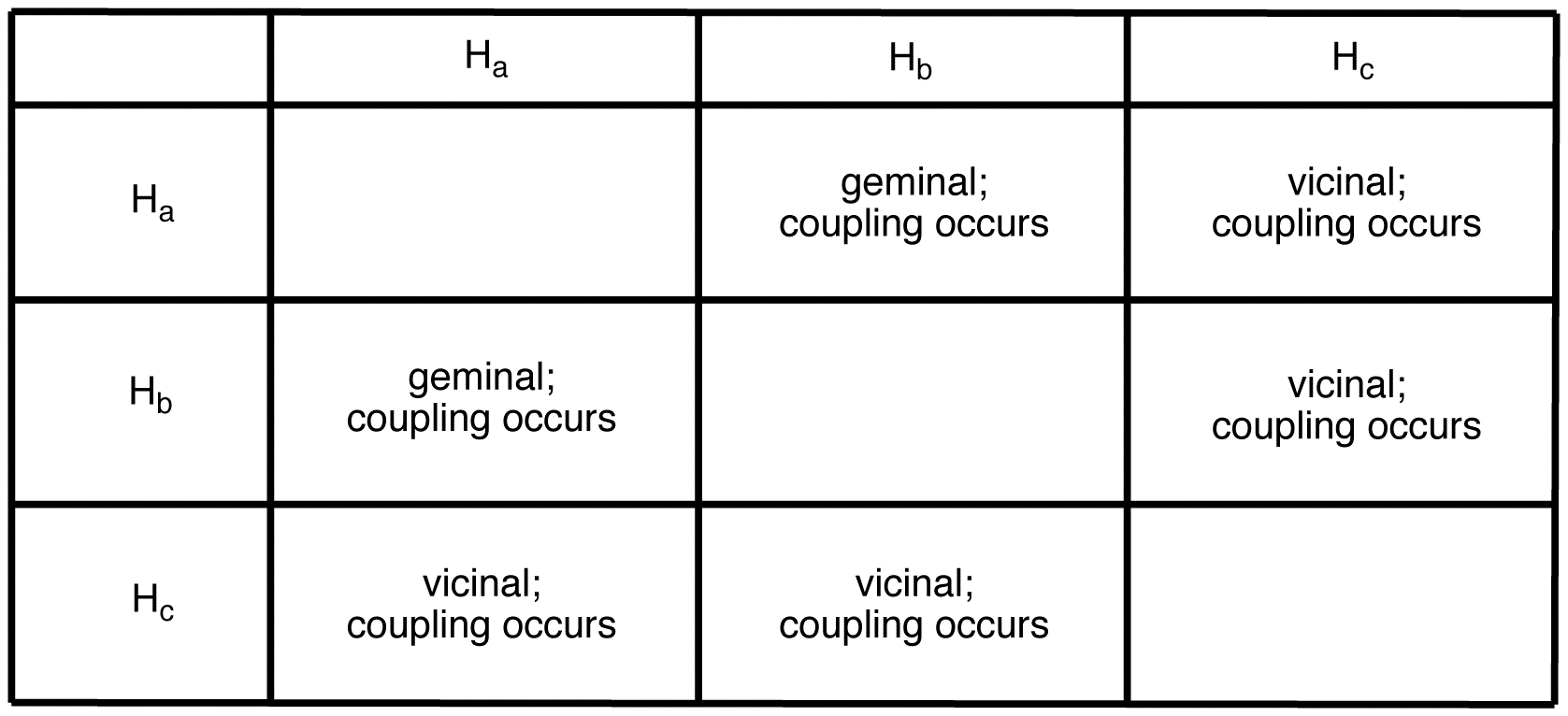
peak of \(H_a\):
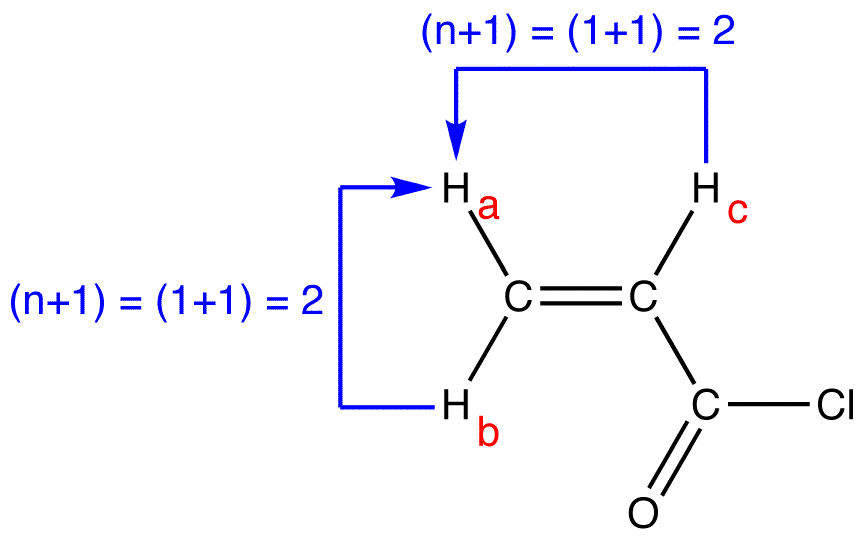
multiplicity of the peak of \(H_a = 2 \times 2 = 4\). To determine the splitting pattern of the peak of \(H_a\), use the Pascal’s triangle, based on the observation that, for alkenyl hydrogens, \(J_{cis} > J_{gem}\).
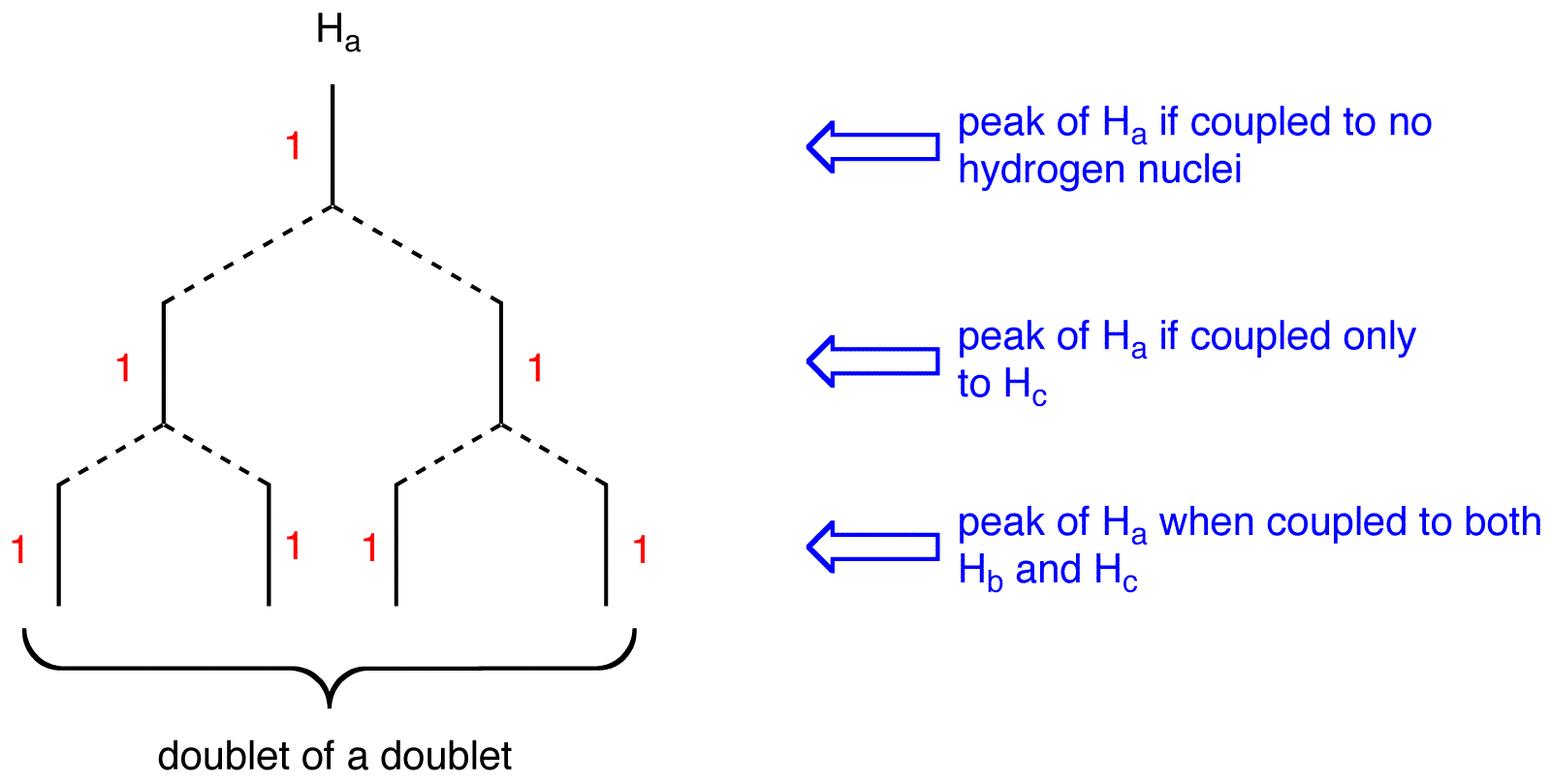
The peak of \(H_a\) is a doublet of a doublet.
peak of \(H_b\):
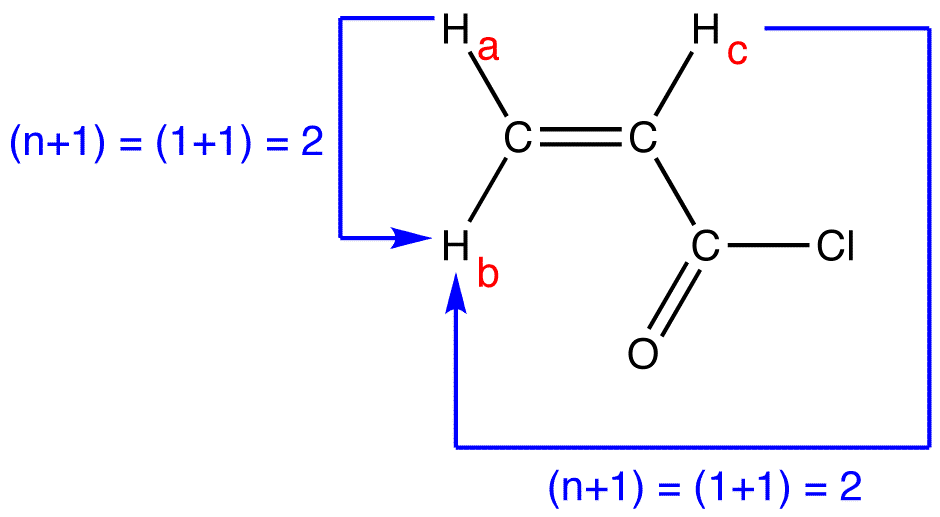
multiplicity of the peak of \(H_b = 2 \times 2 = 4\). To determine the splitting pattern of the peak of \(H_b\), use the Pascal’s triangle, based on the observation that, for alkenyl hydrogens, \(J_{trans} > J_{gem}\).
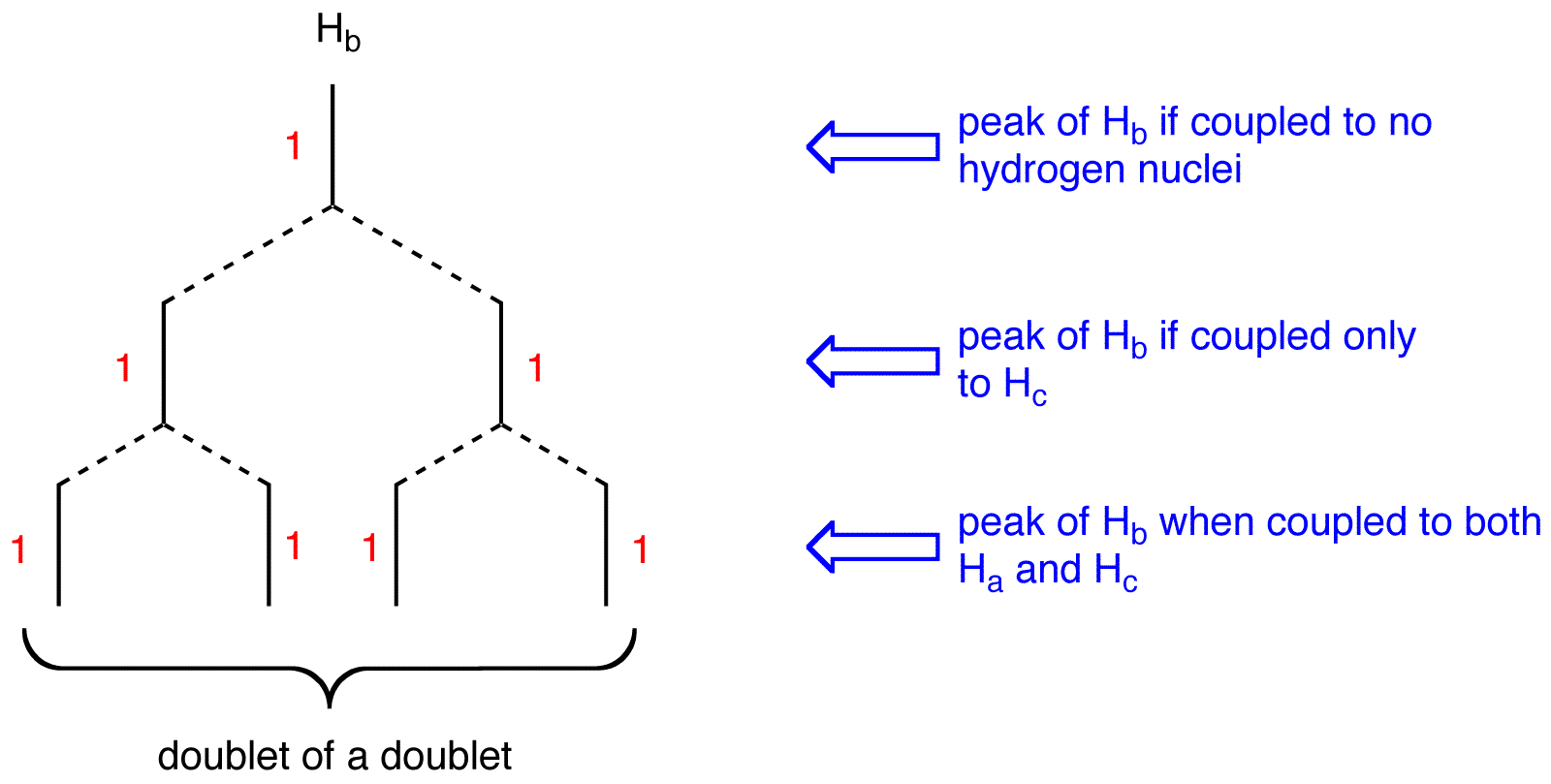
The peak of \(H_b\) is a doublet of a doublet.
peak of \(H_c\):
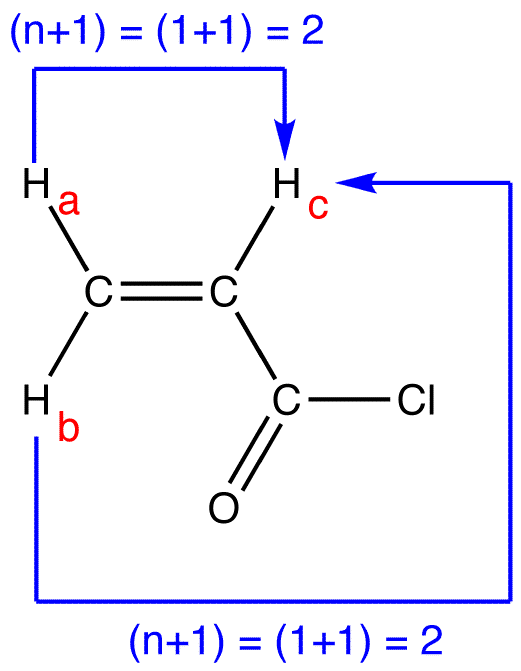
multiplicity of the peak of \(H_c = 2 \times 2 = 4\). To determine the splitting pattern of the peak of \(H_c\), use the Pascal’s triangle based on the observation that, for alkenyl hydrogens, \(J_{trans} > J_{cis}\).
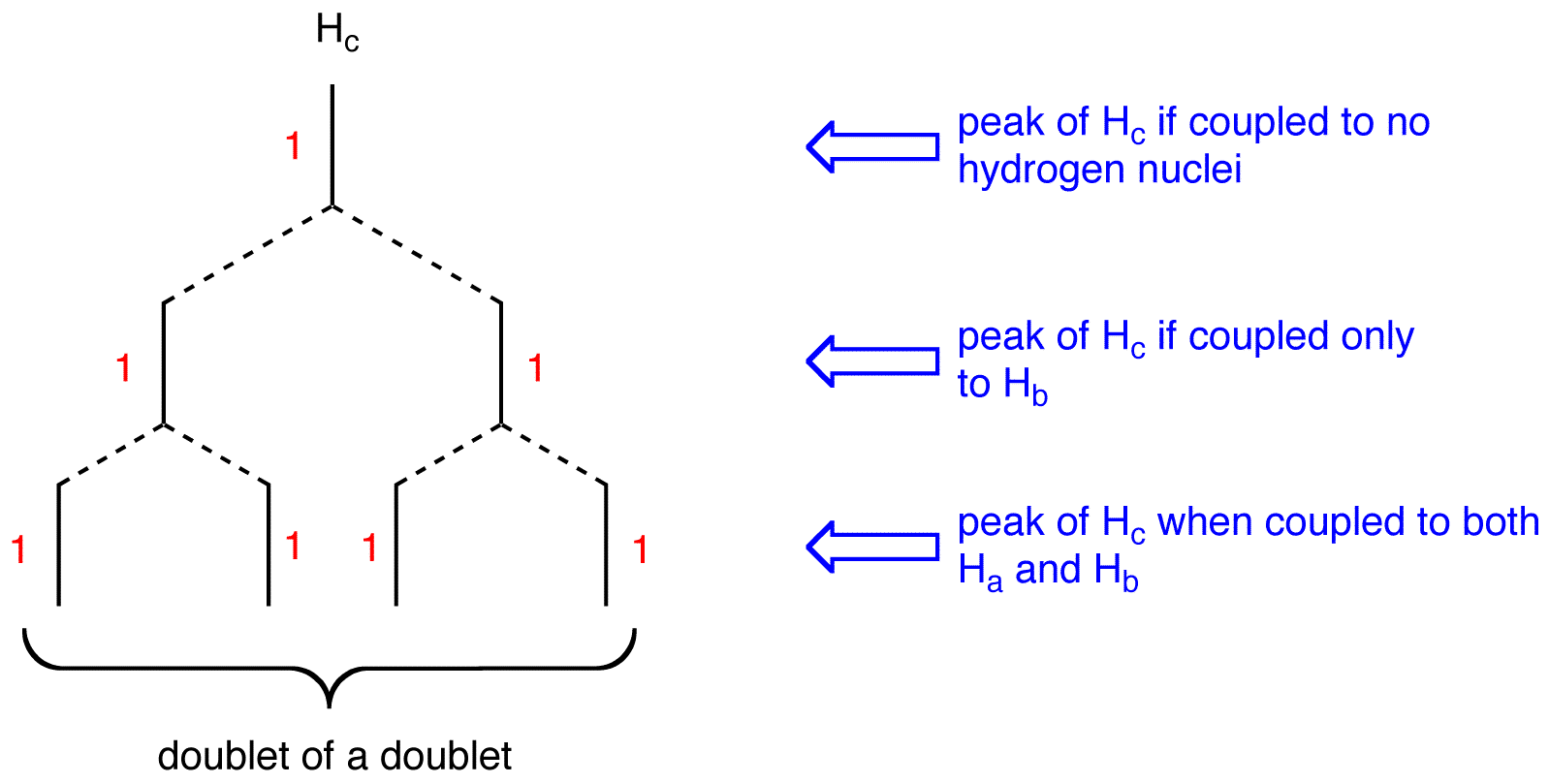
The peak of \(H_c\) is a doublet of a doublet.

