12.13: Symmetry of Vibrations Describes their Spectroscopic Behavior

Vibrational transitions in molecules

The potential energy surface (electronic state), often approximated as a Morse potential, describes the energy of the eigenstate as a function of the interatomic distance. When an electron is excited form one eigenstate to another within the electronic state there is a change in interatomic distance, this result in a vibration occurring.

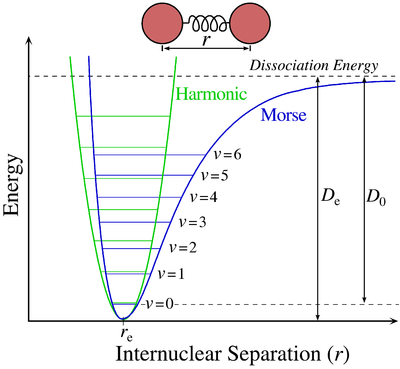
Vibrational transitions oftne occur when a molecule absorbs or emits infrared light, though, as we will see later, there are other processes that can cause vibrational transitions. During the vibrational transition, the electrons remains in the same electronic state, but that vibrational state changes from one eigenstate to another. In the case of the Morse diagram above, the vibrational eigenstates are denoted as \(\nu\). As you can see from the diagram the eigenstate is a function of energy versus interatomic distance. To predict whether a vibrational transition will occur, or for that matter a transition of any kind, we use the transition moment integral:

\[\int \Psi_i*\mu \Psi_f d\tau=\langle \Psi_i | \mu| \Psi_f \rangle\]

The transition moment integral is written here in standard integral format, but this is equivalent to Bra & Ket format which is standard in most chemistry quantum mechanical text (The \(\langle \Psi_i |\) is the Bra portion, \(| \Psi_f \rangle\) is the Ket portion). The transition moment operator \(\mu\) is the operator the couples the initial state \(\Psi_i\) to the final state \(\Psi_f\), which is derived from the time independent Schrödinger equation. However using group theory we can ignore the detailed mathematical methods. We can use the \(\Gamma_{ir}\) of the vibrational energy levels and the symmetry of the transition moment operator to find out if the transition is allowed by selection rules. The selection rules for vibrations or any transition is that is allowed, for it to by allowed by group theory the answer must contain the totally symmetric \(\Gamma_{ir}\), which is always the first \(\Gamma_{ir}\) in the character table for the molecule in question.

Infrared Spectroscopy

Infrared Spectroscopy (IR) measures the vibrations that occur within a single electronic state, such as the one shown above. Because the transition occurs within a single electronic state there is a variation in interatomic distance. The dipole moment is dictate by the equation.

\[ \vec{\mu} = \alpha\vec{E} \]

Where \( \vec{\mu} \) is the magnitude of dipole moment; \( \alpha \) is the polarizability constant (actually a tensor) & \( E \) is the magnitude of the electric field which can be described as the electronegitivity.³ Therefore when a vibration occurs within a single electronic state there is a change in the dipole moment, which is the definition of an active IR transition.

\[ \left ( \frac{\mathrm{d\mu} }{\mathrm{d} q} \right )_{eq} \neq 0 \]

In terms of group theory a change in the dipole is a change from one vibrational state to another, as shown by the equation above. A picture of the vibrational states with respect ot the rotational states and electronic states is given below. In IR spectroscopy the transition occurs only from on vibrational state to another all within the same electronic state, shown below as B.

Light polarized along the \(x\), \(y\), and \(z\) axes of the molecule may be used to excite vibrations with the same symmetry as the \(x\), \(y\) and \(z\) functions listed in the character table.

For example, in the \(C_{2v}\) point group, \(x\)-polarized light (light polarized in the \(x\) direction) may be used to excite vibrations of \(B_1\) symmetry, \(y\)-polarized light to excite vibrations of \(B_2\) symmetry, and \(z\)-polarized light to excite vibrations of \(A_1\) symmetry. In \(H_2O\), we would use \(z\)-polarized light to excite the symmetric stretch and bending modes, and \(x\)-polarized light to excite the asymmetric stretch. Shining \(y\)-polarized light onto a molecule of \(H_2O\) would not excite any vibrational motion.

Where group theory comes in to play is weather or not this transition is allowed by symmetry. This can be determined by the transition moment integral described above. For example if one works through a transition from the ground vibrational state, which is always the totally symmetric in this example A_1g, to a excited vibrational state, B_2u. The possible symmetries for the transition moment operator are A_1g,B_2u,B_2g, for x,y,z transitions repectively (one obtains the transition moment operator from the character table for the ?ir of the x,y,z translations).

<A_1glMlB_2u>, M=A_1g,B_2u or B_2g

From the direct product rules one can work through each of the transiton moment operators and see if the awnser contains the totally symmetric ?ir. The first direct product gives a A_1gxA_1gxB_2u=B_2u, so this transition is not x polarized. The y polarized transition moment operator gives A_1gxB_2uxB_2u=A_1g, this transition is allowed by symmetry. The final polarization z, gives A_1gxB_2gxB_2u=A_1u, this transition is also not allowed by symmetry. So this IR transition is allowed by y polarized light in this molecule.

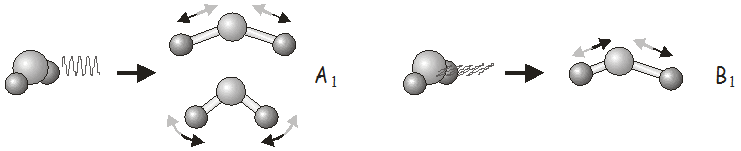
Raman Scattering

If there are vibrational modes in the molecule that may not be accessed using a single photon, it may still be possible to excite them using a two-photon process known as Raman scattering. An energy level diagram for Raman scattering is shown below.

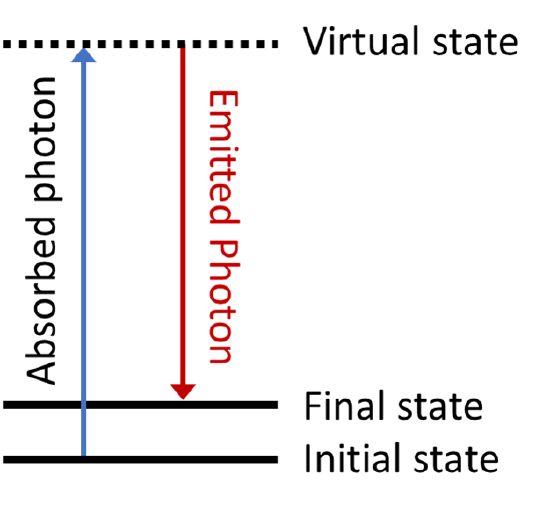
The first photon excites the molecule to some high-lying intermediate state, known as a virtual state. Virtual states are not true stationary states of the molecule (i.e. they are not eigenfunctions of the molecular Hamiltonian), but they can be thought of as stationary states of the ‘photon + molecule’ system. These types of states are extremely short lived, and will quickly emit a photon to return the system to a stable molecular state, which may be different from the original state. Since there are two photons (one absorbed and one emitted) involved in Raman scattering, which may have different polarizations, the transition dipole for a Raman transition transforms as one of the Cartesian products \(x^2\), \(y^2\), \(z^2\), \(xy\), \(xz\), \(yz\) listed in the character tables.

Vibrational modes that transform as one of the Cartesian products may be excited by a Raman transition, in much the same way as modes that transform as \(x\), \(y\), or \(z\) may be excited by a one-photon vibrational transition.

In \(H_2O\), all of the vibrational modes are accessible by ordinary one-photon vibrational transitions. However, they may also be accessed by Raman transitions. The Cartesian products transform as follows in the \(C_{2v}\) point group.

\[\begin{array}{clcl} A_1 & x^2, y^2, z^2 & B_1 & xz \\ A_2 & sy & B_2 & yz \end{array} \tag{27.5}\]

The symmetric stretch and the bending vibration of water, both of \(A_1\) symmetry, may therefore be excited by any Raman scattering process involving two photons of the same polarization (\(x\)-, \(y\)- or \(z\)-polarized). The asymmetric stretch, which has \(B_1\) symmetry, may be excited in a Raman process in which one photon is \(x\)-polarized and the other \(z\)-polarized.