7.1: Thermodynamics of Mixing
- Page ID
- 84330
A natural place to begin a discussion of mixtures is to consider a mixture of two gases. Consider samples of the two gases filling two partitions in a single container, both at the same pressure, temperature, having volumes \(V_A\) and \(V_B\).

After being allowed to mix isothermally, the partial pressures of the two gases will drop by a factor of 2 (although the total pressure will still be the original value) and the volumes occupied by the two gases will double.

Enthalpy of Mixing
Assuming ideal behavior, so that interactions between individual gas molecules are unimportant, it is fairly easy to calculate \(Delta H) for each gas, as it is simply an isothermal expansion. The total enthalpy of mixing is then given by
\[\Delta H_{mix} = \Delta H_A + \Delta H_B \nonumber \]
And since the enthalpy change for an isothermal expansion of an ideal gas is zero,
\[\Delta H_{mix} =0 \nonumber \]
is a straight-forward conclusion. This will be the criterion for an ideal mixture.
In general, real mixtures will deviate from this limiting ideal behavior due to interactions between molecules and other concerns. Also, many substances undergo chemical changes when they mix with other substances. But for now, we will limit ourselves to discussing mixtures in which no chemical reactions take place.
Entropy of Mixing
The entropy change induced due to isothermal mixing (assuming again no interactions between the molecules in the gas mixture) is again going to be the sum of the contributions from isothermal expansions of the two gases. Fortunately, entropy changes for isothermal expansions are easy to calculate for ideal gases.
\[\Delta S = nR \ln \left( \dfrac{V_2}{V_1}\right) \nonumber \]
If we use the initial volumes VA and VB for the initial volumes of gases A and B, the total volume after mixing is \(V_A + V_B\), and the total entropy change is
\[\Delta S_{mix} = n_AR \ln \left( \dfrac{V_A + V_B}{V_A}\right) + n_AR \ln \left( \dfrac{V_A + V_B}{V_B}\right) \nonumber \]
Noting that the term
\[ \dfrac{V_A + V_B}{V_A} = \dfrac{1}{\chi_A} \nonumber \]
where \(\chi_A\) is the mole fraction of \(A\) after mixing, and that \(n_A\) can be expresses as the product of \(\chi_A\) and the total number of moles, the expression can be rewritten
\[\Delta S_{mix} = n_{tot} R \left[ -\chi_A \ln (\chi_A) - \chi_B \ln (\chi_B) \right] \nonumber \]
It should be noted that because the mole fraction is always between 0 and 1, that \(\ln (\chi_B) < 0\). As such, the entropy change for a system undergoing isothermal mixing is always positive, as one might expect (since mixing will make the system less ordered).
The entropy change for a system undergoing isothermal mixing is always positive.
Free Energy of Mixing
Calculating \(\Delta G_{mix}\) should be no more difficult than calculating \(\Delta S_{mix}\). For isothermal mixing and constant total pressure
\[ \Delta G_{mix} = \Delta H_{mix} - T\Delta S_{mix} \nonumber \]
and so it follows from above that for the isothermal mixing of two gases at constant total pressure
\[\Delta G_{mix} = n_{tot} RT \left[ -\chi_A \ln (\chi_A) + \chi_B \ln (\chi_B) \right] \nonumber \]
The relationships describing the isothermal mixing of two ideal gases \(A\) and \(B\) is summarized in the graph below.
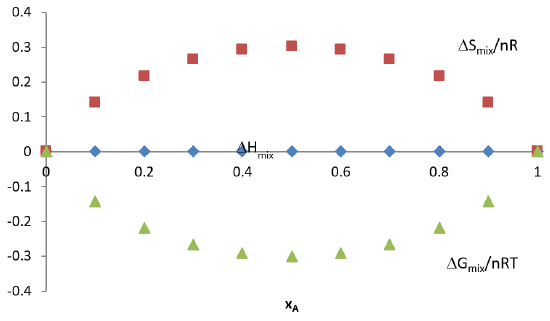
Again, because \(\ln (\chi_i) < 0\), then \(\Delta G_{mix} < 0\) implying that mixing is always a spontaneous process for an ideal solution. This is true for gases. But for many combinations of liquids or solids, the strong intermolecular forces may make mixing unfavorable (for example in the case of vegetable oil and water). Also, these interactions may make the volume non-additive as well (as in the case of ethanol and water).
Mixing is always a spontaneous process for an ideal solution.


