10.1: General Principles of Catalysis
- Page ID
- 41361
As can be seen from the Arrhenius equation, the magnitude of the activation energy, \(E_a\), determines the value of the rate constant, \(k\), at a given temperature and thus the overall reaction rate. Catalysts provide a means of reducing \(E_a\) and increasing the reaction rate. Catalysts are defined as substances that participate in a chemical reaction but are not changed or consumed. Instead they provide a new mechanism for a reaction to occur which has a lower activation energy than that of the reaction without the catalyst. Homogeneous catalysis refers to reactions in which the catalyst is in solution with at least one of the reactants whereas heterogeneous catalysis refers to reactions in which the catalyst is present in a different phase, usually as a solid, than the reactants. Figure \(\PageIndex{1}\) shows a comparison of energy profiles of a reaction in the absence and presence of a catalyst.
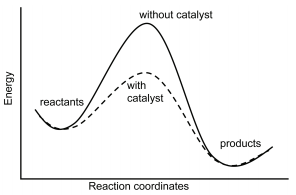
Consider a non-catalyzed elementary reaction
\[\text{A} \overset{k}{\longrightarrow} \text{P}\]
which proceeds at rate \(k\) at a certain temperature. The reaction rate can be expressed as
\[\dfrac{d \left[ \text{A} \right]}{dt} = -k \left[ \text{A} \right] \label{Eq1}\]
In the presence of a catalyst \(\text{C}\), we can write the reaction as
\[\text{A} + \text{C} \overset{k_\text{cat}}{\longrightarrow} \text{P} + \text{C}\]
and the reaction rate as
\[\dfrac{d \left[ \text{A} \right]}{dt} = -k \left[ \text{A} \right] - k_\text{cat} \left[ \text{A} \right] \left[ \text{C} \right] \label{Eq2}\]
where the first term represents the uncatalyzed reaction and the second term represents the catalyzed reaction. Because the reaction rate of the catalyzed reaction is often magnitudes larger than that of the uncatalyzed reaction (i.e. \(k_\text{cat} \gg k\)), the first term can often be ignored.
Acid Catalysis
A common example of homogeneous catalysts are acids and bases. For example, given an overall reaction is \(\text{S} \rightarrow \text{P}\). If \(k\) is the rate, then
\[\dfrac{d \left[ \text{P} \right]}{dt} = k \left[ \text{S} \right]\]
The purpose of an enzyme is to enhance the rate of production of the product \(\text{P}\). The equations of the acid-catalyzed reaction are
\[\begin{align} \text{S} + \text{A}H &\overset{k_1}{\underset{k_{-1}}{\rightleftharpoons}} \text{S}H^+ + \text{A}^- \\ \text{S}H^+ + H_2 O &\overset{k_2}{\rightarrow} \text{P} + H_3 O^+ \\ H_3 O^+ + \text{A}^- &\overset{k_3}{\underset{k_{-3}}{\rightleftharpoons}} \text{A}H + H_2 O \end{align}\]
The full set of kinetic equations is
\[\begin{align} \dfrac{d \left[ \text{S} \right]}{dt} &= -k_1 \left[ \text{S} \right] \left[ \text{A} H \right] + k_{-1} \left[ \text{S} H^+ \right] \left[ \text{A}^- \right] \\ \dfrac{ d \left[ \text{A} H \right]}{dt} &= -k_1 \left[ \text{S} \right] \left[ \text{A} H \right] + k_{-1} \left[ \text{S} H^+ \right] \left[ \text{A}^- \right] - k_{-3} \left[ \text{A} H \right] + k_3 \left[ H_3 O^+ \right] \left[ \text{A}^- \right] \\ \dfrac{d \left[ \text{S} H^+ \right]}{dt} &= k_1 \left[ \text{S} \right] \left[ \text{A} H \right] - k_{-1} \left[ \text{S} H^+ \right] \left[ \text{A}^- \right] - k_2 \left[ \text{S} H^+ \right] \\ \dfrac{d \left[ \text{A}^- \right]}{dt} &= k_1 \left[ \text{S} \right] \left[ \text{A} H \right] - k_{-1} \left[ \text{S} H^+ \right] \left[ \text{A}^- \right] -k_2 \left[ \text{A}^- \right] \left[ H_3 O^+ \right] + k_{-3} \left[ \text{A} H \right] \\ \dfrac{d \left[ \text{P} \right]}{dt} &= k_2 \left[ \text{S} H^+ \right] \\ \dfrac{d \left[ H_3 O^+ \right]}{dt} &= -k_2 \left[ \text{S} H^+ \right] - k_3 \left[ H_3 O^+ \right] \left[ \text{A}^- \right] + k_{-3} \left[ \text{A} H \right] \end{align} \label{Eq3}\]
We cannot easily solve these, as they are nonlinear. However, let us consider two cases \(k_2 \gg k_{-1} \left[ \text{A}^- \right]\) and \(k_2 \ll k_{-1} \left[ \text{A}^- \right]\). In both cases, \(\text{S} H^+\) is consumed quickly, and we can apply a steady-state approximation:
\[\dfrac{d \left[ \text{S} H^+ \right]}{dt} = k_1 \left[ \text{S} \right] \left[ \text{A} H \right] - k_{-1} \left[ \text{A}^- \right] \left[ \text{S} H^+ \right] - k_2 \left[ \text{S} H^+ \right] = 0 \label{Eq4}\]
Rearranging in terms of \(\text{S} H^+\) yields
\[\left[ \text{S} H^+ \right] = \dfrac{k_1 \left[ \text{S} \right] \left[ \text{A} H \right]}{k_{-1} \left[ \text{A}^- \right] + k_2} \label{5}\]
and the rate of production of \(\text{P}\) can be written as
\[\dfrac{d \left[ \text{P} \right]}{dt} = k_2 \left[ \text{S} H^+ \right] = \dfrac{k_1 k_2 \left[ \text{S} \right] \left[ \text{A} H \right]}{k_{-1} \left[ \text{A}^- \right] + k_2} \label{Eq6}\]
In the case where \(k_2 \gg k_{-1} \left[ \text{A}^- \right]\), Equation \(\ref{Eq6}\) can be written as
\[\dfrac{d \left[ \text{P} \right]}{dt} = k_1 \left[ \text{S} \right] \left[ \text{A} H \right] \label{Eq7}\]
which is known as a general acid-catalyzed reaction. On the other hand, if \(k_2 \ll k_{-1} \left[ \text{A}^- \right]\), we can use an equilibrium approximation to write the rate of production of \(\text{P}\) as
\[\dfrac{d \left[ \text{P} \right]}{dt} = \dfrac{k_1 k_2 \left[ \text{S} \right] \left[ \text{A} H \right]}{k_{-1} \left[ \text{A}^- \right]} = \dfrac{k_1 k_2}{k_{-1} K} \left[ \text{S} \right] \left[ H^+ \right] \label{Eq8}\]
where \(K\) is the acid dissociation constant:
\[K = \dfrac{ \left[ \text{A}^- \right] \left[ H^+ \right]}{\left[ \text{A} H \right]} \label{Eq9}\]
In this case, the reaction is hydrogen ion-catalyzed.
Enzyme Catalysis
To live, grow, and reproduce, microorganisms undergo a variety of chemical changes. They alter nutrients so they can enter the cell and they change them once they enter in order to synthesize cell parts and obtain energy.
Metabolism refers to all of the organized chemical reactions in a cell. Reactions in which chemical compounds are broken down are called catabolic reactions while reactions in which chemical compounds are synthesized are termed anabolic reactions. All of these reactions are under the control of enzymes.
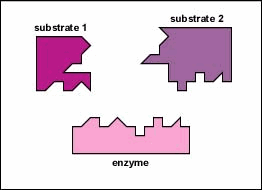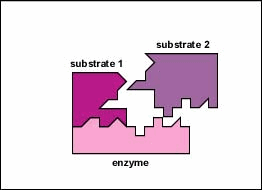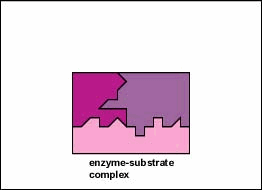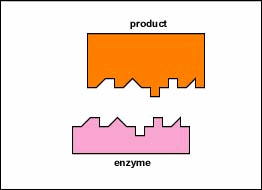
Enzymes are substances present in the cell in small amounts that function to speed up or catalyze chemical reactions. On the surface of the enzyme is usually a small crevice that functions as an active site or catalytic site to which one or two specific substrates are able to bind. (Anything that an enzyme normally combines with is called a substrate.) The binding of the substrate to the enzyme causes the flexible enzyme to change its shape slightly through a process called induced fit to form a tempore intermediate called an enzyme-substrate complex (Figure 1).
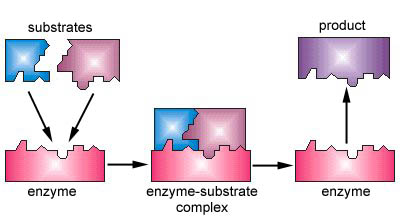
Enzymes speed up the rate of chemical reactions because they lower the energy of activation, the energy that must be supplied in order for molecules to react with one another (Figure \(\PageIndex{3}\)). Like homogeneous catalysts discussed above, enzymes lower the energy of activation by forming an enzyme-substrate complex allowing products of the enzyme reaction to be formed and released (Figure \(\PageIndex{2}\)).
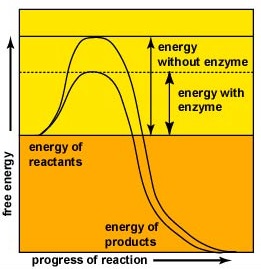
Enzyme-Substrate Reactions
Enzymes are substances present in the cell in small amounts which speed up or catalyze chemical reactions. Enzymes speed up the rate of chemical reactions because they lower the energy of activation, the energy that must be supplied in order for molecules to react with one another. Enzymes lower the energy of activation by forming an enzyme-substrate complex.
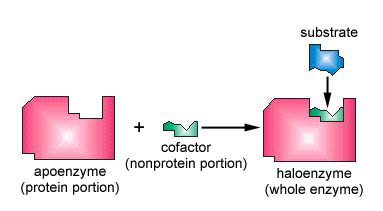
Many enzymes require a nonprotein cofactor to assist them in their reaction. In this case, the protein portion of the enzyme, called an apoenzyme, combines with the cofactor to form the whole enzyme or haloenzyme (Figure \(\PageIndex{4}\)). Some cofactors are ions such as Ca++, Mg++, and K+; other cofactors are organic molecules called coenzymes which serve as carriers for chemical groups or electrons. NAD+, NADP+, FAD, and coenzyme A (CoA) are examples of coenzymes.
Enzymes are generally globular proteins. (Some RNA molecules called ribozymes can also be enzymes. These are usually found in the nuclear region of cells and catalyze the splitting of RNA molecules.). Enzymes are catalysts that breakdown or synthesize more complex chemical compounds. They allow chemical reactions to occur fast enough to support life. Enzymes speed up the rate of chemical reactions because they lower the energy of activation, the energy that must be supplied in order for molecules to react with one another. Anything that an enzyme normally combines with is called a substrate. Enzymes are very efficient with a typically enzyme generally able to catalyze between 1 and 10,000 molecules of substrate per second. The means that enzymes are only have to be present in small amounts in the cell since. They are not altered during their reaction and are highly specific for their substrate, with generally one specific enzyme dedicated for each specific chemical reaction.
Factors that affect the rate of enzyme reactions
Enzyme activity is affected by a number of factors including:
- The concentration of enzyme: Assuming a sufficient concentration of substrate is available, increasing enzyme concentration will increase the enzyme reaction rate.
- The concentration of substrate: At a constant enzyme concentration and at lower concentrations of substrates, the substrate concentration is the limiting factor. As the substrate concentration increases, the enzyme reaction rate increases. However, at very high substrate concentrations, the enzymes become saturated with substrate and a higher concentration of substrate does not increase the reaction rate.
- Inhibitors: inhibitors will inhibit the activity of enzyme and decrease the rate of reaction. Enzyme inhibitors will bind to enzyme active sites and could modify the chemistry of an active site which can stop a substrate from entering.
- The temperature: Each enzyme has an optimum temperature at which it works best. A higher temperature generally results in an increase in enzyme activity (Arrhenius kinetics). As the temperature increases, molecular motion increases resulting in more molecular collisions. If, however, the temperature rises above a certain point, the heat will denature the enzyme, causing it to lose its three-dimensional functional shape by denaturing its hydrogen bonds. Cold temperature, on the other hand, slows down enzyme activity by decreasing molecular motion.
- The pH: Each enzyme has an optimal pH that helps maintain its three-dimensional shape. Changes in pH may denature enzymes by altering the enzyme's charge. This alters the ionic bonds of the enzyme that contribute to its functional shape.
- The salt concentration: Each enzyme has an optimal salt concentration. Changes in the salt concentration may also denature enzymes.
Applications of Enzymes
Enzymes are essential to maintain homeostasis because any malfunction of an enzyme could lead to diseases. Therefore, pharmaceutical companies study enzyme to manipulate and synthesis new medicine. Besides their medicinal applications, enzymes in industry are important because enzymes help breaking down cellulose, wastes, etc. Enzymes are essential in the process of making new products in many industries such as pharmaceutical, food, paper, wine, etc.
References
- "Chapter 4 Enzyme."Copyrighted IHW, Oct. 2005. Web. 5 Mar. 2011. biologymad.com/resources/Ch%2...0-20enzyme.pdf
- Chang, Raymond. Physical Chemistry for the Biosciences. Sausalito, CA: University Science Books, 2005. Pages 363-384.
Contributors and Attributions
Dr. Gary Kaiser (COMMUNITY COLLEGE OF BALTIMORE COUNTY, CATONSVILLE CAMPUS)

