9.E: Chemical Kinetics (Exercises)
- Page ID
- 41334
9.1: Reaction Rates
Q9.1
Write the rate of reaction in terms of the rate of disappearance of reactant and the rate of formation of products:
- \(NO_{(g)} + O_{3 (g)} \rightarrow NO_{2(g)} + O_{2(g)}\)
- \(2C_2H_{6 (g)} + 7O_{2(g)} \rightarrow 4 CO_{2(g)} + 6 H_2O_{(aq)}\)
- \(H_{2 (g)} + I_{2 (g)} \rightarrow 2HI_{(g)} \)
- \(4OH_{(g)} + H_2S_{(g)} \rightarrow SO_{2(g)} + 2H_2O_{(aq)} + H_{2(g)}\)
S9.1
- \(\text{rate of reaction} = \dfrac{-∆[NO]}{∆t} = \dfrac{-∆[O_3]}{∆t} = \dfrac{∆[NO_2]}{∆t} = \dfrac{∆[O_2]}{∆t} \)
- \(\text{rate of reaction} = \dfrac{-∆[C_2H_6]}{2∆t} = \dfrac{-∆[O_2]}{ 7∆t} =\dfrac{∆[CO_2]}{4∆t} = \dfrac{∆[H_2O]}{6∆t} \)
- \(\text{rate of reaction} = \dfrac{-∆[H_2]}{ ∆t} = \dfrac{-∆[I_2]}{∆t} = \dfrac{∆[HI]}{2∆t} \)
- \(\text{rate of reaction} = \dfrac{-∆[OH]}{4∆t} = \dfrac{-∆[H_2S]}{∆t} = \dfrac{∆[SO_2]}{∆t} = \dfrac{∆[H_2O]}{∆t} = \dfrac{∆[H_2]}{∆t} \)
9.2: Reaction Order
Q9.2
Determine the value of the rate constant for the elementary reaction:
\[I_{2(g)} + H_{2 (g)} \rightarrow 2HI_{(aq)}\]
given that when [Br2] is 0.15 M and [H2] is 0.2M, the rate of reaction is 0.005 M s-1 at 298 K.
S9.2
rate of reaction = k[Br2][H2]
0.005 Ms-1 =k ( 0.15M)2(0.2M)
k= 1.11 M-1s-1
Q9.3
Given the rate of the third order reaction:
\[A + B + C \rightarrow P \]
is 0.05 Ms-1
If the [A] = 0.05 M, [B] = 0.01M, and [C] = 0.25M. What is the third order rate constant?
S9.3
rate of reaction = k[A][B][C]
0.05Ms-1 =k (0.05M)(0,01M)(0.25M)
k= 0.05Ms-1/( 0.05) (0.01)( 0.25) M3
k= 400M-2s-1
Q9.3
What are the units of the rate constant for a second-order reaction?
S9.3
The reaction rate:Q9.4
Calculate the fraction of the starting quantity of A that will be used up after 60 s. Given the reaction below which is found to be the first order in A and \(t_{1/2} = 40\;s\)
\[ A \rightarrow B + C\]
S9.4
with \(t_{1/2} = 40 \; s\]
The remain of fraction A after 60 s:
The fraction will be used up after 60s:
Q9.5
Given the first order reaction is completed 90% in 30 mins at 298 K. Calculate the rate constant.
Q9.6
Assume the half life of the first order decay of radioactive isotope takes about 1 year (365 days). How long will it take the radioactivity of that isotope to decay by 60%?
Q9.7a
The decomposition of dinitrogen peroxide (\(N_2O_5\)) is a first-order reaction with a rate constant of 0.045 min-1 at 300 K.
\[2 N_{2}O_{5(g)} \rightarrow 4NO_{2}(g)+O_{2}\]
If there were initially 0.040 mol of \(N_2O_5\), calculate the moles of \(N_2O_5\) remaining after 5 minutes.S9.7a
The integrated rate equation of a first-order reaction is:
\[[A] = [A]_{0}e^{-kt}\]
Substituting concentration for moles of reactant and plugging in the known values:
\[n_{A} = 0.040_{0}e^{-0.045*5}\]
\[n_{A} = 0.032\]
Q9.7b
S9.7b
First, you need to figure the half life of your compound. We do this by solving for k:
\[t_{1/2}=\dfrac{0.693}{k}\]
\[k=\dfrac{0.693}{t\dfrac{1}{2}}\]
\[k=\dfrac{0.693}{2 hrs} =0.3465\]
with this half life, we can find the time it will take by solving for t:
\[ln\dfrac{[A]}{[A]^{_{o}}}=-kt\]
We do not have the initial and final concentration, but that is okay.
Assuming the initial concentration is 100 g, we can assume that the final concentration is 10 g because that would be reduced 90% as stated in the problem.
\[ln\dfrac{[10]}{[100]}=-kt\]
\[\dfrac{ln[0.1]}{-0.3465}=t=6.65\; hours\]
So 5 hours will be definitely not enough time to reduce the compound
Q9.8a
S9.8a
\[t_{1/2}=\dfrac{0.693}{k}\]
\[t_{1/2}=\dfrac{0.693}{1.5x10^{^{-4}}}\]
\[=4.62 \times 10^3\; mins\]
Q9.8b
The half-life of a second order reaction \[2A\rightarrow P\] is given by:
\[t_{1/2}=\dfrac{1}{k[A]_{o}}\]
Calculate the half-life of a reaction with initial reactant concentration [A] = 0.90 M and a rate constant of 0.20 M-1 min-1.S9.8b
\[t_{1/2} = \dfrac{1}{0.20\times 0.90} = 0.18 min^{-1}\]Q9.9a
S9.9a
A reaction whose half-life changes when the reactant concentration is changed is a second-order reaction. \[t_{1/2} = \dfrac{1}{k[A]_{o}}\] \[k = \dfrac{1}{[A]_{0}t_{1/2}}\] \[k = \dfrac{1}{(0.4M)(5min)} = 0.5 M^{-1}min^{-1}\]Q9.9b
S9.9b
Q9.10a
Calculate the order of the reaction and the rate constant of Cytobutane decompose to ethylene based on equation
\[C_4H_{8 g)} \rightarrow 2C_2H_{4(g)}\]
and temperature at 2150C, constant volume, the pressure 200, 158, 124, 98, 77.5, 61 mmHg.Q9.10b
Given the following data of concentration [A] over a period of time, decide if the data represents first order or second order. Solve for K. Show graphs.

S9.10b
The data best fits a Second order graph.
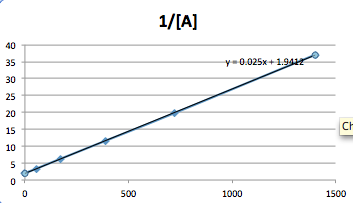
The equation for a second order reaction is:
1/[A]= kt+ 1/[A0]
When solving for K, the equation is rearranged to:
1/[A]- 1/[A0] =k
t
Plug in the numbers given:
1/[.3]- 1/[.5]= k
(0-54)
.025=k
One, can also obtain the slop of the graph and k=.025
Q9.11a
If a compound’s ½ life is 15.6 days. What is the value of k? How long will it take to decompose to 10%. Use first order reaction.
S9.11a
Equation for half-life of a First-Order Reaction is:
\[ t_½ = \dfrac{\ln (2)}{k}\]
If we plug in the information given:
\[15.6 days= \dfrac{\ln(2)}{k}\]
\[k=4.4 \times 10^{-2}\, day^{-1}\]
The second equation needed is the first order reaction, which is:
ln([A]/[A0])= -kt1/2
so, ln ([A]/[A0])=.1
t=-1/k x ln([A]/[A0])
t= -1/(4.4 x 10-2 day-1) x (.1)
t=52 days
12) In a second order reaction 2A--> products, the final concentration is .28M. What is the initial concentration if k=.32M-1s-1 and the times is 5 seconds.
Solution:
Second order reaction equation is:
1/[A]= kt+ 1/[A0]
Filling the information given:
1/[.28M]=.32M-1s-1(5)+ 1/[A0]
1/[A0]= 1.97
[A0]= .50M
Q9.11b
Calculate the half life of a compound if 90% of a given sample of the compound decomposed in 30minS9.11b
[A]=[A]0 e^-kt
[A]0 = 90%
[A] = 10%
t = 30min * 60s/1min = 1800s
[10%]/[90%]=e^ -k*1800
ln[10%/90%]/1800 = k = 3.95E-4
t1/2= ln(2)/k
t1/2 = .693/3.95E-4= 1754s
1754s*1min/60s = 29 min
Q9.12
Given rate constant for second order reaction
\[2 NO_{2(g)} \rightarrow 2NO_{(g)} + O_{2(g)}\]
is 1.08 M-1s-1 at 600 0 C. Find the time that would take for the concentration of NO2 from 1.24 M to 0.56 M?
S9.12
1/ [A] – 1/[A]0 = kt
t= 1/k ( 1/[A] – 1/[A]0)
= (1/ 1.08 M-1s-1 ) (1/0.56 – 1/1.24) = 7.2 s
Q9.13a
Is which order of reaction half-life is independent of initial concentration?
S9.13a
First order because the half-life equation for first order is
t1/2= ln(2)/k, it does not have [A0]
Q9.13b
The decomposition of N2) is the first order. At 3650C, t1/2 is 1.79 x 103 min. given intial pressure of 1.05 atm.. Calculate total pressure.
S9.13b
\[\begin{align} P &= P_{N_2O} + P_{N_2} + P_{O_2} \\ &= 0.525 + 0.525 +0.2625 = 1.31 \;atm \end{align}\]
Q9.14a
The integrated rate law for the zero-order reaction A → B is [A]t = [A]0 - kt
a) skektch the following plots:
(i) rate vs. [A]
(ii) [A] vs. t
S9.14a
rate = k
rate is independent of [A]
(ii) [A] vs. t
[A]t = [A]0 - kt
b) Derive an expression for the half-life of the reaction.
At t = t1/2 , [A] = [A]0/2 so, [A]0/2 = [A]0 - kt1/2
t1/2 = 1/2k [A}0
c) Calculate the time in half-lives when the integrated rate law is no longer valid (that is, when [A] = 0)
[A]t = 0 = [A]0 - kt
t1/2 = 1/2k [A}0 ⇒ k = 1/2t1/2 [A}0
Therefore, to consume all of the reactants it takes
t = [A}0/k = [A]0/2 so, [A]0 / (1/(2t1/2)) [A]0 = 2t1/2
integrated rate law is no longer valid after 2 half-lives
Q9.14b
Jack, Jill, and you are in a physical chemistry class. The professor writes the following equations on the black board.
\[A\rightarrow B\]
\[[A]=[A_{0}]e^{-kt}\]
- The professor assigns you to derive the first-order reaction in front of the class.
- Jack was assigned to find the rate constant if the reaction half-life is 10 hours. Since you are a good friend of Jack, you decide to help him double check his answer by solving for the rate constant.
S9.14b
a)
\[\int ^{[A]}_{[A]_{0}} \dfrac{d[A]}{[A]}=\int^{t}_{0} -kdt\]
\[\ln[A] \mid ^{[A]}_{[A]_{0}} = -kt\]
\[\ln[A] -\ln[A]_{0}=-kt\]
\[\ln\dfrac{[A]}{[A]_{0}} =-kt\]
\[\dfrac{[A]}{[A]_{0}}=e^{-kt}\]
\[[A]=[A_{0}]e^{-kt}\]
b)
\[t_{1/2}=\dfrac{\ln 2}{k}\]
\[10 hours = \dfrac{\ln2}{k}\]
\[k=\dfrac{\ln2}{10 hours}\times\dfrac{1hour}{60min}\times\dfrac{1min}{60secs}\]
\[k=\]
Q9.15a
In the nuclear industry, workers use a rule of thumb that the readioactivity from any sample will be relatively harmless after 10 half-lives. Calculate the fraction of a radioactive sample that remains after this time period (hint: Radioactive decay obeys first-order kinetics)
S9.15a
[A] = [A]oe-kt
t1/2 = ln2 / k
[A] = (100)e-(1)(10) =.00454
% remaining after 10 half-lives
Q9.15b
- Radioactive decay occurs in what order?
- The gas used in the simulation is harmless because the fraction of the original remaining is 0.004 and the time that passed 30 years. What is the rate constant?
S9.15b
a) Radioactive decay occurs in first order.
b)
\[\dfrac{[A]}{[A]_{0}}=e^{-kt}\]
\[0.004=e^{-k\,30years}\]
\[\ln[0.004]=-k\,30years\]
\[k=\dfrac{-30}{\ln[0.004]}\]
Q9.16a
Many reactions involving heterogeneous catalysis are zero order; that is, rate = k. An example is the decomposition of phosphine (\(\ce{PH3}\)) over tungsten (W):
\[\ce{4PH3(g) →P4(g) + 6H2(g)}\]
The rate for this reaction is independent of [PH3] as long as phosphine's pressure is sufficiently high (>= 1 atm). Explain.
S9.16a
With sufficient PH3, all of the catalytic sites on the tungsten surface are occupied. Further increases in the amount of phosphine cannot affect the reaction, and the rate is independent of [PH3].
Q9.16b
Jill and you just went to an enzyme kinetic workshop. However, Jill is confused about why at high concentrations of substrates the reaction order is zero-order. Please explain to Jill in a way that anyone can understand.S9.16b
9.3: Molecularity of a Reaction
Q9.41a
A mixture of compounds M and N whose half-lives are 40 minutes and 17 minutes, respectively. They decompose by first-order kinetics. If their concentrations are equal initially, how long does concentration of N to be half that of M?
S9.41a
[I] is the initial concentration of M and N
-> t = 30.1 min
Q9.41b
Compounds A and B both decay by first-order kinetics. The half-life of A is 20 minutes and the half-life of B is 48 minutes. If a container initially contains equal concentrations of compounds A and B, after how long will the concentration of B be twice that of A?
S9.41b
1. Write, in mathematical terms, the information given in the problem and what the problem is asking for.
\[ t_{1/2, A} = 20.0 min \]
\[ t_{1/2, B} = 48.0 min \]
\[ [A]_0 = [B]_0 \]
A and B decay by first-order, so
\[ -\dfrac{d[A]}{dt} = k_A [A] \]
\[ -\dfrac{d[B]}{dt} = k_B [B] \]
(Note: the rate constants for A and B are not equal, so indicate which is which with subscripts.)
Want find t at which the following is true:
\[ [B] = 2[A] \]
2. Substitute the integrated rate equations for [A] and [B]
\[ [B]_0 e^{-k_B t} = 2 [A]_0 e^{-k_A t} \]
3. Write expressions for the rate constants in terms of half-lives, and substitute into the equation.
\[ t_{1/2, A} = \dfrac{ln2}{k_A} \Rightarrow k_A = \dfrac{ln2}{t_{1/2, A}} \]
\[ t_{1/2, B} = \dfrac{ln2}{k_B} \Rightarrow k_B = \dfrac{ln2}{t_{1/2, B}} \]
\[ [B]_0 e^{-\dfrac{ln2}{t_{1/2, B}} t} = 2 [A]_0 e^{-\dfrac{ln2}{t_{1/2, B}} t} \]
4. Solve for t
Since initial concentrations of A and B are equal:
\[ e^{-\dfrac{ln2}{t_{1/2, B}} t} = 2 e^{-\dfrac{ln2}{t_{1/2, B}} t} \]
Take natural log of both sides:
\[ -\dfrac{t}{t_{1/2, B}} ln2 = \left ( 1 - \dfrac{t}{t_{1/2, A}} \right ) ln2 \]
\[ t = \dfrac{1}{\dfrac{1}{t_{1/2, A}} - \dfrac{1}{t_{1/2, B}}} \]
5. Plug in values for half-lives
\[ t = \dfrac{1}{\dfrac{1}{20.0 min} - \dfrac{1}{48.0 min}} = 34.2\ min \]
Answer: 34.2 minutes
Q9.42a
In Q3 thermodynamics and in Q9 chemical kinetics, the term “reversible “ is used. How do you understand this term? (it has a same meaning in these two chapters)
S9.42a
Actually, this word is used to describe a “reversible” reaction in which both forward and backward reactions can happen in kinetics. In thermodynamics, “reversible” is used to describe a process that is in equilibrium along the pathway from the initial to final states.
Q9.42b
If a reaction has come to thermodynamic equilibrium, can we say anything in particular about the system's kinetics?
S9.42b
Equilibrium occurs when all reactants and products are being consumed at the same rate that they are created. Take the simple example:
\[ A\underset{k_{-1}}{\overset{k_1}{\rightleftharpoons}}B \]
When the system is at equilibrium,
\[ \dfrac{d[A]}{dt} = \dfrac{d[B]}{dt} = 0 \]
\[ k_{-1} [A] = k_1 [B] \]
\[ \dfrac{k_{-1}}{k_1} = \dfrac{[B]}{[A]} \]
\[ K_{eq} = \dfrac{k_{-1}}{k_1} \]
Q9.43a
The recombination of bromine atoms in an organic solvent, like carbon tetrafloride, is considered as a diffusion-controlled process
\[Br + Br \rightarrow Br_2\]
we have the viscosity of CF4 is 9.80 x 10-4 Nsm-2 at 30oC, what is the rate of recombination at 30oC?
S9.43a
Q9.43b
Calculate the rate constant of the diffusion-controlled reaction
\[ 2 I \rightarrow I_2 \]
in dichloromethane at 15°C, which has a viscosity of 0.449 mPa·s at 15°C.
S9.43b
1. Use equation 9.50 to calculate the rate constant.
\[ k_D = \dfrac{8}{3}\dfrac{RT}{\eta} \]
\[ k_D = \dfrac{8}{3} \dfrac{8.314 \dfrac{J}{mol \ K} \times 288\ K \times \dfrac{N\ m}{J}}{0.449\ mPa \ s \times \dfrac{Pa}{1000\ mPa} \times\dfrac{N/m^2}{Pa}} \times \dfrac{1000\ L}{m^3} \]
Answer:
\[ k_D = 1.42 \times 10^{10} M^{-1} s^{-1} \]
Q9.52
Japanese survivors have been exposed to the risk of radiation after the atomic bomb. One man was measured to have iodine-131 levels at 9.7 mC. Calculate the number of atoms of I-131 to which this radioactivity corresponds.S9.52
First, convert the rate mCi s-1
1 mCi=1.10X10-3 Ci
1 Ci=3.7 X 1010 s-1
The rate (\(r\) can be derived as such
\[r= (9.7\; Ci) \left( \dfrac{1\;Ci}{1000\; mCi} \right) \left( \dfrac{3.7 \times 10^{10}\; s^{-1}}{1\; Ci} \right) = 3.59 \times 10^8 s^{-1}\]
The accepted value for the half life of I-131 is 8.02 days. Using this information, the number of I-131 atoms can be calculated using the nuclear decay equation. Use the
Nuclear Decay Equation:
\[ \lambda N = \dfrac{\ln 2}{t_{1/2}} N\]
or
\[N = \dfrac{\ln 2}{t_{1/2}} r\]
The half-life for the radioactive beta decay of iodine is 8.02 days
\[\ce{^{131}_{53}I} \rightarrow \ce{^{131}_{54}Xe} + \beta + \bar{\nu_e} \]
therefore, the rate is
\[r= 3.59 \times 10^8 s^{-1}\]
Plug into the equation and convert days to seconds.Q9.54
Calculate the rate law for the following acid-catalyzed reaction:
\[CH_3COCH_3 + Br_2 \overset{H^+}{\longrightarrow} CH_3COCH_2Br + H^+ + Br^-\]
| Expt. # | \([CH_3COCH_3]_o\)/ M | \([Br_2]_o\) /M | \([H^+]_o\) /M | Rate of Disappearance Br2/ M*s-1 |
|---|---|---|---|---|
| 1 |
0.3 |
0.05 | 0.05 | \(5.7 \times 10^{-5}\) |
| 2 | 0.3 | 0.1 | 0.05 | \(5.7 \times 10^{-5}\) |
| 3 | 0.3 | 0.05 | 0.05 | \(1.2 \times 10^{-4}\) |
| 4 | 0.4 | 0.05 | 0.2 | \(3.1 \times 10^{-4}\) |
| 5 | 0.4 | 0.05 | 0.05 | \(7.6 \times 10^{-5}\) |
S9.54
Find the rate law.
rate = k[CH3COCH3]^x [Br2]^y [H+]^z
[exp 1] / [exp 5]:
5.7e-5 / 7.6e-5 = (0.30/0.40)^x (0.050/0.050)^y (0.050/0.050)^z
3/4 = (3/4)^x
x = 1
[exp 1] / [exp 2]:
5.7e-5 / 5.7e-5 = (0.30/0.30) (0.050/0.10)^y (0.050/0.050)^z
1 = (1/2)^y
y = 0
[exp 1] / [exp 3]:
5.7e-5 / 1.2e-4 = (0.30/0.30) (0.050/0.10)^z
19/40 = (1/2)^z
z ≈ 1
Use [exp 1] to find rate constant.
5.7e-5 M/s = k(0.30 M)(0.050 M)
k = 3.8e-3 M^(-1)-s^(-1)
"calculate the rate of disappearance of bromine if the initial concentration are .600mol/L, 0.200 mol/L, and .10 mol/L for propanone, bromine and H+."
rate = (3.8e-3 M^(-1)-s^(-1))(0.600 M)(0.10 M)
rate = 2.28e-4 M/s
Q9.55
Determine the rate law for the following reaction:
\[N_2O_2 + H_2 \rightarrow H_2O + N_2O\]
In addition, determine which of the following actions would alter the value of \(k\)?
- Increase in pressure of \(N_2O_2\)
- Increase in volume size of container
- Increase in temperature
- Addition of catalyst to the container.
- None of the above ;a rate constant is always constant.
Q9.56
Consider the mechanism for the association of iodine atoms to create molecular iodine.
\[2I_{(g)} \rightleftharpoons I_{2(g)}^*\]
\[I_2^*(g) + M(g) \rightarrow I_{2(g)} + M_{(g)}\]
With the respect of the first step is at equilibrium, determine the expected rate law (d/dt)[I2(g)] in terms of k1, k-1, k2, [I], and [M].
Q9.57
Consider the following reaction:
\[C_3H_{8(g)} + 5O_{2(g)} -> 3CO_{2(g)} + 4H_2O_{(g)}\]
If propane (C3H8) is burning at a rate of 0.15 M/s^-1, calculate the rate of formation of CO2.
9.4: More Complex Reactions
S9.57
First, express the reaction with the differential rate equation for the reactants and products involved.
-(d/dt)[C3H8] = (1/3)(d/dt)[CO2]
Then, use the given burning rate of propane and plug it into the differential equation.
(d/dt)[CO2] = 3(0.15M/s^-1)
9.5: The Effect of Temperature on Reaction Rates
Q9.26
If kept in a refrigerator, fresh fish will last for 3 days. If kept in a freezer, it will last for 6 months. Assuming that the temperature in the refrigerator is 5°C, and the temperature in the freezer is -10°C, calculate the activation energy for the bacterial spoiling of fish. Assume that the spoiling time is the 1/e lifetime instead of the half-life.
Q9.27
Find the activation energy of a reaction whose rate constant is multiplied by 6.50 when T is increased from 300.0 K to 310.0 K. For a reaction with Ea = 19 kJ/mol, by what factor is k multiplied when T increases from 300.0 K to 310.0 K?
Q9.28
The kinetics of the browning of juice from Golden Delicious apples was studied; at 20°C k=7.87×10-3/week, and at 37°C k=0.139/week. What is the activation energy for the browning of Golden Delicious apple juice?

