3.7: Bond Energies and Enthalpies
- Page ID
- 41418
In the absence of standard formation enthalpies, reaction enthalpies can be estimated using average bond enthalpies. This method is not perfect, but it can be used to get ball-park estimates when more detailed data is not available. A bond dissociation energy \(D\) is defined by
\[XY(g) \rightarrow X(g) + Y(g)\]
with \(\Delta H \equiv D(X-Y)\)
In this process, one adds energy to the reaction to break bonds, and extracts energy for the bonds that are formed.
\[\Delta H_{rxn} = \sum (\text{bonds broken}) - \sum (\text{bonds formed})\]
As an example, consider the combustion of ethanol:
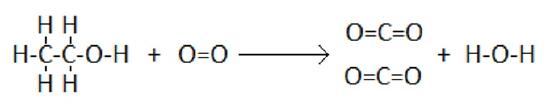
In this reaction, five C-H bonds, one C-C bond, and one C-O bond, and one O=O bond must be broken. Also, four C=O bonds, and one O-H bond are formed.
| Bond | Average Bond Energy (kJ/mol) |
|---|---|
| C-H | 413 |
| C-C | 348 |
| C-O | 358 |
| O=O | 495 |
| C=O | 799 |
| O-H | 463 |
The reaction enthalpy is then given by
\[ \begin{align} \Delta H_c = \, &5(413 \,kJ/mol) + 1(348\, kJ/mol) + 1(358 \,kJ/mol) \nonumber \\ & + 1(495\, kJ/mol) - 4(799 \,kJ/mol) – 2(463\, kJ/mol) \nonumber \\ =\,& -856\, kJ/mol \end{align}\]
Because the bond energies are defined for gas-phase reactants and products, this method does not account for the enthalpy change of condensation to form liquids or solids, and so the result may be off systematically due to these differences. Also, since the bond enthalpies are averaged over a large number of molecules containing the particular type of bond, the results may deviate due to the variance in the actual bond enthalpy in the specific molecule under consideration. Typically, reaction enthalpies derived by this method are only reliable to within ± 5-10%.
Contributors and Attributions
Patrick E. Fleming (Department of Chemistry and Biochemistry; California State University, East Bay)

