2.6: Kinetic Theory of Gases

The kinetic theory describes a gas as a large number of submicroscopic particles (atoms or molecules), all of which are in constant, random motion. The rapidly moving particles constantly collide with each other and with the walls of the container. Kinetic theory explains macroscopic properties of gases, such as pressure, temperature, viscosity, thermal conductivity, and volume, by considering their molecular composition and motion. The theory posits that gas pressure is due to the impacts, on the walls of a container, of molecules or atoms moving at different velocities.

The Model

The five basic tenets of the kinetic-molecular theory are as follows:

1. A gas is composed of molecules that are separated by average distances that are much greater than the sizes of the molecules themselves. The volume occupied by the molecules of the gas is negligible compared to the volume of the gas itself.
2. The molecules of an ideal gas exert no attractive forces on each other, or on the walls of the container.
3. The molecules are in constant random motion, and as material bodies, they obey Newton's laws of motion. This means that the molecules move in straight lines (see demo illustration at the left) until they collide with each other or with the walls of the container.
4. Collisions are perfectly elastic; when two molecules collide, they change their directions and kinetic energies, but the total kinetic energy is conserved. Collisions are not “sticky".
5. The average kinetic energy of the gas molecules is directly proportional to the absolute temperature. Notice that the term “average” is very important here; the velocities and kinetic energies of individual molecules will span a wide range of values, and some will even have zero velocity at a given instant. This implies that all molecular motion would cease if the temperature were reduced to absolute zero.

According to this model, most of the volume occupied by a gas is empty space; this is the main feature that distinguishes gases from condensed states of matter (liquids and solids) in which neighboring molecules are constantly in contact. Gas molecules are in rapid and continuous motion; at ordinary temperatures and pressures their velocities are of the order of 0.1-1 km/sec and each molecule experiences approximately 10¹⁰collisions with other molecules every second.

If gases do in fact consist of widely-separated particles, then the observable properties of gases must be explainable in terms of the simple mechanics that govern the motions of the individual molecules. The kinetic molecular theory makes it easy to see why a gas should exert a pressure on the walls of a container. Any surface in contact with the gas is constantly bombarded by the molecules.

Figure 2.6.1: When a molecule collides with a rigid wall, the component of its momentum perpendicular to the wall is reversed. A force is thus exerted on the wall, creating pressure. Image used with permisison from OpenSTAX

At each collision, a molecule moving with momentum mv strikes the surface. Since the collisions are elastic, the molecule bounces back with the same velocity in the opposite direction. This change in velocity ΔV is equivalent to an acceleration a; according to Newton's second law, a force f = ma is thus exerted on the surface of area A exerting a pressure P = f/A.

Kinetic Interpretation of Temperature

According to the kinetic molecular theory, the average kinetic energy of an ideal gas is directly proportional to the absolute temperature. Kinetic energy is the energy a body has by virtue of its motion:

\[ KE = \dfrac{mv^2}{2}\]

As the temperature of a gas rises, the average velocity of the molecules will increase; a doubling of the temperature will increase this velocity by a factor of four. Collisions with the walls of the container will transfer more momentum, and thus more kinetic energy, to the walls. If the walls are cooler than the gas, they will get warmer, returning less kinetic energy to the gas, and causing it to cool until thermal equilibrium is reached. Because temperature depends on the average kinetic energy, the concept of temperature only applies to a statistically meaningful sample of molecules. We will have more to say about molecular velocities and kinetic energies farther on.

• Kinetic explanation of Boyle's law: Boyle's law is easily explained by the kinetic molecular theory. The pressure of a gas depends on the number of times per second that the molecules strike the surface of the container. If we compress the gas to a smaller volume, the same number of molecules are now acting against a smaller surface area, so the number striking per unit of area, and thus the pressure, is now greater.

• Kinetic explanation of Charles' law: Kinetic molecular theory states that an increase in temperature raises the average kinetic energy of the molecules. If the molecules are moving more rapidly but the pressure remains the same, then the molecules must stay farther apart, so that the increase in the rate at which molecules collide with the surface of the container is compensated for by a corresponding increase in the area of this surface as the gas expands.

• Kinetic explanation of Avogadro's law: If we increase the number of gas molecules in a closed container, more of them will collide with the walls per unit time. If the pressure is to remain constant, the volume must increase in proportion, so that the molecules strike the walls less frequently, and over a larger surface area.

• Kinetic explanation of Dalton's law: "Every gas is a vacuum to every other gas". This is the way Dalton stated what we now know as his law of partial pressures. It simply means that each gas present in a mixture of gases acts independently of the others. This makes sense because of one of the fundamental tenets of KMT theory that gas molecules have negligible volumes. So Gas A in mixture of A and B acts as if Gas B were not there at all. Each contributes its own pressure to the total pressure within the container, in proportion to the fraction of the molecules it represents.

Derivation of the Ideal Gas Law

One of the triumphs of the kinetic molecular theory was the derivation of the ideal gas law from simple mechanics in the late nineteenth century. This is a beautiful example of how the principles of elementary mechanics can be applied to a simple model to develop a useful description of the behavior of macroscopic matter. We begin by recalling that the pressure of a gas arises from the force exerted when molecules collide with the walls of the container. This force can be found from Newton's law

\[f = ma = m\dfrac{dv}{dt} \label{2.1}\]

in which \(v\) is the velocity component of the molecule in the direction perpendicular to the wall and \(m\) is its mass.

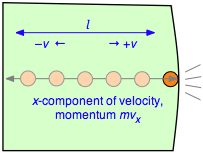
To evaluate the derivative, which is the velocity change per unit time, consider a single molecule of a gas contained in a cubic box of length l. For simplicity, assume that the molecule is moving along the x-axis which is perpendicular to a pair of walls, so that it is continually bouncing back and forth between the same pair of walls. When the molecule of mass m strikes the wall at velocity +v (and thus with a momentum mv ) it will rebound elastically and end up moving in the opposite direction with –v. The total change in velocity per collision is thus 2v and the change in momentum is \(2mv\).

After the collision the molecule must travel a distance l to the opposite wall, and then back across this same distance before colliding again with the wall in question. This determines the time between successive collisions with a given wall; the number of collisions per second will be \(v/2l\). The force \(F\) exerted on the wall is the rate of change of the momentum, given by the product of the momentum change per collision and the collision frequency:

\[F = \dfrac{d(mv_x)}{dt} = (2mv_x) \times \left( \dfrac{v_x}{2l} \right) = \dfrac{m v_x^2}{l} \label{2-2}\]

Pressure is force per unit area, so the pressure \(P\) exerted by the molecule on the wall of cross-section \(l^2\) becomes

\[ P = \dfrac{mv^2}{l^3} = \dfrac{mv^2}{V} \label{2-3}\]

in which \(V\) is the volume of the box.

As noted near the beginning of this unit, any given molecule will make about the same number of moves in the positive and negative directions, so taking a simple average would yield zero. To avoid this embarrassment, we square the velocities before averaging them

\[\bar{v^2} = \dfrac{v_1^2 + v_2^2 + v_3^2 + v_4^2 .. . v_N^2 }{N}= \dfrac{\sum_i v_i^2}{N} \]

and then take the square root of the average. This result is known as the root mean square (rms) velocity.

\[v_{rms} = \sqrt{ \bar{v^2}}\]

We have calculated the pressure due to a single molecule moving at a constant velocity in a direction perpendicular to a wall. If we now introduce more molecules, we must interpret \(v^2\) as an average value which we will denote by \(\bar{v^2}\). Also, since the molecules are moving randomly in all directions, only one-third of their total velocity will be directed along any one Cartesian axis, so the total pressure exerted by \(N\) molecules becomes

\[ P=\dfrac{N}{3}\dfrac{m \bar{\nu}^2}{V} \label{2.4}\]

Recalling that \(m\bar{v^2}/2\) is the average translational kinetic energy \(\epsilon\), we can rewrite the above expression as

\[PV = \dfrac{1}{3} N m \bar{v^2} = \dfrac{2}{3} N \epsilon \label{2-5}\]

The 2/3 factor in the proportionality reflects the fact that velocity components in each of the three directions contributes ½ kT to the kinetic energy of the particle. The average translational kinetic energy is directly proportional to temperature:

\[\color{red} \epsilon = \dfrac{3}{2} kT \label{2.6}\]

in which the proportionality constant \(k\) is known as the Boltzmann constant. Substituting Equation \(\ref{2.6}\) into Equation \(\ref{2-5}\) yields

\[ PV = \left( \dfrac{2}{3}N \right) \left( \dfrac{3}{2}kT \right) =NkT \label{2.7}\]

The Boltzmann constant k is just the gas constant per molecule. For n moles of particles, the Equation \(\ref{2.7}\) becomes

\[ PV = nRT \label{2.8}\]

which is the Ideal Gas law.

Contributors and Attributions

• Stephen Lower, Professor Emeritus (Simon Fraser U.) Chem1 Virtual Textbook