23.1: A Phase Diagram Summarizes the Solid-Liquid-Gas Behavior of a Substance
- Page ID
- 14497
A good map will take you to your destination with ease, provided you know how to read it. A map is an example of a diagram, a pictorial representation of a body of knowledge. In science they play a considerable role. Next to plots and tables diagrams are an important means of making information and/or theoretical knowledge accessible.
Constructing them takes quite a bit of thought. You want to represent as much of what you know and give as accurate a picture of it without conveying anything incorrect. If the drawing can be made to scale that makes it quite a bit more powerful, but this is not strictly necessary. A remark like not to scale or schematically does need to be given if applicable. A good caption or description is essential.
Thermodynamic Stability and Fluctuations
There are different kinds of equilibrium, besides the stable equilibrium that represents an absolute minimum in the \(G\) function. Of course \(G\) is potentially a function of a great number of variables, but let us look at a diagram in which \(G\) is shown as a function of only one unspecified variable. You could think of the density, the mole fraction of one of the components of a mixture or an applied electrical field or whatever, but the argument is general.
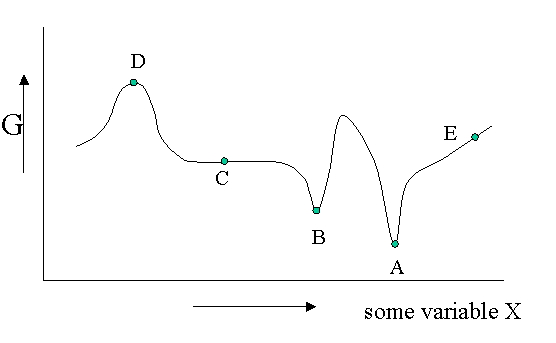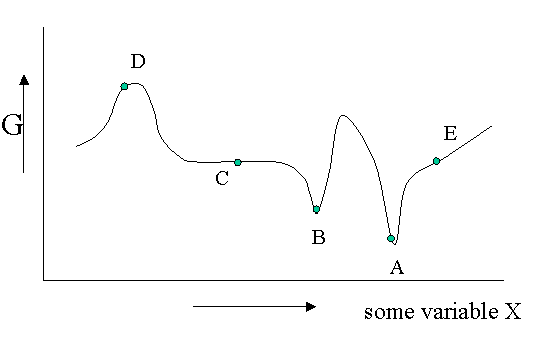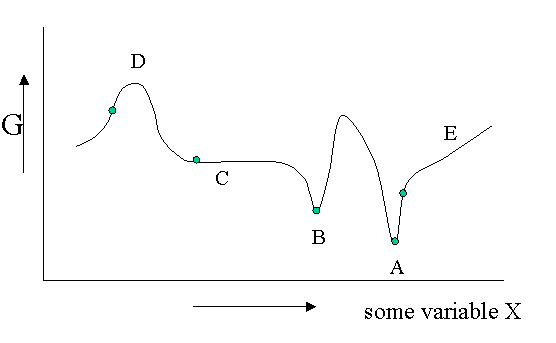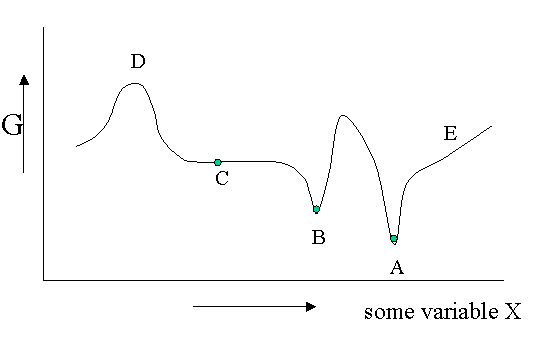
Figure 23.1.1 is helpful to point out that besides a stable equilibrium (\(A\)) there can also be an metastable equilibrium (B) or an indifferent equilibrium (\(C\)). The local derivatives of \(G\) (versus all variables of which we only show one) are zero in all three cases, which means that changes in the variables are not spontaneous. For a labile equilibrium (\(D\)) the opposite is true. Any small deviation will make the system role down hill. (Note that the second derivative has the opposite sign compared to cas A) and B)) A labile equilibrium is seldom or never observed except in a circus where artists delight in balancing objects on their heads (because you pay for it).. This usually requires continuous small corrections to maintain the precarious balance. All other points in our diagram represent state of instability because locally \(dG\) is not zero and a spontaneous process can take place.
The fact that \(dG=0\) in the equilibrium points does not mean small deviations from the minimum cannot happen at times. We have seen e.g. that the Boltzmann distribution was simply the most likely distribution. The most likely one is the one that has the highest number of realizations W. Another way of saying that is that it is the one with the highest entropy S. A slightly less likely distribution may occur from time to time by chance. It will have a little less entropy, but the same \(\langle E \rangle\). That means it will have a slightly higher \(G\) (\(G=H-TS\)). From time to time therefore \(G\) will fluctuate a bit. Such fluctuations are very small for large systems, but they are of greater relative importance for small systems (like a nanoparticle). (Statistical averaging works best on large ensembles.)
The fluctuations in \(G\) mean that small fluctuations in its variables like density etc. can also occur. They are usually kept in check, because \(dG\) is no longer zero when moving away from the equilibrium state. This drives the system back to the minimum spontaneously. You could picture the system wobbling a bit around in its G-well. This holds for stable and metastable equilibria alike.
In the indifferent case (\(C\)) however the derivative is zero (or very close to zero) for a range of neighboring values of some variable. In contrast to \(A\) and \(B\) also the second derivative is zero. This means that there is little penalty to much larger deviations in the variable. If this variable is the density the system becomes milky and shows opalescence a strong scattering of light because the refractive index depends on the strongly fluctuating density. This is observed near critical points and is called critical opalescence.
Unary Phase Diagrams
A unary phase diagram summarizes the equilibrium states of a single pure substance. We will see that we can also look at mixtures of two components (binary diagrams) or more (ternary, quaternary, quinary, senary etc.). Usually a phase diagram only maps out stable equilibria, but occasionally metastable ones may be given too (e.g., with a dashed line).
Liquid-Vapor Equilibrium Curve
We have seen that the Gibbs function \(G\) depends strongly (logarithmically) on pressure for a gas, but only slightly (and linearly) for a liquid. The two curves intersect in a point representing the equilibrium vapor pressure of the liquid. At lower pressures the vapor is more stable, at higher ones the liquid. (For a solid the same holds as for the liquid). This means that except at the intersection point we only will observe one phase.
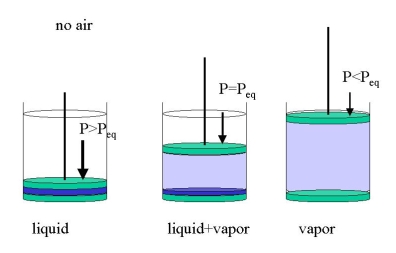
It is important to stress that this holds in the absence of other matter, e.g., when we put only water into an evacuated cylinder (Figure 23.1.2 ). We may get three cases:
- we compress the cylinder until it only contains the liquid under hydrostatic pressure (\(P>P_{eq}\))
- we expand the cylinder until all water has vaporized (\(P<p_{eq}\))>
- we let part of the water evaporate, just enough so that the space above the liquid is filled with an equilibrium vapor pressure (\(P=P_{eq}\))
At room temperature \(P_{eq}\) for water is only about 15 Torr. If we apply 1 bar -or let the atmosphere do the job- we will only have liquid water. If other gases are present, e.g., air, we must distinguish between the total pressure (e.g., 1 bar) and the equilibrium vapor pressure which will now be the partial pressure. In a cylinder with water and one bar of air just enough water will evaporate to establish equilibrium. The evaporation will be limited to the gas-liquid interface unless the partial pressure equals the total pressure. Then the liquid will boil.
(Do allow the volume to expand, though., why? If the volume is constant the pressure builds up and boiling will stop.
If we consider the set of equilibrium pressures as a function of temperature and plot that in a P vs. T diagram we have one component of our phase diagram.
Gas-solid Equilibrium Curve
For solids the situation is similar as the \(G(P)\) curve is once again an almost flat straight line. The intersection with the logarithmic curve for the gas will define an equilibrium pressure for gas-solid co-existence. Generally vapor pressures above solids are quite small, but not negligible. As for liquids we can construct a line representing the equilibrium pressures for sublimation as function of temperature and add it to the phase diagram.
Liquid-solid Equilibrium Curve
The \(\text{solid} \rightleftharpoons \text{liquid}\) equilibrium is known as melting or freezing is not very dependent on pressure. Usually melting points increase a little bit with pressure, although water is a peculiar exception. It expands upon freezing and the melting point goes down (a bit) with pressure. In our diagram this will represent an almost vertical line leaning a little forwards for most substances, but backwards for water and a few others.
Putting the Curve Together
The three lines come together in the triple point, the only point where all three phases are at equilibrium with each other. For water, its temperature is only 0.01 K different from the normal melting point (273.16 K) and its pressure is only 4.58 Torr. The intersection points with a line representing atmospheric pressure give the melting and boiling points at that pressure.
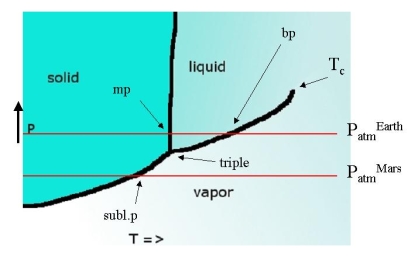
If the triple point lies above the line that represents atmospheric pressure this implies that a liquid is never observed. On earth CO2 is such a substance. The intersection of the solid-vapor equilibrium line with the 1 bar line represents a state where the solid will 'boil' (evaporate from inside out). This is known as the sublimation point. The melting points at P=1 bar are known as the standard melting point, the only slightly different one at 760 Torr = 1 atm is called normal melting point. The same goes for boiling and sublimation points.
There is nothing magical about \(P=1 \,bar\). It just happens to be the pressure of our home planet. On a planet with higher atmospheric pressures \(CO_2\) may well be a liquid and on such a planet, all boiling points will be quite different (higher than on earth). The melting points will also differ, but only slightly so. On Mars where atmospheric pressure is much lower water can not occur in liquid form, much like carbon dioxide on earth - it sublimes.
We should also realize that in a closed container (glass ampoule, hermetically sealed DSC pan), we can observe melting points at only very slightly different temperature values, but we will not see a boiling effect. Why?
To see a boiling point the container must be open to the (constant!) 1 bar pressure of the earths atmosphere that defines it and causes the boiling phenomenon. If the ampoule is sealed it will generate its own (autogenous) pressure, depending on what you put in, how much of it in relation to the volume, how volatile it is and the temperature. The autogenous pressure does not interfere with the melting point much (the melting line is almost vertical), but as \(P\) changes with temperature you may never reach boiling conditions.
In DSC experiments it is possible to observe boiling points only if the pan has been carefully perforated with a hole of known size. It must be big enough that the pressure inside the pan does not build up above atmospheric, but small enough that it does not cause premature loss of mass during the run. The latter spoils the calculation of the intensive value (per mole, per gram) of the heat of vaporization.
The liquid evaporation line ends in a point that we have encountered before: the critical point \(T_C\). As temperature increases the liquid and vapor phases in equilibrium with each other start to resemble each other more and more and at \(T_c\) they coalesce. At this point the liquid-gas equilibrium becomes indifferent with respect to density and large fluctuations occur leading to critical opalescence.
Notice that there is a relationship of dimensionality between the objects in the diagram and the number of phases present:
- 2 D planes: one phase
- 1 D curves: two phases
- 0 D point: three phases
As you see the sum is always three.
Number of moles
So far we have typically considered one substance at the time, but for chemists it is imperative to deal with more than one because we are typically changing one into the other in our reactions. This means that the number of moles \(n\), that we often simply set equal to one now becomes an important variable in its own right. Besides we will actually have two (or more) of them: the number of moles of component one and the one for the other component. This makes n a much less trivial variable.
This is already the case at a simple melting point, say when ice melts, because we are dealing with changing quantities of ice and water:
\[n_{ice} + n_{water} = n_{total} \nonumber \]
If all we do is turn water into ice or vice versa, we have \(dn_{total}=0\), so that:
\[dn_{ice} =- dn_{water} \nonumber \]
To deal with changing n's, we need to expand our mathematical notation a bit.
Partial variables
So far we have simply divided our thermodynamic functions if they were extensive by the number of moles and arrived at intensive molar values:
\[G_{molar} = \dfrac{G}{ n} \nonumber \]
\[V_{molar} = \dfrac{V}{n} \nonumber \]
We have written such intensive molar values by writing a bar over the symbol G or V. We should note that scaling the function this way departs from the assumption that the function \(G\) depends on the variable n as a straight line that passes through the origin.
If we have the same pure compound in two phases, like ice and water we can still apply this principle and write:
\[G_{molar}^{ice} = \dfrac{G^{ice}}{n^{ice}} \nonumber \]
\[V_{molar}^{ice} = \dfrac{V^{ice}}{n^{ice}} \nonumber \]
\[G_{molar}^{water} = \dfrac{G^{water}}{n^{water}} \nonumber \]
\[V_{molar}^{water} = \dfrac{V^{water}}{n^{water}} \nonumber \]
If we have a mixture of two substances present as \(n_1\) and \(n_2\) moles the dependency need not be linear on either if the two substances interact with each other. This is also true for function like the volume of a liquid mixture. In the presence of interactions volumes do not have to be linearly additive. We can define a partial molar value of e.g. for the volume:
\[V_{partial molar,1} = \dfrac{\partial V}{\partial n_1} \nonumber \]
at \(n_2\) = constant
\[V_{partial molar,2} = \dfrac{\partial V}{\partial n_2} \nonumber \]
at \(n_1\) = constant
The notation of putting a bar over the \(V\) symbol is used for these partial quantities as well. Partial molar volumes have been measured for many binary systems. They are functions of the composition (mole fraction) as well as the temperature and to a lesser extent the pressure.
The partial molar Gibbs free energy (\(\left(\dfrac{∂G}{∂n_i}\right)_{P,T}\), all other n's) is denoted with \(μ\) and is called the thermodynamic potential.
When numbers of moles can change we can write the corresponding change in \(G\) as:
\[dG = -SdT + VdP + \sum_i^N \left( \dfrac{\partial G}{\partial n_1} \right)_{P,T,n_{j\neq i}}dn_i \nonumber \]
\[dG = -SdT + VdP + \sum_i^N μ_idn_i \nonumber \]
over \(N\) phases in the system. As you can see we are adding a set of conjugate variables \(μ_in_i\) for each phase \(i\). If we are considering a pure component (but in different modifications, like ice and steam), we can still write:
\[ μ_i = \left( \dfrac{\partial G}{\partial n_1} \right)_{P,T,n_{j\neq i}} = \dfrac{G_i}{n_i} \nonumber \]
As soon as we are dealing with mixtures we really do have derivatives.

