18.10: Ortho and Para Hydrogen
- Page ID
- 57614
The molecules of hydrogen can exist in two forms depending on the spins on the two hydrogen nuclei. If both the nuclear spins are parallel, the molecule is called ortho and if the spins are antiparallel, it is referred to as para (in disubstituted benzene, para refers to the two groups at two opposite ends, while in ortho, they are adjacent or “parallel” to each other). The spin on the hydrogen nucleus has a magnitude of \(½ ħ\). The presence of nuclear spins leads to very interesting consequences for the populations of the rotational states and on a macroscopic scale, has consequences on measured entropies and heat capacities as well. The total partition function of \(\ce{H_2}\) can be written as:
\[q_\text{tot} = q_\text{elec} q_\text{vib} q_\text{rot} q_\text{trans} q_\text{nuc} \nonumber \]
where, the subscripts refer to the respective motions. After “half” a rotation, the nuclei are superimposed on each other. Since a proton is a spin half nucleus, the total wave function must be antisymmetic with respect to the exchange of the particles. i.e.:
\[ \psi(1,2) = - \psi (2,1) \nonumber \]
The translational motion refers to the motion of the molecular center of mass and has no influence on the symmetry of the nuclear wave function. Vibrational motion depends on the magnitude of the internuclear distance and has no effect on the particle exchange. The electronic motion also has no effect on the symmetry properties of the nuclear wave function. Therefore, the product of the nuclear spin and rotational wave functions must be antisymmetric with respect to the particle exchange. For the nuclear spin functions, there are four combinations. One combination is a singlet:
\[ | \psi_{\nu,s} \rangle = \alpha(1) \beta(2) - \alpha (2) \beta (1) \nonumber \]
And the other three combinations are the three states of a triplet:
\[ \begin{align*} | \psi_{\nu,s} \rangle &= \alpha(1) \alpha(2) \\[4pt] | \psi_{\nu,s} \rangle &= \alpha(1) \beta(2) + \alpha (2) \beta (1) \\[4pt] | \psi_{\nu,s} \rangle &= \beta(1) \beta(2) \end{align*} \]
The rotational wavefunctions (\(ψ_r\)) are given in terms of the associated Legendre polynomials \(P^{|m|}_l (x)\) where \(x = \cos θ\):
\[ | ψ_r \rangle = e^{im\phi} P^{|m|}_l (\cos \theta) \label{3.91} \]
with:
\[\begin{align} P_{l}^{(m)}(x) &=\left(1-x^{2}\right)^{| m / 2} \frac{d^{|m|} P_{l}(x)}{d x^{m |}} \\[4pt] \quad P_{l}(x) &=\frac{1}{2^{l} l !} \frac{d^{l}\left(x^{2}-1\right)^{l}}{d x^{l}} \label{3.92} \end{align} \]
When the nuclei are interchanged, \(θ\) becomes \(π - θ\) and \(φ\) is changed to \(φ + π\). The polynomials change as:
\[P_{l}(-x)=(-1)^{\prime} P_{l}(x) ; \quad P_{l}^{|m|}(-x)=(-1)^{l-|m|||} P_{l}^{|m|}(x) \label{3.93} \]
The exponential function changes as:
\[e^{i m(\phi+\pi)}=e^{i m \pi} e^{i m \varphi}=(-1)^{|m|} e^{i m \varphi} \label{3.94} \]
Therefore, the rotational wave function changes as:
\[ \begin{align} P_l(-x) &= (-1)^l P_l(x) \\[4pt] P^{|m|}_l(-x) &= (-1)^{l-|m|} P^{|m|}_l(x) \label{3.95} \end{align} \]
- \( | \psi_r \rangle\) is symmetrical for even \(J\), and
- \( | \psi_r \rangle\) is antisymmetrical for odd \(J\)
Combining the nuclear spin and the rotational parts, we see that, the product \(\psi_{r}, \psi_{m}\) must be antisymmetrical (with respect to the exchange of nuclei) for half integral nuclear spins and symmetrical for integral spins. To accomplish this, the singlet nuclear states (para) must be combined with the even rotational functions and the triplet nuclear states must be combined with the odd rotational states. The rotational partition functions for ortho and para hydrogens are, thus:
\[q_{\text{ortho}}=q_{\nu, t} q_{r, \text{odd}}=3 \sum_{J=1,3,5, \ldots}(2 J+1) e^{-J(J+1) \Theta_{R} / T} \label{3.97} \]
and:
\[q_{\text{para}}=q_{\text {\nu,s }} q_{r, \text{even}}=1 \sum_{J=0,2,4, \ldots}(2 J+1) e^{-J(J+1) \Theta_{R} / T} \label{3.98} \]
where \(Θ_R\) is the rotational temperature defined previously. The total partition function consisting both ortho and para hydrogens is given by:
\[q_{\text{rot}, nu}=1 \sum_{j=0.2 .4}(2 J+1) e^{-J(J+1) \Theta_{k} / T}+3 \sum_{j=1,3,5, n}(2 J+1) e^{-J(J+1) \Theta_{R} / T} \label{3.99} \]
The ratio of ortho to para hydrogens at thermal equilibrium is given by:
\[\frac{N_{o}}{N_{p}}=\frac{3 \sum_{j=1,2,3 \ldots}(2 J+1) e^{-J(J+1) \Theta_{R} / T}}{\sum_{j=0} 2(2 J+1) e^{-J(J+1) \Theta_{R} / T}} \label{3.100} \]
At high temperature, the two summations become equal and therefore, the high temperature limit of \(N_{o} / N_{p}\) is 3. At low temperature, the ratio becomes:
\[\frac{N_{o}}{N_{p}}=\frac{3\left(3 e^{-2 \Theta_{k} / T}+\ldots \ldots\right)}{1\left(1+5 e^{-5 \Theta_{n} / T} + \ldots \right)} \rightarrow 0, \text { as } T \rightarrow 0 \label{3.101} \]
A good experimental verification of the above analysis is a comparison between the calculated rotational heat capacities at constant volume (\(C_V\)) rot, nu (calculated from:
\[C_V= \dfrac{\partial \langle E \rangle }{\partial T} \nonumber \]
where:
\[\langle E \rangle = \dfrac{\partial \ln q_{\text{rot},\nu} }{\partial \beta} \nonumber \]
The heat capacities are shown as a function of temperature in Figure 18.10.1 .
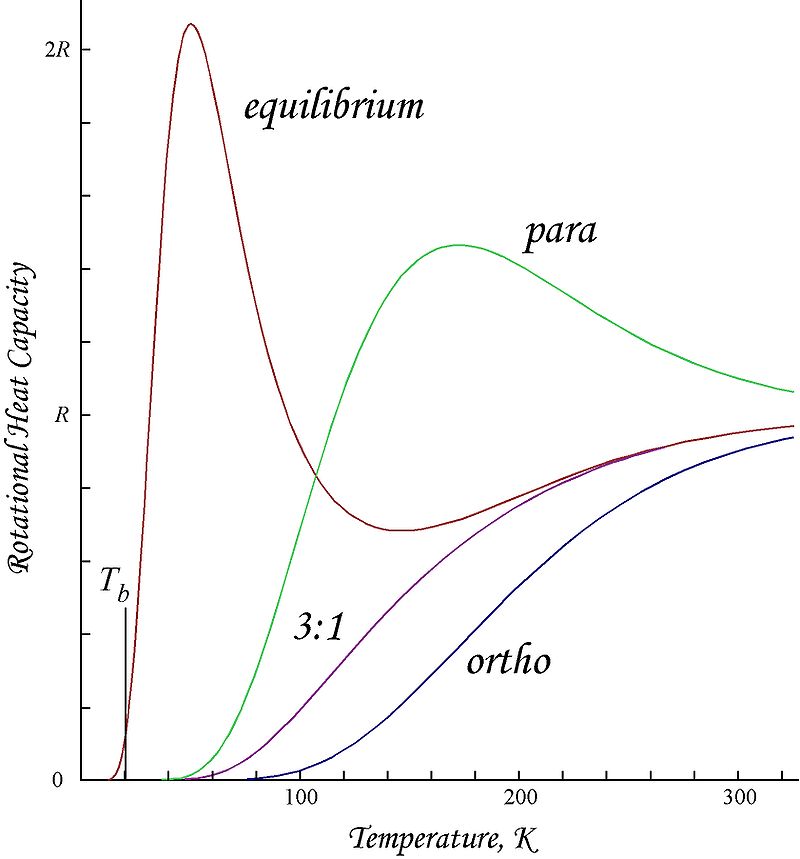
The purple curve marked 3:1 gives the experimental data, the curve eq represents the data for an equilibrated mixture of o- and p- at a given temperature. The curves o- and p- represent the heat capacities of pure o- and pure p- hydrogens calculated from the o- and p- partition functions given by Equations \(\ref{3.97}\) and \(\ref{3.98}\) respectively. Initially it was a puzzle as to why the experimental data differs from the calculated values. In fact, the experimental data seemed to agree very well with the following equation:
\[ (C_V)_{\text{rot},\nu} = \dfrac{3}{4} (C_V)_{\text{rot},\nu} (\text{ortho}) + \dfrac{1}{4} (C_V)_{\text{rot},\nu} (\text{para}) \label{3.102} \]
The reason for this is that, when \(\ce H_2\) is cooled down from a higher temperature, the ortho:para ratio continues to remain 0.75 / 0.25 (the high temperature value) because the \(\text{ortho} \rightarrow \text{para}\) interconversion rate is very very small and we do not reach the equilibrium composition unless a catalyst such as activated charcoal is added to the gas mixture. Equation \(\ref{3.102}\) corresponds to a “frozen high temperature mixture” of ortho:para hydrogens. In the presence of the catalyst, the experiments also give the curve labeled as eq in the graph. This in indeed a very nice case where the experiments support not only the methods of statistical thermodynamics but also of the antisymmetry principle for bosons and fermions. If we consider the case of \(\ce{^{16}O2}\), where the nuclear spins are zero, the rotational wave function has to be symmetric as only symmetric wave functions are permitted for bosons. Thus, only even rotational states contribute to the partition function:
\[ q_{\text{rot}, V} (^{16}\ce{O_2}) = \sum_{J=0,2,4,\ldots} (2J+1) e^{-J(J+1) \theta_R/T} \nonumber \]
Contributors and Attributions
- www.chem.iitb.ac.in/~bltembe/pdfs/ch_3.pdf

