11.E: Computational Quantum Chemistry (Exercises)
- Page ID
- 13482
These are homework exercises to accompany Chapter 11 of McQuarrie and Simon's "Physical Chemistry: A Molecular Approach" Textmap.
What is meant by the expression ab initio calculation?
List all the terms in a complete molecular Hamiltonian.
Why are calculations on closed-shell systems more easily done than on open-shell systems?
How is it possible to reduce a multi-electron Hamiltonian operator to a single-electron Fock operator?
Why is the calculation with the Fock operator called a self-consistent field calculation?
What is the physical meaning of a SCF one-electron energy?
Why is the nonlinear variational method not used in every case to optimize basis functions, and what usually is done instead?
Why is it faster for a computer to use the variational principle to determine the coefficients in a linear combination of functions than to determine the parameters in the functions?
Identify the characteristics of hydrogenic, Slater, and Gaussian basis sets.
What is meant by the Hartree-Fock wavefunction and energy?
What is neglected that makes the Hartree-Fock energy necessarily greater than the exact energy?
What is meant by correlation energy?
What purpose is served by including configuration interaction in a calculation?
Q11.1
Prove that a three dimensional Gaussian function centered at \(r_1\) = \(x_1\)i + \(y_1\)j + \(z_1\)k is a product of three one-dimensional Gaussian functions centered on \(x_1\), \(y_1\), \(z_1\).
S11.1
\(e^{-a(r-r_0)^2}\) = \(e^{-a[(x-x_1)i+(y-y_1)j+(z-z_1)k]^2}\)
= \(e^{-a[(x-x_1)^2+(y-y_1)^2+(z-z_1)^2]}\)
= \(e^{-a(x-x_1)^2}\) \(e^{-a(y-y_1)^2}\) \(e^{-a(z-z_1)^2}\)
Q11.2
Show that
\[ \int_{0}^{\infty} e^{-(x-x_0)^2} dx = \int_{0}^{\infty} e^{-x^2} dx = \frac{1}{2}\int_{-\infty}^{\infty} e^{-x^2} dx = \sqrt{\pi} \]
S11.2
The equalities are all equivalent since in the first integral \( x_0\) is a constant and the second and third are even.
Q11.3
The Gaussian Integral \[I_{0} = \int^\infty_{-\infty} e^{-4x^2}dx \]
Convert the integration variables from Cartesian coordinates to polar coordinates and show that \[I_{0} = \dfrac{\sqrt{\pi}}{2}\]
S11.3
We first write
\[I^2_{0} = \left( \int^\infty_{-\infty} e^{-4x^2}dx \right)^2 = \int^\infty_{-\infty} e^{-4x^2}dx \int^\infty_{-\infty} e^{-4y^2}dy \]
the product of two integrals can be expressed as a double integral
\[I^2_{0} = \int^\infty_{-\infty} \int^\infty_{-\infty} e^{-4(x^2 + y^2)}dxdy \]
In polar coordinates \(x^2 + y^2 = r^2\) and \(dxdy = rdrd\theta \). The limits of integration in polar coordinates corresponding to the limits in Cartesian coordinates are 0 \(\le r < \infty\) and \(0 \le \theta \le 2\pi\).
The double integral becomes
\[I^2_{0} = \int^\infty_{0} \int^{2\pi}_{0} e^{-4r^2}rdrd\theta = 2\pi \int^{\infty}_{0} e^{-4r^2}rdr .\]
The integration over \(\theta\) gives a factor of \(2\pi\).The integral over r can be done using a U substitution, \( u = 4r^2 \) and \(du = 8rdr \).
Therefore
\[\int^{\infty}_{0} e^{-4r^2}rdr = \dfrac{1}{8} \int^{\infty}_{0} e^{-u^2}du = \dfrac{1}{8} \]
meaning that \( I^2 = 2\pi \times \dfrac{1}{8} \), so \(I_{0} = \dfrac{\sqrt{\pi}}{2}\).
Q11.4
Show that the integral
\(I_{2n}=\int_{-\infty}^{\infty} x^{2n}e^{-ax^2}dx\)
can be obtained from \(I_{o}\)
\(I_{o}=\int_{-\infty}^{\infty} e^{-ax^2}dx\)
by differentiating \(n\) times with respect to \(a\) when \(I_{o}\) is
\(\ I_{0}=\frac{1}{2}\big(\frac{\pi}{a}\big)^{\frac{1}{2}}\)
gives in a general form:
\(I_{2n}=\frac{1\cdot3\cdot5\cdots\big(2n-1\big)}{2^{n+1}a^{n}}\big(\frac{a}{2}\big)^{\frac{1}{2}}\)
S11.4
The first step is to take the derivative of \(I_{o}\) about 3 times with respect to \(a\):
\(I_{o}=\int_{-\infty}^{\infty} e^{-ax^2}dx\)
\(\frac{dI_{o}}{da}=\int_{-\infty}^{\infty} -x^{2}e^{-ax^2}dx=-\int_{-\infty}^{\infty} x^{2}e^{-ax^2}dx\)
\(\frac{d^2I_{o}}{da^2}=\int_{-\infty}^{\infty} -x^{2\cdot2}e^{-ax^2}dx=\int_{-\infty}^{\infty} x^{4}e^{-ax^2}dx\)
solve the integrals for the first \(I_{2n}\) starting with \(I_{o}\),
\(I_{o}=\int_{-\infty}^{\infty} e^{-ax^2}dx = \frac{1}{2} \big(\frac{\pi}{a}\big)^{\frac{1}{2}}\)
\(I_{2}=\int_{-\infty}^{\infty} x^{2}e^{-ax^2}dx=\frac{dI_{o}}{da}=\frac{1}{4a}\big(\frac{\pi}{a}\big)^{\frac{1}{2}}\)
\(I_{4}=\int_{-\infty}^{\infty} x^{4}e^{-ax^2}dx=\frac{d^2I_{o}}{da^2}=-\frac{dI_{2}}{da}=\frac{3}{8a}\big(\frac{\pi}{a}\big)^{\frac{1}{2}}\)
\(I_{6}=\int_{-\infty}^{\infty} x^{6}e^{-ax^2}dx=-\frac{d^3I_{o}}{da^3}=-\frac{dI_{4}}{da}=\frac{3\cdot5}{16a}\big(\frac{\pi}{a}\big)^{\frac{1}{2}}\)
in general
\(I_{2n}=\frac{1\cdot3\cdot5\cdots\big(2n-1\big)}{2^{n+1}a^{n}}\big(\frac{a}{2}\big)^{\frac{1}{2}}\)
(note: if you look at the equations sheet provided in the Gaussian integrals sections the limits of integration from -\(\infty\) to +\(\infty\) and from 0 to +\(\infty\) give the same end result with a minor difference in the exponent for the two in the denominator)
Q11.17
Using the Figure below, specify the coordinates of the atoms that comprise the molecule methane. Determine a set of Cartesian coordinates of the atoms in the molecule. The HCH bond angle is 110.0° and the C-H bond length is 109.1 pm.
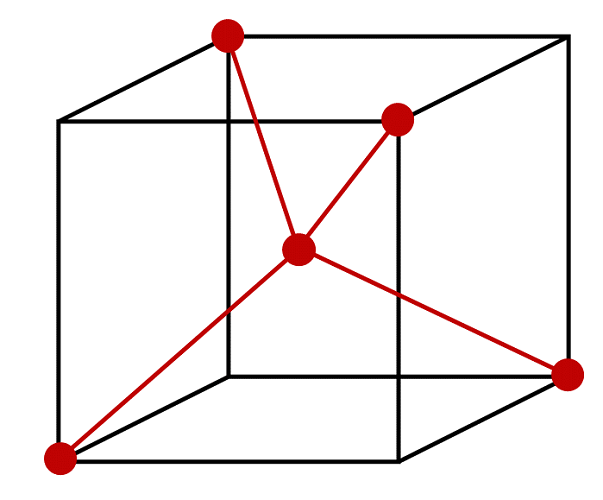
S11.17
This figure can represent methane if and only if the central atom is carbon and the 4 atoms at the vertices are hydrogen atoms. We then must assign the origin of our coordinate system to be at the carbon atom. Considering the length of the edge of this cube is 2a, then the bond length from the vertices (hydrogen atoms) to the center (carbon atom) is \( {\sqrt{3}} \) times the length of one edge of the cube, so
\[ \dfrac{109.1\; pm}{ \sqrt{3}} = 63 \; pm = a\]
Diagonal of cube length 2a would be \(2a\sqrt(3)\) - but we need half that.
Q11.18
Determine a rough set of Cartesian coordinates of the atoms in the molecule \(SiH_{3}F\) given the bond angle of \(H-Si-H\) is \(109.5^{\circ}\) and the \(Si-H\) and \(Si-F\) bond lengths are \(146.0\) and \(159.5 \hspace{.1cm} pm\), respectively. (Hint: locate the origin at the Silicon.)
S11.18
For a simpler case of \(SiH_{4}\), The four hydrogen would be equally far from the central atom (origin). The coordinates can be calculated as \( (a,a,a) \) ,\( (-a,-a,a) \),\( (a,-a,-a) \), and \( (-a,-a,-a) \). The value of \(a\) can be determined by \( a = \dfrac{l}{\sqrt{3}}\) where \(l\) is the bond length. For hydrogen:
\[a = \dfrac{146 \hspace{.1cm} pm}{\sqrt{3}} = 84.29 \hspace{.1cm} pm\]
For florine:
\[a = \dfrac{159.5 \hspace{.1cm} pm}{\sqrt{3}} = 92.09 \hspace{.1cm} pm\]
One set of solutions is:
| x/pm | y/pm | z/pm | |
|---|---|---|---|
| C | 0 | 0 | 0 |
| H | 84.29 | 84.29 | 84.29 |
| H | -84.29 | -84.29 | 84.29 |
| H | 84.29 | -84.29 | -84.29 |
| F | -92.09 | -92.09 | -92.09 |
Q11.19
| Molecule | Frequency [cm-1] | Re [pm] |
|---|---|---|
| H2 | 4647 | 73.2 |
| CO | 2438 | 111.4 |
| HCl | 2886 | 130 |
Given the above table of calculated vibrational frequencies and bond lengths, calculate the vibrational force constant of each of the molecules. Do you expect that the calculated values are higher or lower than the experimental values? Are bond length calculations or vibrational-frequency calculations more accurate? Why?
S11.19
The relationship between wave number and harmonic force constant can be expressed as
\[\tilde{\nu} = (2c\pi)^{-1} \sqrt{\dfrac{k}{\mu}}\]
which can be rewritten as
\[k=4\mu(\tilde{\nu}c\pi)^2.\]
The reduced masses can be found to be
\(\mu_{H_2} = 8.38\times10^{-28}\)kg, \(\mu_{CO} = 1.14\times10^{-26}\)kg, and \(\mu_{HCl} = 1.626\times10^{-27}\)kg.
Now we can find our force constants by plugging in the given values.
- \(k_{H_2} = 642 N/m\)
- \(k_{CO} = 2404 N/m\)
- \(k_{HCl} = 481 N/m\)
We should expect that the values we found are higher than what is experimentally measured, as other forces are unaccounted for. Bond length calculations are more accurate because it requires a smaller basis set to calculate accurately.
Q11.20
Normalize the following Gaussian function:
\[ \phi(r) = xe^{-\alpha r^{2}}\]
S11.20
We write \(\phi (r)\) in spherical coordinates and then apply the normalization condition of the normalized function \(A\phi (r)\)
The normalization condition is
\[ \int A^{2}x^{2}e^{-2\alpha r^{2}} d\tau = 1\]
or in bra-ket notation
\(\langle \phi(r) | \phi(r) \rangle = 1\).
where A is the normalization constant. In spherical coordinates,
\[ 1 = \int A^{2}r^{2} \sin ^{2}\theta\cos^{2}\phi e^{-2\alpha r^{2}} d\tau \]
\[ = A^{2} \int_{0}^{\infty} r^{4}e^{-2\alpha r^{2}} dr \int_{0}^{\pi} \sin^{3}\theta d\theta \int_{0}^{2\pi} \cos^{2}\phi d\phi \]
\[ \dfrac{1}{A^{2}} = \dfrac{3}{8(2\alpha)^{2}} \Big(\dfrac{\pi}{2\alpha}\Big)^{1/2} \Big(\dfrac{4}{3}\Big) (\pi) \]
\[ = \dfrac{\pi^{3/2}}{2^{7/2}\alpha^{5/2}} \]
Therefore, the nomalization constant will the inverse of this result:
\[ A = \Big(\dfrac{128\alpha^{5}}{\pi^{3}}\Big)^{1/4} \]
Q11.21
Which hydrogen atomic orbital corresponds to the following normalized Gaussian orbital?
\[ G(x, y, z; \alpha) = \Big(\dfrac{128\alpha^{5}}{\pi^{3}}\Big)^{0.25}ye^{-\alpha r^2}\]
How many radial and angular nodes does the above function have? Is this result what you would expect for the corresponding hydrogen function?
S11.21
The typical form is:
\[G_{nlm}(r, \theta, \phi) = N_{n}r^{n-1}e^{-\alpha r^{2}}Y_{l}^{m}(\theta, \phi)\].
From this, we can see the function in the question shows n = 2 and l = 1. Because n = 2, there is 1 node and l = 1 tells us that there is 1 angular node. Therefore, there are no radial nodes.This is consistent with the \(2p_{y}\) orbital in a hydrogenic function.
Q11-22
Slater type orbitals have the form, $$\chi_{nlm} = R_{n}(r)Y_{lm}(\theta,\phi)$$ where the second term is the spherical harmonic given by
$$R_{n}(r)= \frac{(2\alpha)^{(n+1/2)}}{\sqrt{(2n)!}} r^{(n-1)}e^{(-\alpha r)}$$
Define the 1s-slater type orbital.
S11-22
For n=1, the slater-type orbital is
$$\phi_{nlm}= \frac{(2\zeta)^{(n+1/2)}}{\sqrt{(2n)!}} r^{(n-1)}e^{(-\zeta r)}Y_{lm}(\theta,\phi)$$
$$\phi_{1s}(r,\zeta) = S_{100}(r,\zeta) = \sqrt{\frac{\zeta^3}{\pi}} e^{-\zeta r}$$
11.23
Consider the normalized functions
$$G_{1}(x, y, z; \alpha) = (\frac{2048\alpha^7}{9\pi^3})^(\frac{1}{4})x^2e^(-\alpha r^2)$$
$$G_{2}(x, y, z; \alpha) = (\frac{2048\alpha^7}{9\pi^3})^(\frac{1}{4})y^2e^(-\alpha r^2)$$
$$G_{3}(x, y, z; \alpha) = (\frac{2048\alpha^7}{9\pi^3})^(\frac{1}{4})z^2e^(-\alpha r^2)$$
$$G_{4}(x, y, z; \alpha) = (\frac{2048\alpha^7}{9\pi^3})^(\frac{1}{4})(x^2-y^2)e^(-\alpha r^2)$$
Which hydrogen atomic orbital corresponds to the linear combination
$$G_{3}(x, y, z; \alpha) +G_{1}(x, y, z;\alpha)?$$
S11.23
$$G_{3}(x, y, z; \alpha) +G_{1}(x, y, z;\alpha) = (\frac{2048\alpha^7}{9\pi^3})^(\frac{1}{4})(z^2+x^2)e^(-\alpha r^2)$$
Corresponds to the $$3d_{z^2+x^2}$$ hydrogen atomic orbital.
This is a good tricky question because usually people would think that \[H_2\] only has two energy levels, but really there are more, just not occupied. Once you excite/add a good amount of energy, it could change to different orbitals.
( The math is right but Hydrogen has only five 3d orbitals and they are \(3d_{xy}\), \(3d_{xz}\), \(3d_{yz}\), \(3d_{y^2}\), and \(3d_{(x^2-y^2)}\) so the \(3d_{z^2+x^2}\) is not consistent . -RM)
Q11.27
Scientists are trying to theoretically predict the dipole moment of a CO molecule using the STO-3G and 6-31G* basis sets. When compared to their experimental data, the 6-31G* basis set provided a more accurate calculation than did the STO-3G basis set. Why is this?
S11.27
To calculate the dipole moment of a molecule, one needs an accurate description of the electron densities and molecular orbitals. This description becomes more accurate when a larger basis set is used, which is why the 6-31G* basis set gave more accurate calculations than did the STO-3G basis set.
Q11.28
The orbital energies calculated for formaldehyde using STO-3G an 3-21G basis sets are given below.
| Orbital | energy/Eh | energy/Eh |
|---|---|---|
| 1a1 | -20.3217 | -20.4856 |
| 2a1 | -11.1250 | -11.2866 |
| 3a1 | -1.3373 | -1.4117 |
| 4a1 | -0.8079 | -0.8661 |
| 1b2 | -0.6329 | -0.6924 |
| 5a1 | -0.5455 | -0.6345 |
| 1b1 | -0.4431 | -0.5234 |
| 2b2 | -0.3545 | -0.4330 |
| 2b1 | 0.2819 | 0.1486 |
| 6a1 | 0.6291 | 0.2718 |
| 3b2 | 0.7346 | 0.3653 |
| 7a1 | 0.9126 | 0.4512 |
Determine the ground-state electronic configuration of water. The photoelectron spectrum of water is shown below.
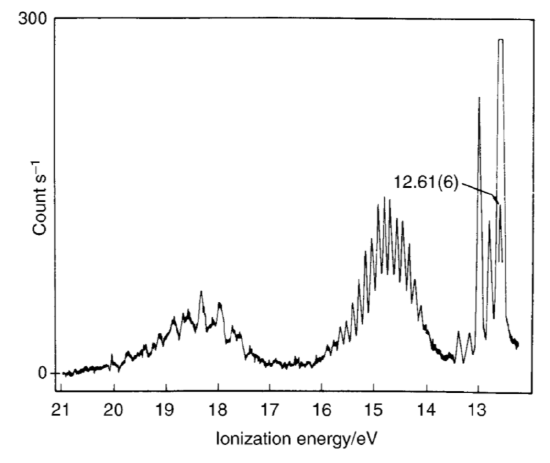
Assign the bands. Which calculated set of energies shows the best agreement with the photoelectron spectrum? Predict the ionization energy and electron affinity of water for each calculated set of energy levels. How do these compare with the experimental values?
S11.28
There are 8 electrons in water (2 from water and 6 from oxygen). This gives use the ground-state electronic configuration of
1a122a12 1b22 3a12 1b12
The band at approx. 15 eV corresponds to the 1b12 electrons, the bands at 15.5 eV correspond to 1b22 3a12 electrons. 18.5 ev = 1a122a12.
IE = -E2h2 = 0.6924*15 ev = 10.386 ev
EA = -E2h1 = 0.5234*18.5 ev = 9.6829 ev
Q11.29
The units of dipole moment given by Gaussian 94 are called debyes (D), after the Dutch-American chemist, Peter Debye, who was awarded the Nobel Prize for chemistry in 1936 for his work on dipole moments. One dehye is equal to 10-18 esu•cm where esu (electrostatic units) is a non-SI unit for electric charge. Given that a 9v battery is 3.0 x 10-2 esu, show that the conversion factor between debyes and C • m (coulomb • meters) is 1 D = 5.34 x 10^-38 C•m.
S11.29
\[1 D = 1*10^{-18} esu•cm\,\left( \frac{1.6022*10^{-19} \, C}{4.803*10^{-10}\, esu} *\dfrac{1 m}{100 cm} \right) = 3.3407*10^{-30} \, C•m\]
Q11.30
Determine the dipole moment SnCl2 by using the geometry and charges:
\[z= {e}\sum\, {X_i}{r_i}\]
S11.30
\[{e}((0.41sin(52.57)i+.041cos(52.75)j)94.7*10^{-12}m+(0.41sin(52.57)i+0.41cos(52.75)j)94.7x10^{-12}m)\]
\[{=2.3D}\]
Notes:
The equation I found for dipole moment is:
\[ \vec{\mu} = \sum_i q_i \, \vec{r}_i \]

