4.5: Eigenfunctions of Operators are Orthogonal
- Page ID
- 13410
- Understand the properties of a Hermitian operator and their associated eigenstates
- Recognize that all experimental obervables are obtained by Hermitian operators
Consideration of the quantum mechanical description of the particle-in-a-box exposed two important properties of quantum mechanical systems. We saw that the eigenfunctions of the Hamiltonian operator are orthogonal, and we also saw that the position and momentum of the particle could not be determined exactly. We now examine the generality of these insights by stating and proving some fundamental theorems. These theorems use the Hermitian property of quantum mechanical operators that correspond to observables, which is discuss first.
Hermitian Operators
Since the eigenvalues of a quantum mechanical operator correspond to measurable quantities, the eigenvalues must be real, and consequently a quantum mechanical operator must be Hermitian. To prove this, we start with the premises that \(ψ\) and \(φ\) are functions, \(\int d\tau\) represents integration over all coordinates, and the operator \(\hat {A}\) is Hermitian by definition if
\[ \int \psi ^* \hat {A} \psi \,d\tau = \int (\hat {A} ^* \psi ^* ) \psi \,d\tau \label {4-37} \]
This equation means that the complex conjugate of \(\hat {A}\) can operate on \(ψ^*\) to produce the same result after integration as \(\hat {A}\) operating on \(φ\), followed by integration. To prove that a quantum mechanical operator \(\hat {A}\) is Hermitian, consider the eigenvalue equation and its complex conjugate.
\[\hat {A} \psi = a \psi \label {4-38} \]
\[\hat {A}^* \psi ^* = a^* \psi ^* = a \psi ^* \label {4-39} \]
Note that \(a^* = a\) because the eigenvalue is real. Multiply Equation \(\ref{4-38}\) and \(\ref{4-39}\) from the left by \(ψ^*\) and \(ψ\), respectively, and integrate over the full range of all the coordinates. Note that \(ψ\) is normalized. The results are
\[ \int \psi ^* \hat {A} \psi \,d\tau = a \int \psi ^* \psi \,d\tau = a \label {4-40} \]
\[ \int \psi \hat {A}^* \psi ^* \,d \tau = a \int \psi \psi ^* \,d\tau = a \label {4-41} \]
Since both integrals equal \(a\), they must be equivalent.
\[ \int \psi ^* \hat {A} \psi \,d\tau = \int \psi \hat {A}^* \psi ^* \,d\tau \label {4-42} \]
The operator acting on the function,
\[\hat {A}^* \int \psi ^* \hat {A} \psi \,d\tau = \int \psi \hat {A} ^* \psi ^* \,d\tau_* \nonumber \]
produces a new function. Since functions commute, Equation \(\ref{4-42}\) can be rewritten as
\[ \int \psi ^* \hat {A} \psi d\tau = \int (\hat {A}^*\psi ^*) \psi d\tau \label{4-43} \]
This equality means that \(\hat {A}\) is Hermitian.
Eigenfunctions of a Hermitian operator are orthogonal if they have different eigenvalues.
Because of this theorem, we can identify orthogonal functions easily without having to integrate or conduct an analysis based on symmetry or other considerations.
\(ψ\) and \(φ\) are two eigenfunctions of the operator  with real eigenvalues \(a_1\) and \(a_2\), respectively. Since the eigenvalues are real, \(a_1^* = a_1\) and \(a_2^* = a_2\).
\[\hat {A} \psi = a_1 \psi \nonumber \]
\[\hat {A}^* \psi ^* = a_2 \psi ^* \nonumber \]
Multiply the first equation by \(φ^*\) and the second by \(ψ\) and integrate.
\[\int \psi ^* \hat {A} \psi \,d\tau = a_1 \int \psi ^* \psi \,d\tau \nonumber \]
\[\int \psi \hat {A}^* \psi ^* \,d\tau = a_2 \int \psi \psi ^* \,d\tau \label {4-45} \]
Subtract the two equations in Equation \ref{4-45} to obtain
\[\int \psi ^*\hat {A} \psi \,d\tau - \int \psi \hat {A} ^* \psi ^* \,d\tau = (a_1 - a_2) \int \psi ^* \psi \,d\tau \label {4-46} \]
The left-hand side of Equation \ref{4-46} is zero because \(\hat {A}\) is Hermitian yielding
\[ 0 = (a_1 - a_2 ) \int \psi ^* \psi \, d\tau \label {4-47} \]
If \(a_1\) and \(a_2\) in Equation \ref{4-47} are not equal, then the integral must be zero. This result proves that nondegenerate eigenfunctions of the same operator are orthogonal.
\(\square\)
Two wavefunctions, \(\psi_1(x)\) and \(\psi_2(x)\), are said to be orthogonal if
\[\int_{-\infty}^{\infty}\psi_1^\ast \psi_2 \,dx = 0. \label{4.5.1} \]
Consider two eigenstates of \(\hat{A}\), \(\psi_a(x)\) and \(\psi_{a'}(x)\), which correspond to the two different eigenvalues \(a\) and \(a'\), respectively. Thus,
\[A\psi_a = a \psi_a \label{4.5.2} \]
\[A\psi_a' = a' \psi_a' \label{4.5.3} \]
Multiplying the complex conjugate of the first equation by \(\psi_{a'}(x)\), and the second equation by \(\psi^*_{a'}(x)\), and then integrating over all \(x\), we obtain
\[ \int_{-\infty}^\infty (A \psi_a)^\ast \psi_{a'} dx = a \int_{-\infty}^\infty\psi_a^\ast \psi_{a'} dx, \label{ 4.5.4} \]
\[ \int_{-\infty}^\infty \psi_a^\ast (A \psi_{a'}) dx = a' \int_{-\infty}^{\infty}\psi_a^\ast \psi_{a'} dx. \label{4.5.5} \]
However, from Equation \(\ref{4-46}\), the left-hand sides of the above two equations are equal. Hence, we can write
\[(a-a') \int_{-\infty}^\infty\psi_a^\ast \psi_{a'} dx = 0. \nonumber \]
By assumption, \(a \neq a'\), yielding
\[\int_{-\infty}^\infty\psi_a^\ast \psi_{a'} dx = 0. \nonumber \]
In other words, eigenstates of an Hermitian operator corresponding to different eigenvalues are automatically orthogonal.
The eigenvalues of operators associated with experimental measurements are all real.
Draw graphs and use them to show that the particle-in-a-box wavefunctions for \(\psi(n = 2)\) and \(\psi(n = 3)\) are orthogonal to each other.
Solution
The two PIB wavefunctions are qualitatively similar when plotted
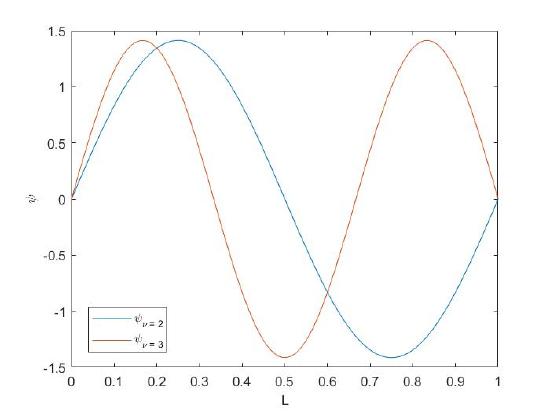
These wavefunctions are orthogonal when
\[\int_{-\infty}^{\infty} \psi(n=2) \psi(n=3) dx =0 \nonumber \]
and when the PIB wavefunctions are substituted this integral becomes
\[\begin{align*} \int_0^L \sqrt{\dfrac{2}{L}} \sin \left( \dfrac{2n}{L}x \right) \sqrt{\dfrac{2}{L}} \sin \left( \dfrac{2n}{L}x \right) dx &= ? \\[4pt] \dfrac{2}{L} \int_0^L \sin \left( \dfrac{2}{L}x \right) \sin \left( \dfrac{3}{L}x \right) &= ? \end{align*} \nonumber \]
We can expand the integrand using trigonometric identities to help solve the integral, but it is easier to take advantage of the symmetry of the integrand, specifically, the \(\psi(n=2)\) wavefunction is even (blue curves in above figure) and the \(\psi(n=3)\) is odd (purple curve). Their product (even times odd) is an odd function and the integral over an odd function is zero. Therefore \(\psi(n=2)\) and \(\psi(n=3)\) wavefunctions are orthogonal.
This can be repeated an infinite number of times to confirm the entire set of PIB wavefunctions are mutually orthogonal as the Orthogonality Theorem guarantees.
Orthogonality of Degenerate Eigenstates
Consider two eigenstates of \(\hat{A}\), \(\psi_a\) and \(\psi'_a\), which correspond to the same eigenvalue, \(a\). Such eigenstates are termed degenerate. The above proof of the orthogonality of different eigenstates fails for degenerate eigenstates. Note, however, that any linear combination of \(\psi_a\) and \(\psi'_a\) is also an eigenstate of \(\hat{A}\) corresponding to the eigenvalue \(a\). Thus, even if \(\psi_a\) and \(\psi'_a\) are not orthogonal, we can always choose two linear combinations of these eigenstates which are orthogonal. For instance, if \(\psi_a\) and \(\psi'_a\) are properly normalized, we can define the overlap integral
\[S= \int_{-\infty}^\infty \psi_a^\ast \psi_a' dx ,\label{ 4.5.10} \]
It is easily demonstrated (but not here) that
\[\psi_a'' = \frac{\vert S\vert}{\sqrt{1-\vert S\vert^2}}\left(\psi_a - S^{-1} \psi_a'\right) \label{4.5.11} \]
is a properly normalized eigenstate of \(\hat{A}\), corresponding to the eigenvalue \(a\), which is orthogonal to \(\psi_a\). It is straightforward to generalize the above argument to three or more degenerate eigenstates. Hence, we conclude that the eigenstates of a Hermitian operator are, or can be chosen to be, mutually orthogonal.
Degenerate eigenfunctions are not automatically orthogonal, but can be made so mathematically via the Gram-Schmidt Orthogonalization.
The above theorem argues that if the eigenvalues of two eigenfunctions are the same then the functions are said to be degenerate and linear combinations of the degenerate functions can be formed that will be orthogonal to each other. Since the two eigenfunctions have the same eigenvalues, the linear combination also will be an eigenfunction with the same eigenvalue. The proof of this theorem shows us one way to produce orthogonal degenerate functions.
If \(\psi_a\) and \(\psi'_a\) are degenerate, but not orthogonal, we can define a new composite wavefunction \(\psi_a'' = \psi'_a - S\psi_a\) where \(S\) is the overlap integral:
\[S= \langle \psi_a | \psi'_a \rangle \nonumber \]
then \(\psi_a\) and \(\psi_a'' \) will be orthogonal.
\[\begin{align*} \langle \psi_a | \psi_a'' \rangle &= \langle \psi_a | \psi'_a - S\psi_a \rangle \\[4pt] &= \cancelto{S}{\langle \psi_a | \psi'_a \rangle} - S \cancelto{1}{\langle \psi_a |\psi_a \rangle} \\[4pt] &= S - S =0 \end{align*} \nonumber \]
\(\square\)
Find \(N\) that normalizes \(\psi\) if \(\psi = N(φ_1 − Sφ_2)\) where \(φ_1\) and \(φ_2\) are normalized wavefunctions and \(S\) is their overlap integral.
\[S= \langle φ_1 | φ_2 \rangle \nonumber \]
- Answer
-
Remember that to normalize an arbitrary wavefunction, we find a constant \(N\) such that \(\langle \psi | \psi \rangle = 1\). This equates to the following procedure:
\[ \begin{align*} \langle\psi | \psi\rangle =\left\langle N\left(φ_{1} - Sφ_{2}\right) | N\left(φ_{1} - Sφ_{2}\right)\right\rangle &= 1 \\[4pt] N^2\left\langle \left(φ_{1} - Sφ_{2}\right) | \left(φ_{1}-Sφ_{2}\right)\right\rangle &=1 \\[4pt] N^2 \left[ \cancelto{1}{\langle φ_{1}|φ_{1}\rangle} - S \cancelto{S}{\langle φ_{2}|φ_{1}\rangle} - S \cancelto{S}{\langle φ_{1}|φ_{2}\rangle} + S^2 \cancelto{1}{\langle φ_{2}| φ_{2}\rangle} \right] &= 1 \\[4pt] N^2(1 - S^2 \cancel{-S^2} + \cancel{S^2})&=1 \\[4pt] N^2(1-S^2) &= 1 \end{align*} \nonumber \]
therefore
\[N = \dfrac{1}{\sqrt{1-S^2}} \nonumber \]
We conclude that the eigenstates of operators are, or can be chosen to be, mutually orthogonal.
Contributors and Attributions
Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)


\[ \int \psi'_a^* \psi_a d\tau \nonumber \]
then \(\psi_a\) and \(Φ\) will be orthogonal.
\[ \begin{align*} \int \psi_A^* Φ d\tau &= \int \psi_a^* (\psi'_a - S \psi_a ) d\tau \\[4pt] &= \int \psi_a^* \psi'_a d\tau - S \int \psi_a^*\psi_a d\tau \\[4pt] &= S - S = 0 \end{align*} \nonumber \]