25.3: Bose-Einstein Statistics and the Bose-Einstein Distribution Function
- Page ID
- 151987
For particles that follow Bose-Einstein statistics, we let the probability of a microstate of energy \(E\) in an \(N\)-particle system be \({\rho }^{BE}_{MS,N,E}\). For an isolated system of Bose-Einstein particles, the total probability sum is
\[1=\sum_{\{N_i\}}{W^{BE}\left(N_i,g_i\right){\rho }^{BE}_{MS,N,E}} \label{eq1} \]
We need to find \(W^{BE}\left(N_i,g_i\right)\), the number of ways to assign indistinguishable particles to the quantum states, if any number of particles can occupy the same quantum state.
We begin by considering the number of ways that \(N_i\) particles can be assigned to the \(g_i\) quantum states associated with the energy level \({\epsilon }_i\). We see that the fewest number of quantum states that can be used is one; we can put all of the particles into one quantum state. At the other extreme, we cannot use more than the \(N_i\) quantum states that we use when we give each particle its own quantum state. We can view this problem as finding the number of way we can draw as many as \(g_i\) boxes around \(N_i\) points. Let us create a scheme for drawing such boxes. Suppose we have a linear frame on which there is a row of locations. Each location can hold one particle. The frame is closed at both ends. Between each successive pair of particle-holding locations, there is a slot, into which a wall can be inserted. This frame is sketched in Figure 1.
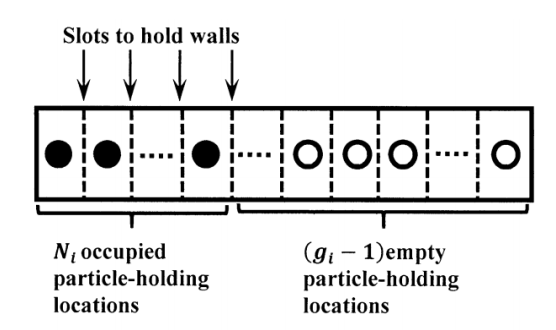
When we insert \(\left(g_i-1\right)\) walls into these slots, the frame contains \(g_i\) boxes. We want to be able to insert the walls so that the \(N_i\) particles are distributed among the \(g_i\) boxes in such a way that we can have any desired number of particles in any desired number of boxes. (Of course, placement of the walls is subject to the constraints that we use at most \(g_i\) boxes and exactly \(N_i\) particles.) We can achieve this by constructing the frame to have \(\left(N_i+g_i-1\right)\) particle-holding locations. To see this, we think about the case that requires the largest number of particle-holding locations. This is the case in which all \(N_i\) particles are in one box. (See Figure 2.) For this case, we need \(N_i\) occupied locations and \(\left(g_i-1\right)\) unoccupied locations.
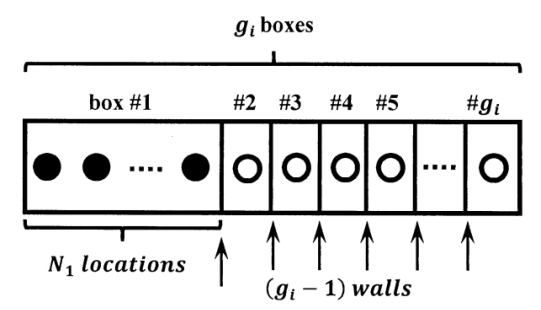
Now we consider the number of ways that we can insert \(\left(g_i-1\right)\) walls into the \(\left(N_i+g_i-1\right)\) slots. The first wall can go into any of \(\left(N_i+g_i-1\right)\) slots. The second can go into any of \(\left(N_i+g_i-1-\left(-1\right)\right)\) or \(\left(N_i+g_i-2\right)\) slots. The last wall can go into any of \(\left(N_i+g_i-1-\left(g_i-2\right)\right)\) or \(\left(N_i+1\right)\) slots. The total number of ways of inserting the \(\left(g_i-1\right)\) walls is therefore
\[\begin{align*} \left(N_i+g_i-1\right)\left(N_i+g_i-2\right)\dots \left(N_i+1\right) &=\frac{\left(N_i+g_i-1\right)\left(N_i+g_i-2\right)\dots \left(N_i+1\right)\left(N_i\right)\dots \left(2\right)\left(1\right)}{N_i!} \\[4pt] &=\frac{\left(N_i+g_i-1\right)!}{N_i!} \end{align*} \]
This total is greater than the answer we seek, because it includes all permutations of the walls. It does not matter whether the first, the second, or the last wall occupies a given slot. Therefore, the expression we have obtained over-counts the quantity we seek by the factor \(\left(g_i-1\right)!\), which is the number of ways of permuting the \(\left(g_i-1\right)\) walls. We have therefore that the \(N_i\) particles can be assigned to \(g_i\) quantum states in
\[\frac{\left(N_i+g_i-1\right)!}{N_i!\left(g_i-1\right)!} \nonumber \]
ways, and hence
\[ \begin{align*} W^{BE}\left(N_i,g_i\right) &=\left[\frac{\left(N_1+g_1-1\right)!}{\left(g_1-1\right)!N_1!}\right]\times \left[\frac{\left(N_2+g_2-1\right)!}{\left(g_2-1\right)!N_2!}\right]\times \dots \times \left[\frac{\left(N_i+g_i-1\right)!}{\left(g_i-1\right)!N_i!}\right]\times \dots \\[4pt] &=\prod^{\infty }_{i=1}{\left[\frac{\left(N_i+g_i-1\right)!}{\left(g_i-1\right)!N_i!}\right]} \end{align*} \]
so that the total probability sum for a Bose-Einstein system becomes (via Equation \ref{eq1}):
\[1=\sum_{\{N_j\}}{\prod^{\infty }_{i=1}{\left[\frac{\left(N_i+g_i-1\right)!}{\left(g_i-1\right)!N_i!}\right]}}{\left[{\rho }^{BE}\left({\epsilon }_i\right)\right]}^{N_i} \nonumber \]
To find the Bose-Einstein distribution function, we seek the population set \(\{N_1\mathrm{,\ }N_2\mathrm{,\dots ,\ }N_i\mathrm{,\dots }\}\) for which \(W^{BE}\) is a maximum, subject to the constraints
\[N=\sum^{\infty }_{i=1}{N_i} \nonumber \] and \[E=\sum^{\infty }_{i=1}{N_i}{\epsilon }_i \nonumber \]
The mnemonic function is
\[F^{BE}_{mn}=\sum^{\infty }_{i=1}{\left[\left(N_i+g_i-1\right){ \ln \left(N_i+g_i-1\right)-\left(N_i+g_i-1\right)\ }-N_i{ \ln N_1+N_i\ }-\left(g_i-1\right){ \ln \left(g_i-1\right)+\left(g_i-1\right)\ }\right]}+\alpha \left(N-\sum^{\infty }_{i=1}{N_i}\right)+\beta \left(E-\sum^{\infty }_{i=1}{N_i{\epsilon }_i}\right) \nonumber \]
We seek the \(N^{\textrm{⦁}}_i\) for which \(F^{BE}_{mn}\) is an extremum; that is, the \(N^{\textrm{⦁}}_i\) satisfying
\[\begin{align*} 0&=\frac{\partial F^{BE}_{mn}}{\partial N^{\textrm{⦁}}_i} \\[4pt] &=\frac{N^{\textrm{⦁}}_i+g_i-1}{N^{\textrm{⦁}}_i+g_i-1}+{ \ln \left(N^{\textrm{⦁}}_i+g_i-1\right)-1-\frac{N^{\textrm{⦁}}_i}{N^{\textrm{⦁}}_i}-{ \ln N^{\textrm{⦁}}_i\ }\ }+1-\alpha -\beta {\epsilon }_i \\[4pt]&=-{ \ln \frac{N^{\textrm{⦁}}_i}{N^{\textrm{⦁}}_i+g_i-1}\ }-\alpha -\beta {\epsilon }_i \end{align*} \]
Solving for \(N^{\textrm{⦁}}_i\), we find
\[N^{\textrm{⦁}}_i=\frac{\left(g_i-1\right)e^{-\alpha }e^{-\beta {\epsilon }_i}}{1-e^{-\alpha }e^{-\beta {\epsilon }_i}}\approx \frac{g_ie^{-\alpha }e^{-\beta {\epsilon }_i}}{1-e^{-\alpha }e^{-\beta {\epsilon }_i}} \nonumber \]
where the last expression takes advantage of the fact that \(g_i\) is usually a very large number, so the error introduced by replacing \(\left(g_i-1\right)\) by \(g_i\) is usually negligible. If \(1\gg e^{-\alpha }e^{-\beta {\epsilon }_i}\), the Bose-Einstein distribution function reduces to the Boltzmann distribution function. As we find in Section 25.2, this is always the case for a molecular gas at ambient temperatures.
Notes
\({}^{1}\)Richard C. Tolman, The Principles of Statistical Mechanics, Dover Publications, Inc., New York, 1979, pp 367-378. (This is a republication of the book originally published in 1938 by Oxford University Press.)
\({}^{2}\)Malcom Dole, Introduction to Statistical Thermodynamics, Prentice Hall, Inc., New York, 1954, pp 206-215.


