18.3: The Schrödinger Equation for A Particle in A Box

A problem usually called the particle in a box provides a convenient illustration of the principles involved in setting up and solving the Schrödinger equation. Besides being a good illustration, the problem also proves to be a useful approximation to many physical systems. The statement of the problem is simple. We have a particle of mass \(m\) that is constrained to move only in one dimension. For locations in the interval \(0\le x\le \ell\), the particle has zero potential energy. For locations outside this range, the particle has infinite potential energy. Since the particle cannot have infinite energy, this means that it can never find its way into locations outside of the interval \(0\le x\le \ell\). We can think of this particle as a bead moving on a wire, with stops located on the wire at \(x=0\) and at \(x=\ell\). We can also think of it as being confined to a one-dimensional box of length \(\ell\), which is the viewpoint represented by the name. The particle in a box model is diagrammed in Figure 1.

Figure 1. Potential energy versus distance for a particle in a box.

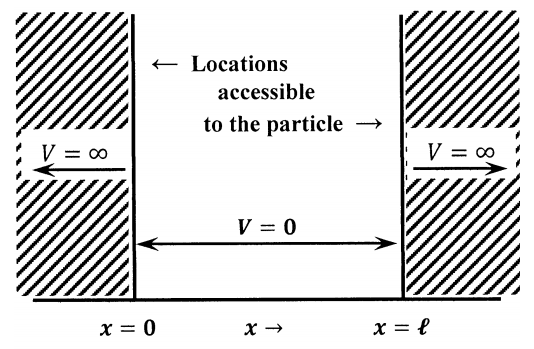
The potential energy constraints mean that the amplitude of the particle’s wavefunction must be zero, \(\psi \left(x\right)=0\), when the value of \(x\) lies in the interval

\[ - \infty x < 0 \nonumber \]

or

\[ \ell < x < + \infty \nonumber \]

We assume that the probability of finding the particle cannot change abruptly when its location changes by an arbitrarily small amount. This means that the wavefunction must be continuous, and it follows that \(\psi \left(0\right)=0\) and \(\psi \left(\ell \right)=0\). Inside the box, the particle’s Schrödinger equation is

\[-\left(\frac{h^2}{8{\pi }^2m}\right)\frac{d^2\psi }{dx^2}=E\psi \nonumber \]

and we seek those functions \(\psi \left(x\right)\) that satisfy both this differential equation and the constraint equations \(\psi \left(0\right)=0\) and \(\psi \left(\ell \right)=0\). It turns out that there are infinitely many such solutions, \({\psi }_n\), each of which corresponds to a unique energy level, \(E_n\).

To find these solutions, we first guess—guided by our considerations in §2—that solutions will be of the form \[\psi \left(x\right)=A{\mathrm{sin} \left(ax\right)\ }+B{\mathrm{cos} \left(bx\right)\ } \nonumber \]

A solution must satisfy

\[\psi \left(0\right)=A{\mathrm{sin} \left(0\right)\ }+B{\mathrm{cos} \left(0\right)\ }=B{\mathrm{cos} \left(0\right)=0\ } \nonumber \]

so that \(B=0\). At the other end of the box, we must have

\[\psi \left(\ell \right)=A{\mathrm{sin} \left(a\ell \right)\ }=0 \nonumber \]

which means that \(a\ell =n\pi\), where \(n\) is any integer: \(n\ =1,\ 2,\ \dots .\) Hence, we have

\[a={n\pi }/{\ell } \nonumber \]

and the only equations of the proposed form that satisfy the conditions at the ends of the box are

\[{\psi }_n\left(x\right)=A{\mathrm{sin} \left({n\pi x}/{\ell }\right)\ } \nonumber \]

To test whether these equations satisfy the Schrödinger equation, we check

\[-\left(\frac{h^2}{8{\pi }^2m}\right)\frac{d^2}{dx^2}\left[A{\mathrm{sin} \left(\frac{n\pi x}{\ell }\right)\ }\right]=E_n{\psi }_n \nonumber \]

and find

\[\left(\frac{h^2}{8{\pi }^2m}\right){\left(\frac{n\pi }{\ell }\right)}^2\left[A{\mathrm{sin} \left(\frac{n\pi x}{\ell }\right)\ }\right]=\left(\frac{n^2h^2}{8{m\ell }^2}\right){\psi }_n=E_n{\psi }_n \nonumber \]

so that the wavefunctions \({\psi }_n\left(x\right)=A{\mathrm{sin} \left({n\pi x}/{\ell }\right)\ }\) are indeed solutions and the energy, \(E_n\), associated with the wavefunction \({\psi }_n\left(x\right)\) is

\[E_n=\frac{n^2h^2}{8{m\ell }^2} \nonumber \]

We see that the energy values are quantized; although there are infinitely many energy levels, \(E_n\), only very particular real numbers—those given by the equation above—correspond to energies that the particle can have. If we sketch the first few wavefunctions, \({\psi }_n\left(x\right)\), we see that there are always \(n-1\) locations inside the box at which \({\psi }_n\left(x\right)\) is zero. These locations are called nodes. Once we know \(n\), we know the number of nodes, and we can sketch the general shape of the corresponding wavefunction. The first three wavefunctions and their squares are sketched in Figure 2.

Figure 2. Wave functions for a particle in a box.

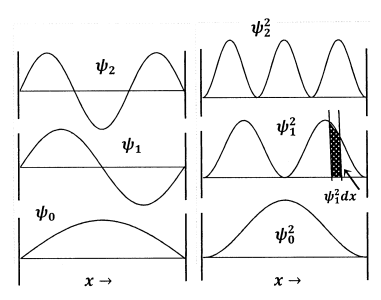
At this point, we have found a complete set of infinitely many solutions, except for the parameter \(A\). To determine \(A\), we interpret \({\psi }^2\left(x\right)\) as a probability density function, and we require that the probability of finding the particle in the box be equal to unity. This means that

\[1=\int^{\ell }_0{A^2{{\mathrm{sin}}^2 \left(\frac{n\pi x}{\ell }\right)\ }dx}=A^2\int^{\ell }_0{\left[\frac{1}{2}-\frac{1}{2}{\mathrm{cos} \left(\frac{2n\pi x}{\ell }\right)\ }\right]dx}=A^2\left(\frac{\ell }{2}\right) \nonumber \]

so that \(A=\sqrt{2/\ell }\), and the final wavefunctions are

\[{\psi }_n\left(x\right)=\sqrt{\frac{2}{\ell }}{\mathrm{sin} \left(\frac{n\pi x}{\ell }\right)\ } \nonumber \]