17.8: Electrolysis and the Faraday

Electrolytic cells are very important in the manufacture of products essential to our technology-intensive civilization. Only electrolytic processes can produce many materials, notably metals that are strong reducing agents. Aluminum and the alkali metals are conspicuous examples. Many manufacturing processes that are not themselves electrolytic utilize materials that are produced in electrolytic cells. These processes would not be possible if the electrolytic products were not available. For example, elemental silicon, the essential precursor of most contemporary computer chips, is produced from silicon tetrachloride by reduction with sodium.

\[SiCl_4+4\ Na^0\to Si^0+4\ NaCl \nonumber \]

(The silicon so produced is intensively refined, formed into large single crystals, and sliced into wafers before the chip-manufacturing process begins.) Elemental sodium is produced by the electrolysis of molten sodium chloride.

Successful electrolytic processes involve artful selection of the current-collector material and the reaction conditions. The design of the cell is often crucial. Since sodium metal reacts violently with water, we recognize immediately that electrolysis of aqueous sodium chloride solutions cannot produce sodium metal. What products are obtained depends on numerous factors, notably the composition of the electrodes, the concentration of the salt solution, and the potential that is applied to the cell.

Electrolysis of concentrated, aqueous, sodium chloride solutions is used on a vast scale in the chlor-alkali process for the co-production of chlorine and sodium hydroxide, both of which are essential for the manufacture of many common products.

\[2\ NaCl\left(aq\right)+2\ H_2O\left(\ell \right)\to 2\ NaOH\left(aq\right)+Cl_2\left(g\right)+H_2\left(g\right) \nonumber \]

Hydrogen is a by-product. The overall process does not involve sodium ion; rather, the overall reaction is an oxidation of chloride ion and a reduction of water.

\[2\ Cl^-\left(aq\right)\to Cl_2\left(g\right)+2\ e^- \nonumber \] oxidation half-reaction \[2\ H_2O\left(\ell \right)+2\ e^-\to 2\ OH^-\left(aq\right)+H_2\left(g\right) \nonumber \]

reduction half-reaction

The engineering difficulties associated with the chlor-alkali process are substantial. They occur because hydroxide ion reacts with chlorine gas; a practical cell must be designed to keep these two products separate. Commercially, two different designs have been successful. The diaphragm-cell process uses a porous barrier to separate the anodic and cathodic cell compartments. The mercury-cell process uses elemental mercury as the cathodic current collector; in this case, sodium ion is reduced, but the product is sodium amalgam (sodium–mercury alloy) not elemental sodium. Like metallic sodium, sodium amalgam reduces water, but the amalgam reaction is much slower. The amalgam is removed from the cell and reacted with water to produce sodium hydroxide and regenerate mercury for recycle to the electrolytic cell.

Elemental sodium is manufactured by the electrolysis of molten sodium chloride. This is effected commercially using an iron cathode and a carbon anode. The reaction is

\[NaCl\left(\ell \right)\to {Na}^0+Cl_2\left(g\right) \nonumber \]

Figure 6. An electrolytic cell for the production of sodium metal.

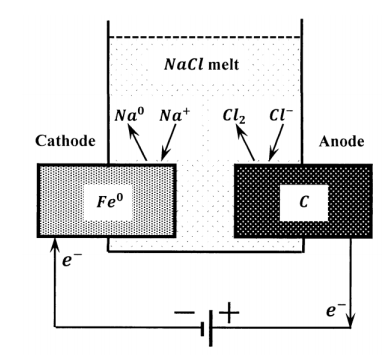
Such a cell is diagrammed in Figure 6. A mechanical barrier suffices to keep the products separate and prevent their spontaneous reaction back to the salt. A more significant problem in the design of the cell was to find an anode material that did not react with the chlorine produced. From the cell reaction, we see that one electron passes through the external circuit for every sodium atom that is produced. The charge that passes through the external circuit during the production of one mole of sodium metal is, therefore, the charge on one mole of electrons.

In honor of Michael Faraday, the magnitude of the charge carried by a mole of electrons is called the faraday. The faraday constant is denoted by the symbol “\(\mathcal{F}\).” That is,

\[1\mathcal{F}=\frac{6.02214\times {10}^{23}\mathrm{\ electrons}}{\mathrm{mol}}\times \frac{1.602187\times {10}^{-19}\ C}{\mathrm{electron}}=96,485\ C\ {\mathrm{mol}}^{-1} \nonumber \]

The faraday is a useful unit in electrochemical calculations. The unit of electrical current, the ampere, is defined as the passage of one coulomb per second. Knowing the current in a circuit and the time for which it is passed, we can calculate the number of coulombs that are passed. Remembering the value of one faraday enables us to do stoichiometric calculations without bringing in Avogadro’s number and the electron charge every time.

Tabulated information about the thermodynamic characteristics of half-reactions enable us to make useful predictions about what can and cannot occur in various cells that we might think of building. This information can be used to predict the potential difference that will be observed in a galvanic cell made by connecting two arbitrarily selected half-cells. In any electrolytic cell, more than one electron-transfer reaction can usually occur. In the chlor-alkali process, for example, water rather than chloride ion might be oxidized at the anode. In such cases, tabulated half-cell data enable us to predict which species can react at a particular applied potential.