12.7: Phase Equilibria - Temperature Dependence of the Melting Point

We can also represent reversible changes by paths on contour maps. In Figure 5, a Gibbs free energy surface is represented as a contour map.

Figure 5. The path of a changing system depicted on a map of constant Gibbs free energy contours.

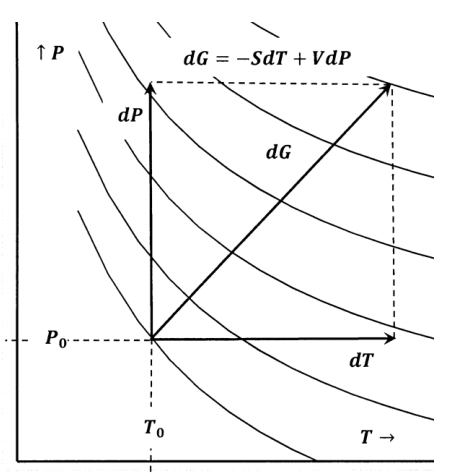
For small changes in \(T\) and \(P\), we can evaluate

\[dG=G\left(P_0+dP,T_0+dT\right)-G\left(P_0,T_0\right) \nonumber \]

from

\[dG=-S\left(P_0,T_0\right)dT+V\left(P_0,T_0\right)dP \nonumber \]

For larger changes, we can integrate along the paths \(P=P_0\) and \(T=T_0+\Delta T\) to find

\[\Delta G=\int^{T_0+\Delta T}_{T_0}{-S\left(P_0,T\right)dT+}\int^{P_0+\Delta P}_{P_0}{V\left(P,T_0+\Delta T\right)dP} \nonumber \]

The calculation of \(\Delta S\) in Section 12.5 could be similarly represented as a path in the temperature–pressure plane that connects two constant-entropy contours.

Analysis of solid–liquid equilibrium parallels that of liquid–vapor equilibrium. Let us again consider the equilibrium between ice and water. Given that ice and water are at equilibrium at a particular temperature and pressure, and supposing that we increase the pressure from this equilibrium value, how must the temperature change in order that the system remain at equilibrium? In Section 6.6, we use Le Chatelier’s principle to answer this question qualitatively. Now, we find a quantitative answer by an argument that closely parallels that in Section 12.7.

Figure 6. Gibbs free energy changes in a cycle connecting two solid-liquid equilibrium states.

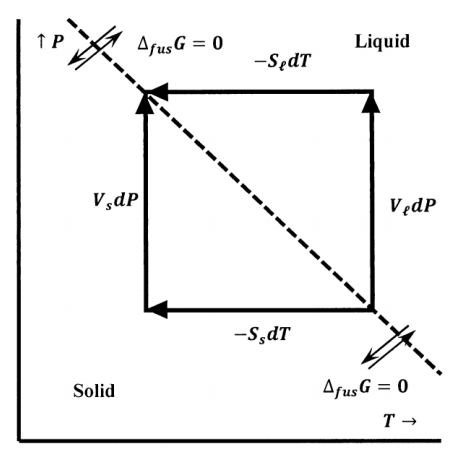
Figure 6 depicts the line of pressures and temperatures along which ice and water are in equilibrium. We can view this as a contour map. In this case, the contours are sets of pressures and temperatures for which \({\Delta }_{fus}\overline{G}\) is constant. Only the contour for \({\Delta }_{fus}\overline{G}=0\) is shown. The figure also depicts paths along which ice and water can individually be taken from their equilibrium state at \(P\) and \(T\) to their equilibrium state at \(P+dP\) and \(T+dT\). The Gibbs free energy change for the ice must equal that for water. Letting \({\overline{G}}_{\ell }\), \({\overline{S}}_{\ell }\), and \({\overline{V}}_{\ell }\) be the Gibbs free energy, the entropy, and the volume of one mole of water at temperature \(T\) and pressure \(P\), the equation

\[d{\overline{G}}_{\ell }={\overline{V}}_{\ell }dP-{\overline{S}}_{\ell }dT \nonumber \]

specifies the change in the Gibbs free energy of one mole of water when the pressure changes \(P\) to \(P+dP\) and the temperature changes from \(T\) to \(T+dT\). Similarly, using the subscript “s” to denote ice, we have

\[d{\overline{G}}_s={\overline{V}}_sdP-{\overline{S}}_sdT \nonumber \]

Since these Gibbs free energy changes connect states of ice–water equilibrium, they must be equal, and we have

\[d{\overline{G}}_{\ell }-d{\overline{G}}_s=\left({\overline{V}}_{\ell }-{\overline{V}}_s\right)dP-\left({\overline{S}}_{\ell }-{\overline{S}}_s\right)dT={\Delta }_{fus}\overline{V}dP-{\Delta }_{fus}\overline{S}dT=0 \nonumber \]

where we introduce \({\Delta }_{fus}\overline{S}\) and \({\Delta }_{fus}\overline{V}\) to represent the entropy and volume changes that occur when one mole of ice melts reversibly at \(P\) and \(T\). Rearranging gives

\[\frac{dP}{dT}=\frac{\Delta_{fus}\overline{S}}{\Delta_{fus}\overline{V}} \nonumber \]

Since

\[\Delta_{fus}\overline{S}={\Delta_{fus}\overline{H}}/{T}, \nonumber \]

the Clapeyron equation becomes

\[\frac{dP}{dT}=\frac{\Delta_{fus}\overline{H}}{T\ {\Delta }_{fus}\overline{V}} \nonumber \]

At a pressure of one bar and a temperature of 273.15 K, the enthalpy of fusion is \(\mathrm{6010}\ \mathrm{J}\ {\mathrm{mol}}^{\mathrm{-1}}\ {\mathrm{K}}^{-1}\). The enthalpy value changes only slowly as the equilibrium temperature changes. The volumes of one mole of ice and one mole of water are 19.651 and 18.019 \({\mathrm{cm}}^3\), respectively. At 273.15 K, we obtain

\[\frac{dP}{dT}=-143.7\ \mathrm{bar}\ {\mathrm{K}}^{-1} \nonumber \]

If the pressure increases to 1000 bar, the change in the melting point is about –6.96 K, so that \(T_{mp}\left(1000\ \mathrm{bar}\right)=266.2\ \mathrm{K}\).

Again, this analysis is successful because the constituents are pure phases; the properties of the ice are independent of how much water is present and vice versa. When we analyze the equilibrium between ice and salt water, the properties of the salt water depend on the kind of salt present and on its concentration.