9.7: Entropy Changes for A Spontaneous Process in An Isolated System
- Page ID
- 152082
In Section 9.6, we consider the entropy changes in a system and its surroundings when the process is reversible. We consider now the diametrically opposite situation in which an isolated system undergoes a spontaneous change. From the entropy-based statement of the second law, we know how the entropy of this system and its surroundings change. Since the system is isolated, no change occurs in the surroundings. Thus, \(\Delta \hat{S}=0\); and since \(\Delta S+\Delta \hat{S}>0\), we have \(\Delta S>0\).
Let us attempt to develop these conclusions from the machine-based statement of the second law. Since the process occurs irreversibly, we cannot use the heat of the process to find the entropy change for the system. We can calculate the entropy change for a process from the defining equation only if the process is reversible. However, entropy is a state function; using the figure of speech that we introduce in Section 7.21, we can find the entropy change for the spontaneous process by evaluating \(\Delta S\) along a second and reversible path that connects the same initial and final states.
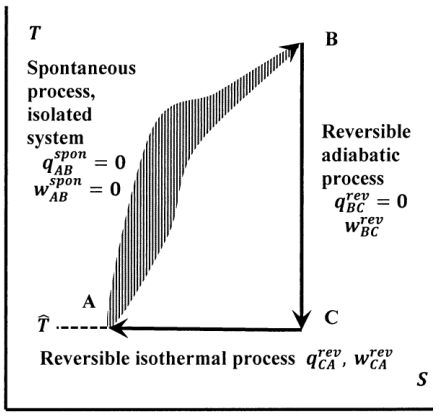
In Figure 7, these paths are diagrammed in temperature–entropy space. The transition from state A to state B occurs irreversibly, and therefore it does not necessarily correspond to a path that we can specify on this diagram. The dashed line drawn for this transition is supposed to remind us of this fact. We can readily devise a reversible path from B back to A. First, we reversibly and adiabatically return the temperature of the system to its original value \(\hat{T}\). In this step, the system does work on the surroundings, or vice versa. The system reaches point C on the diagram. Then we reversibly and isothermally add or remove heat from the system to return to the original state at point A. For the transfer of heat to be reversible, we must have \(T=\hat{T}\) for this step. Hence, the final (and original) temperature of the system at point A is equal to the temperature of the surroundings. The reversible path \(B\to C\to A\) must exist, because the tiling theorem asserts that adiabats (vertical lines) and isotherms (horizontal lines) tile the \(T--S\)-plane arbitrarily densely.
Taken literally, this description of state A is inconsistent. We suppose that the initial state A is capable of spontaneous change; therefore, it cannot be an equilibrium state. We suppose that the final state A is reached by a reversible process; therefore, it must be an equilibrium state. We bridge this contradiction by refining our definition of the initial state. The final state A is an equilibrium state with well-defined state functions. What we have in mind is that these final equilibrium-state values also characterize the initial non-equilibrium state. Evidently, the initial state A that we have in mind is a hypothetical state. This hypothetical state approximates the state of a real system that undergoes spontaneous change. By invoking this hypothetical initial state, we eliminate the contradiction between our descriptions of initial state A and final state A. Given a real system that undergoes spontaneous change, we must find approximate values for the real system’s state functions by finding an equilibrium—or quasi-equilibrium—system that adequately models the initial state of the spontaneously changing system.
In the development below, we place no constraints on the nature of the system or the spontaneous process. We assume that the state functions of any hypothetical initial state A can be adequately approximated by some equilibrium-state model. However, before we consider the general argument, let us show how these conditions can be met for another specific system. Consider a vessel whose interior is divided by a partition. The real gas of a pure substance occupies the space on one side of the partition. The space on the other side of the partition is evacuated. We suppose that this vessel is isolated. The real gas is at equilibrium. We can measure its state functions, including its pressure, volume, and temperature. Now suppose that we puncture the partition. As soon as we do so, the gas expands spontaneously to fill the entire vessel, reaching a new equilibrium position, at a new pressure, volume, and temperature. The gas undergoes a free expansion, as defined in Section 7.17.
At the instant the partition is punctured, the system becomes able to undergo spontaneous change. In this hypothetical initial state, before any significant quantity of gas passes through the opening, neither the actual condition of the gas nor the values of its state functions have changed. After the expansion to the new equilibrium state, the original state can be restored by reversible processes of adiabatic compression and isothermal volume adjustment. (Problems 13 and 14 in Chapter 10 deal with the energy and entropy changes for ideal and real gases around a cycle in which spontaneous expansion in an isolated system is followed by reversible restoration of the initial state.)
Returning to the general cycle depicted in Figure 7, we see that there are some important conditions on the heat and work terms in the individual steps. Since the system is isolated while it undergoes the transition from A to B, it exchanges no heat or work with the surroundings in this step: \(q^{spon}_{AB}=w^{spon}_{AB}=0\). For the reversible adiabatic transition from B to C, \(d_{BC}q^{rev}=0\) in every incremental part of the path. The transition from C to A occurs reversibly and isothermally; letting the heat of this step be \(q^{rev}_{CA}\), the entropy changes for these reversible steps are, from the defining equation,
\[{\Delta }_{BC}S=\int^{T_C}_{T_B}{\frac{d_{BC}q^{rev}}{T}}=0 \nonumber \] and \[{\Delta }_{CA}S=\frac{q^{rev}_{CA}}{\hat{T}} \nonumber \]
The energy and entropy changes around this cycle must be zero, whether the individual steps occur reversibly or irreversibly. We have
\[\Delta E=q^{spon}_{AB}+w^{spon}_{AB}+q^{rev}_{BC}+w^{rev}_{BC}+q^{rev}_{CA}+w^{rev}_{CA}=q^{rev}_{CA}+w^{rev}_{BC}+w^{rev}_{CA}=0 \nonumber \] and
\[\Delta S={\Delta }_{AB}S+{\Delta }_{BC}S+{\Delta }_{CA}S ={\Delta }_{AB}S+{q^{rev}_{CA}}/{\hat{T}}=0 \nonumber \]
We want to analyze this cycle using the machine-based statement of the second law. We have \(w^{rev}_{BC}=-{\hat{w}}^{rev}_{BC}\), \(w^{rev}_{CA}=-{\hat{w}}^{rev}_{CA}\), and \(q^{rev}_{CA}=-{\hat{q}}^{rev}_{CA}\). Let us assume that the system does net work on the surroundings as this cycle is traversed so that \({\hat{w}}^{rev}_{BC}+{\hat{w}}^{rev}_{CA}>0\). Then,
\[-\left({\hat{w}}^{rev}_{BC}+{\hat{w}}^{rev}_{CA}\right)=w^{rev}_{BC}+w^{rev}_{CA}<0 \nonumber \]
and it follows that \(q^{rev}_{CA}>0\). The system exchanges heat with the surroundings in only one step of this process. In this step, the system extracts a quantity of heat from a reservoir in the surroundings. The temperature of this reservoir remains constant at \(\hat{T}\) throughout the process. The heat extracted by the system is converted entirely into work. This result contradicts the machine-based statement of the second law. Hence, \(w^{rev}_{BC}+w^{rev}_{CA}<0\) is false; it follows that
\[w^{rev}_{BC}+w^{rev}_{CA}\ge 0 \nonumber \]
and that \[q^{rev}_{CA}\le 0 \nonumber \]
For the entropy change in the spontaneous process in the isolated system, we have
\[{\Delta }_{AB}S=-{q^{rev}_{CA}}/{\hat{T}}\ge 0 \nonumber \]
Now, we introduce the premise that \(q^{rev}_{CA}\neq 0\). If this is true, the entropy change in the spontaneous process in the isolated system becomes
\[{\Delta }_{AB}S>0 \nonumber \]
(The converse is also true; that is, \({\Delta }_{AB}S>0\) implies that \(q^{rev}_{CA}\neq 0\).) The premise that \(q^{rev}_{CA}\neq 0\) is independent of the machine-based statement of the second law, which requires only that \(q^{rev}_{CA}\le 0\), as we just demonstrated. It is also independent of the first law, which requires only that \(q^{rev}_{CA}=-w^{rev}_{BC}-w^{rev}_{CA}\). If \(q^{rev}_{CA}\neq 0\), we can conclude that, for a spontaneous process in an isolated system, we must have \(w_{BC}+w_{CA}>0\) and \(q^{rev}_{CA}<0\). These conditions correspond to doing work on the system and finding that heat is liberated by the system. There is no objection to this; it is possible to convert mechanical energy into heat quantitatively. The conclusions that \(q^{rev}_{CA}<0\) and \({\Delta }_{AB}S>0\) have important consequences; we consider them below. First, however, we consider a line of thought that leads us to infer that \(q^{rev}_{CA}\neq 0\) and hence that \(q^{rev}_{CA}<0\) must be true.
Because \(q_{AB}=0\) and \(w_{AB}=0\), we have \({\ E}_A=E_B\). The system can be taken from state A to state B by the reversible process A\(\to C\to B\). Above we see that if \(q^{rev}_{CA}=0\), we have \({\ S}_A=S_B\). In §6-10, we introduce Duhem’s theorem, which asserts that two thermodynamic variables are sufficient to specify the state of a closed reversible system in which only pressure–volume work is possible. We gave a proof of Duhem’s theorem when the two variables are chosen from among the pressure, temperature, and composition variables that describe the system. We avoided specifying whether other pairs of variables can be used. If we assume now that specifying the variables energy and entropy is always sufficient to specify the state of such a system, it follows that states A and B must in fact be the same state. (In §14, and in greater detail in Chapter 10, we see that the first law and our entropy-based statement of the second law do indeed imply that specifying the energy and entropy specifies the state of a closed reversible system in which only pressure–volume work is possible.)
If state A and state B are the same state; that is, if the state functions of state A are the same as those of state B, it is meaningless to say that there is a spontaneous process that converts state A to state B. Therefore, if A can be converted to B in a spontaneous process in an isolated system, it must be that \(q^{rev}_{CA}\neq 0\). That is,
\[\left[\left(q^{rev}_{CA}=0\right)\Rightarrow \sim \left(\mathrm{A\ can\ go\ to\ B\ spontaneously}\right)\right] \nonumber \] \[\Rightarrow \left[\left(A\ \mathrm{can\ go\ to\ B\ spontaneously}\right)\Rightarrow \left(q^{rev}_{CA}\neq 0\right)\right] \nonumber \]
From the machine-based statement of the second law, we find \({\Delta }_{AB}S=-{q^{rev}_{CA}}/{\hat{T}}\ge 0\). When we supplement this conclusion with our Duhem’s theorem-based inference that \(q^{rev}_{CA}\neq 0\), we can conclude that \(\Delta S>0\) for any spontaneous process in any isolated system. Because the system is isolated, we have \(\hat{q}=0\), and \(\Delta \hat{S}=0\). For any spontaneous process in any isolated system we have
\[\Delta S_{universe}=\Delta S+\Delta \hat{S}>0. \nonumber \]
We can also conclude that the converse is true; that is, if \({\Delta }_{AB}S=S_B-S_A>0\) for a process in which an isolated system goes from state A to state B, the process must be spontaneous. Since any process that occurs in an isolated system must be a spontaneous process, it is only necessary to show that \({\Delta }_{AB}S>0\) implies that state B is different from state A. This is trivial. Because entropy is a state function, \(S_B-S_A>0\) requires that state B be different from state A.
None of our arguments depends on the magnitude of the change that occurs. Evidently, the same inequality must describe every incremental portion of any spontaneous process; otherwise, we could define an incremental spontaneous change for which the machine-based statement of the second law would be violated. For every incremental part of any spontaneous change in any isolated system we have \(dS>0\) and
\[dS_{universe}=dS+d\hat{S}>0. \nonumber \]
These are pivotally important results; we explore their ramifications below. Before doing so, however, let us again consider a system in which only pressure–volume work is possible. There is an alternative way to express the idea that such a system is isolated. Since an isolated system cannot interact with its surroundings in any way, it cannot exchange energy with its surroundings. Its energy must be constant. Since it cannot exchange pressure–volume work, its volume must be constant. Hence, isolation implies constant \(E\) and \(V\). If only pressure–volume work is possible, the converse must be true; that is, if only pressure–volume work is possible, constant energy and volume imply that there are no interactions between the system and its surroundings. Therefore, constant \(E\) and \(V\) imply that the system is isolated, and it must be true that \(\Delta \hat{S}=0\). In this case, a spontaneous process in which \(E\) and \(V\) are constant must be accompanied by an increase in the entropy of the system. (If \(V\) is constant and only pressure–volume work is possible, the process involves no work.) We have a criterion for spontaneous change:
\[{\left(\Delta S\right)}_{EV}>0 \nonumber \] (spontaneous process, only pressure–volume work)
where the subscripts indicate that the energy and volume of the system are constant. (In Section 9.21, we arrive at this conclusion by a different argument.)


