9.3: The Carnot Cycle for Any Reversible System

To show that \(\oint dq^{rev}/T=0\) for any reversible system taken around a Carnot cycle, we first observe that the Carnot cycle can be traversed in the opposite direction. In this case, work is delivered to the engine and a quantity of heat is transferred from the low-temperature reservoir to the high-temperature reservoir. Operated in reverse, the Carnot engine is a refrigerator. Suppose that we have two identical ideal-gas Carnot machines, one of which we operate as an engine while we operate the other as a refrigerator. If we configure them so that the work output of the engine drives the refrigerator, the effects of operating them together cancel completely. The refrigerator exactly consumes the work output of the engine. The heat transfers to and from the heat reservoirs offset exactly.

Now, let us consider an ideal-gas Carnot engine and any other reversible engine that extracts heat from a high-temperature reservoir and rejects a portion of it to a low-temperature reservoir. Let us call these engines A and B. We suppose that one is operated to produce work in its surroundings (\(w<0\)); the other is operated to consume this work and transfer net heat energy from the low-temperature to the high-temperature reservoir. Let the net work done in one cycle on machines A and B be \(w_{netA}\) and \(w_{netB}\), respectively. We can choose to make these engines any size that we please. Let us size them so that one complete cycle of either engine exchanges the same quantity of heat with the high-temperature reservoir. That is, if the high-temperature reservoir delivers heat \(q_{hA}\) to engine A, then it delivers heat \(q_{hB}=q_{hA}\) to engine B. Figure 3 diagrams these engines. With one operating as an engine and the other operating as a refrigerator, we have \(q_{hA}+q_{hB}=0\). When both engine and refrigerator have completed a cycle, the high temperature reservoir has returned to its original state.

Figure 3. Matched heat engine and refrigerator and a system that combines them.

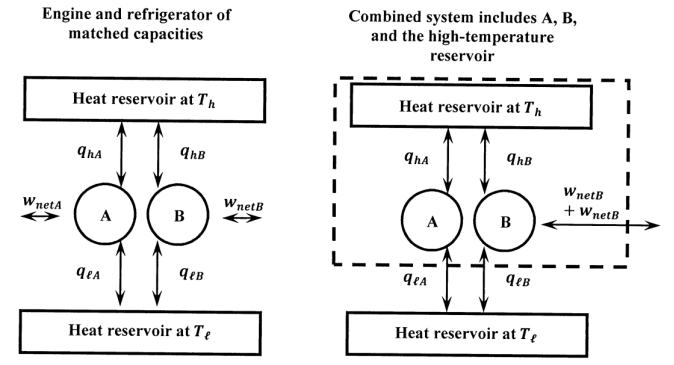
We can create a combined device that consists of A running as an engine, B running as a refrigerator, and the high-temperature reservoir. Figure 3 also diagrams this combination. When it executes one complete cycle, the initial condition of the combined device is restored. Therefore, since E is a state function, we have

\[\begin{align} \Delta E &= w_{netA}+q_{hA}+q_{\ell A}+w_{netB}+q_{hB}+q_{\ell B} \\[4pt] &=w_{netA}+w_{netB}+q_{\ell A}+q_{\ell B} \\[4pt] &=0. \end{align} \nonumber \]

where we use the constraint \(q_{hA}+q_{hB}=0\). Let us consider the possibility that \(w_{netA}+w_{netB}<0\); that is, the combined device does net work on the surroundings. Then, \(\Delta E=0\) implies that \(q_{\ell A}+q_{\ell B}>0\).

In this cyclic process, the combined device takes up a positive quantity of heat from a constant-temperature reservoir and delivers a positive quantity of work to the surroundings. There is no other change in either the system or the surroundings. This violates the machine-based statement of the second law. Evidently, it is not possible for the combined device to operate in the manner we have hypothesized. We conclude that any such machine must always operate such that \(w_{netA}+w_{netB}\ge 0\); that is, the net work done on the combined machine during any complete cycle must be either zero or some positive quantity.

In concluding that \(w_{netA}+w_{netB}\ge 0\), we specify that the combined machine has A running as a heat engine and B running as a refrigerator. Now, suppose that we reverse their roles, and let \(w^*_{netA}\) and \(w^*_{netB}\) represent the net work for the reversed combination. Applying the same argument as previously, we conclude that \(w^*_{netA}+w^*_{netB}\ge 0\). But, since the direction of operation is reversed for both machines, we must also have \(w^*_{netA}=-w_{netA}\) and \(w^*_{netB}=-w_{netB}\). Hence we have \(-w_{netA}-w_{netB}\ge 0\) or \(w_{netA}+w_{netB}\le 0\). We conclude, therefore, that

\[w_{netA}+w_{netB}=0 \nonumber \]

for any two, matched, reversible engines operating around a Carnot cycle.

This conclusion can be restated as a condition on the efficiencies of the two machines. The individual efficiencies are \({\epsilon }_A=-w_{netA}/q_{hA}\) and \({\epsilon }_B=-w_{netB}/q_{hB}\).

(The efficiency equation is unaffected by the direction of operation, because changing the direction changes the sign of every energy term in the cycle. Changing the direction of operation is equivalent to multiplying both the numerator and denominator by minus one.) Then, from \(w_{netA}+w_{netB}=0\), it follows that

\[{\epsilon }_Aq_{hA}+{\epsilon }_Bq_{hB}=0 \nonumber \]

Since we sized A and B so that \(q_{hA}+q_{hB}=0\), we have

\[\epsilon_Aq_{hA}-{\epsilon }_Bq_{hA}=0 \nonumber \] so that \[{\epsilon }_A={\epsilon }_B \nonumber \]

for any reversible Carnot engines A and B operating between the same two heat reservoirs.

For the ideal gas engine, we found \(\epsilon =1-T_{\ell }/{T_h}\). For any reversible Carnot engine, we have \(\Delta E=0=w_{net}+q_h+q_{\ell }\), so that \(-w_{net}=q_h+q_{\ell }\), and

\[\epsilon =\frac{-w_{net}}{q_h}=1+\frac{q_{\ell }}{q_h} \nonumber \]

This means that the efficiency relationship

\[\epsilon =1-\frac{T_{\ell }}{T_h}=1+\frac{q_{\ell }}{q_h} \nonumber \]

applies to any reversible Carnot engine. It follows that the integral of \(dq^{rev}/T\) around a Carnot cycle is zero for any reversible system.

The validity of these conclusions is independent of type of work that the engine produces; if engine A is an ideal-gas engine, engine B can be comprised of any system and can produce any kind of work. In obtaining this result from the machine-based statement of the second law, we make the additional assumption that pressure–volume work can be converted entirely to any other form of work, and vice versa. That is, we assume that the work produced by engine A can reversibly drive engine B as a refrigerator, whether engines A and B produce the same or different kinds of work.