7.14: Heat Capacities of Solids- the Law of Dulong and Petit
- Page ID
- 152037
It is easy to maintain a constant pressure on a solid while varying its temperature. To keep its volume rigorously constant over a range of temperatures is difficult. Because the direct measurement of \(C_P\) is straightforward, most heat-capacity experiments on solids measure \(C_P\). In Section 10.9, we derive a general relationship between \(C_P\), \(C_V\), and other measurable properties of a substance. This relationship makes it possible to evaluate \(C_V\) indirectly. For a solid, this relationship shows that \(C_P\) and \(C_V\) are usually about the same.
Heat capacities of solids have been investigated over wide temperature ranges. For most solids, \(C_P\) is approximately constant at room temperature and above. For any of the heavier elements, this constant has about the same value. This observation was first made in 1819. It is called the law of Dulong and Petit, in honor of the discoverers. It played an important role in the establishment of correct atomic weights for the elements. The value of the constant found by Dulong and Petit is about \(3R\). Remarkably, the law can be extended to polyatomic molecules containing only the heavier elements. Often the solid-state heat capacity of such molecules is about \(\mathrm{3}R\) per mole of atoms in the molecule. Correlations that are more detailed have been developed. These relate the heat capacity of a mole of a molecular solid to its molecular formula. In such correlations, the heat capacity per mole increases by a fixed increment for each atom of, say, carbon in the molecule; by a different fixed increment for each atom of nitrogen in the molecule; etc. For the lighter elements, the increments are less than \(\mathrm{3}R\). For the heavier elements, the increment is approximately \(\mathrm{3}R\), as observed by Dulong and Petit.
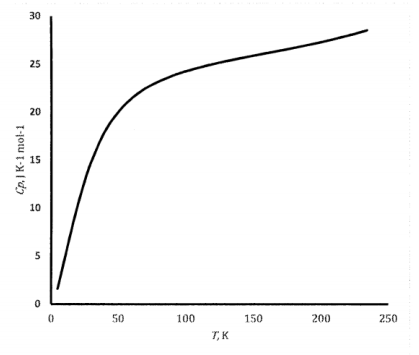
As the temperature of any solid decreases, its heat capacity eventually begins to decrease. At temperatures near absolute zero, the heat capacity approaches zero. The graph in Figure 6 shows the shape of the heat capacity versus temperature curve for solid mercury. The shape of this curve can be predicted from a very simple model for the energy modes available to the atoms in a solid. Albert Einstein developed this model in 1907. Einstein’s model for the heat capacity of a solid was an important milestone in the development of quantum mechanics. Since then, the basic ideas have been extended and refined to create more detailed theories that achieve good quantitative agreement with the experimental results for particular substances. We discuss Einstein’s treatment in Section 22.6.


