4.15: The Geometry of A Collision between Spherical Molecules
- Page ID
- 151998
Thus far we have not concerned ourselves with the relative orientation of a pair of colliding molecules. We want to develop a more detailed model for the collision process\({}^{1}\) itself, and the first step is to specify what we mean by relative orientation.
As before, we consider a molecule of type \(1\) moving with the relative velocity \(v_{12}\) through a gas of stationary type\(\ 2\) molecules. In unit time, molecule \(1\) travels a distance \(v_{12}\) and collides with many molecules of type \(2\). We can characterize each such collision by the angle, \(\theta\), between the velocity vector and the line of centers of the colliding pair. For glancing collisions, we have \(\theta ={\pi }/{2}\). For head-on collisions, we have \(\theta =0\). All else being equal, the collision will be more violent the smaller the angle \(\theta\). Evidently, we can describe the average effect of collisions more completely if we can specify the frequency of collisions as a function of \(\theta\). More precisely, we want to find the frequency of collisions in which this angle lies between \(\theta\) and \(\theta +d\theta\).
When a collision occurs, the distance between the molecular centers is \({\sigma }_{12}\). We can say that the center of molecule \(2\) is at a particular point on the surface of a sphere, of radius \({\sigma }_{12}\), circumscribed about molecule \(1\). As sketched in Figure 13, we can rotate the line of centers around the velocity vector, while keeping the angle between them constant at \(\theta\). As we do so, the line of centers traces out a circle on the surface of the sphere; collisions that put the center of molecule\(\ 2\) at any two points on this circle are completely equivalent. Letting the radius of this circle be \(r\), we see that \(r=\sigma_{12}\mathrm{sin} \theta\). Evidently, for spherical molecules, specifying \(\theta\) specifies the relative orientation at the time of collision.
If we now allow \(\theta\) to vary by \(d\theta\), the locus of equivalent points on the circumscribed sphere expands to a band. Measured along the surface of the sphere, the width of this band is \({\sigma }_{12}d\theta\). As molecule \(1\) moves through the gas of stationary type \(2\) molecules, this band sweeps out a cylindrical shell. Molecule \(1\) collides, at an angle between \(\theta\) and \(\theta +d\theta\), with every type \(2\) molecule in this cylindrical shell. Conversely, every type \(2\) molecule in this cylindrical shell collides with molecule \(1\) at an angle between \(\theta\) and \(\theta +d\theta\). (Molecule \(1\) also collides with many other type \(2\) molecules, but those collisions are at other angles; they have different orientations.) In unit time, the length of the cylindrical shell is \(v_{12}\). The volume of the cylindrical shell is its length times its cross-sectional area.
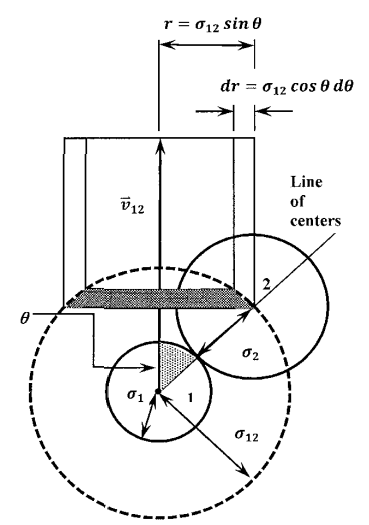
The cross-section of the cylindrical shell is a circular annulus. Viewing the annulus as a rectangular strip whose length is the circumference of the shell and whose width is the radial thickness of the annulus, the area of the annulus is the circumference times the radial thickness. Since the radius of the shell is \(r={\sigma }_{12}\mathrm{sin} \theta\), its circumference is \(2\pi {\sigma }_{12} \mathrm{sin} \theta\). The radial thickness of the annulus is just the change in the distance, \(r={\sigma }_{12}\mathrm{sin} \theta\), between the velocity vector and the wall of the cylinder when \(\theta\) changes by a small amount \(d\theta\). This is
\[dr=\left(\frac{dr}{d\theta }\right)d\theta ={\sigma }_{12} \mathrm{cos} \theta d\theta \nonumber \]
Therefore, the area of the annulus is
\[2\pi {\sigma }^2_{12} \mathrm{sin} \theta \mathrm{cos} \theta d\theta \nonumber \]
and the volume of the cylindrical shell swept out by a type 1 molecule (traveling at exactly the speed \(v_{12}\)) in unit time is
\[2\pi {\sigma }^2_{12}v_{12} \mathrm{sin} \theta \mathrm{cos} \theta d\theta \nonumber \]
We again let \(N_2\) be the number of molecules of type \(2\) per unit volume. The number of collisions, per unit time, between a molecule of type \(1\), traveling at exactly \(v_{12}\), and molecules of type \(2\), in which the collision angle lies between \(\theta\) and \(\theta +d\theta\) is
\[2\pi N_2{\sigma }^2_{12}v_{12} \mathrm{sin} \theta \mathrm{cos} \theta d\theta \nonumber \]
We need to find the number of such collisions in which the relative velocity lies between \(v_{12}\) and \(v_{12}+dv_{12}\). The probability of finding \(v_{12}\) in this interval is \(\left(df\left(v_{12}\right)/dv_{12}\right)dv_{12}\). Let \(d\widetilde{\nu }_{12}\left({\nu }_{12},\theta \right)\) be the number of collisions made in unit time, by a type \(1\) molecule, with molecules of type \(2\), in which the collision angle is between \(\theta\) and \(\theta +d\theta\), and the scalar relative velocity is between \(v_{12}\) and \(v_{12}+dv_{12}\). This is just the number of collisions when the relative velocity is \(v_{12}\) multiplied by the probability that the relative velocity is between \(v_{12}\) and \(v_{12}+dv_{12}\). We have the result we need:
\[ \begin{aligned} d\widetilde{\nu }_{12}\left(v_{12},\theta \right) & = 2\pi N_2{\sigma }^2_{12}v_{12}\left(\frac{df\left(v_{12}\right)}{dv_{12}}\right) \mathrm{sin} \theta ~ \mathrm{cos} \theta ~ d\theta dv_{12} \\ ~ & =8 { \pi }^2N_2{\sigma }^2_{12} \left(\frac{\mu }{2\pi kT}\right)^{3/2}v^3_{12}exp\left(\frac{-\mu v^2_{12}}{2kT}\right) \times \mathrm{sin} \theta ~ \mathrm{cos} \theta ~ d\theta dv_{12} \end{aligned} \nonumber \]
Recognizing that possible values of \(\theta\) lie in the range \(0\le \theta <{\pi }/{2}\) and that possible values of \(v_{12}\) lie in the range \(0\le v_{12}<\infty\), we can find the frequency of all possible collisions, \(\widetilde{\nu }_{12}\), by summing over all possible values of \(\theta\) and \(v_{12}\). That is,
\[\begin{aligned} \widetilde{\nu }_{12} & =8{\pi }^2N_2{\sigma }^2_{12} \left(\frac{\mu }{2\pi kT}\right)^{3/2}\int^{\infty }_0 v^3_{12}exp\left(\frac{-\mu v^2_{12}}{2kT}\right) dv_{12} \times \int^{\pi /2}_0 \mathrm{sin} \theta ~ \mathrm{cos} \theta ~ d\theta \\ ~ & =8{\pi }^2N_2{\sigma }^2_{12} \left(\frac{\mu }{2\pi kT}\right)^{3/2}\left[2 \left(\frac{kT}{\mu }\right)^2\right]\left[\frac{1}{2}\right] \\ ~ & =N_2{\sigma }^2_{12} \left(\frac{8\pi kT}{\mu }\right)^{1/2} \end{aligned} \nonumber \]
In Section 4.12, we obtained this result by a slightly different argument, in which we did not explicitly consider the collision angle, \(\theta\).


