3.11: The Variance of the Average- The Central Limit Theorem

Last updated
Save as PDF

Page ID: 151674

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

The central limit theorem establishes very important relationships between the statistics for two distributions that are related in a particular way. It enables us to understand some important features of physical systems.

The central limit theorem concerns the distribution of averages. If we have some original distribution and sample it three times, we can calculate the average of these three data points. Call this average \(A_{3,1}\). We could repeat this activity and obtain a second average of three values, \(A_{3,2}\). We can do this repeatedly, generating averages \(A_{3,3}\),…, \(A_{3,n}\). Several things will be true about these averages:

The set of all of the possible averages-of-three, \(\{{\boldsymbol{A}}_{\boldsymbol{3},\boldsymbol{i}}\}\), is itself a distribution. This averages-of-three distribution is different from the original distribution. Each average-of-three is a value of the random variable associated with the averages-of-three distribution.
Each of the \({\boldsymbol{A}}_{\boldsymbol{3},\boldsymbol{i}}\) is an estimate of the mean of the original distribution.
The distribution of the \({\boldsymbol{A}}_{\boldsymbol{3},\boldsymbol{i}}\) will be less spread out than the original distribution.

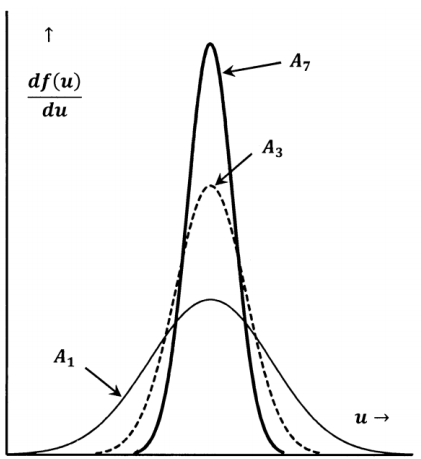
There is nothing unique about averaging three values. We could sample the original distribution seven times and compute the average of these seven values, calling the result \(A_{7,1}\). Repeating, we could generate averages \(A_{7,2}\),…, \(A_{7,m}\). All of the things we say about the averages-of-three are also true of these averages-of-seven. However, we can now say something more: The distribution of the \({\mathrm{A}}_{\mathrm{7,i}}\) will be less spread out than the distribution of the \({\mathrm{A}}_{\mathrm{3,i}}\). The corresponding probability density functions are sketched in Figure 13.

Screen Shot 2019-09-30 at 1.04.22 PM.png — Figure 13. The Variance of an Average of \(N\) is proportional to \(1/N\).

The central limit theorem relates the mean and variance of the distribution of averages to the mean and variance of the original distribution:

If random samples of \(\boldsymbol{N}\) values are taken from a distribution, whose mean is µ and whose variance is \({\boldsymbol{\sigma }}^{\boldsymbol{2}}\), averages of these \(\boldsymbol{N}\) values, \({\boldsymbol{A}}_{\boldsymbol{N}}\), are approximately normally distributed with a mean of µ and a variance of \(\boldsymbol{\sigma }^{\boldsymbol{2}}/\boldsymbol{N}\). The approximation to the normal distribution becomes better as \(\boldsymbol{N}\) becomes larger.

It turns out that the number, \(N\), of trials that is needed to get a good estimate of the variance is substantially larger than the number required to get a good estimate of the mean.