2.11: The Barometric Formula
- Page ID
- 151662
We can measure the pressure of the atmosphere at any location by using a barometer. A mercury barometer is a sealed tube that contains a vertical column of liquid mercury. The space in the tube above the liquid mercury is occupied by mercury vapor. Since the vapor pressure of liquid mercury at ordinary temperatures is very low, the pressure at the top of the mercury column is very low and can usually be ignored. The pressure at the bottom of the column of mercury is equal to the pressure of a column of air extending from the elevation of the barometer all the way to the top of the earth’s atmosphere. As we take the barometer to higher altitudes, we find that the height of the mercury column decreases, because less and less of the atmosphere is above the barometer.
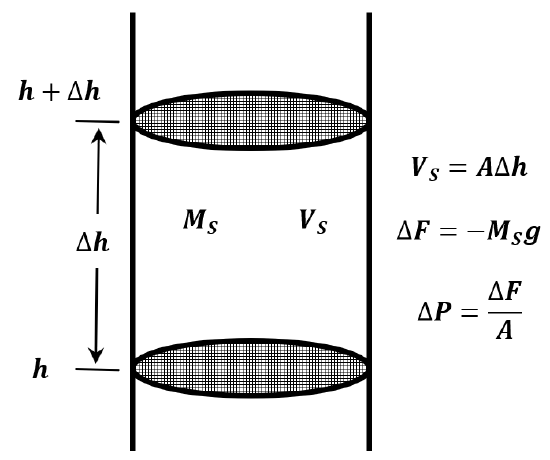
If we assume that the atmosphere is composed of an ideal gas and that its temperature is constant, we can derive an equation for atmospheric pressure as a function of altitude. Imagine a cylindrical column of air extending from the earth’s surface to the top of the atmosphere (Figure 4). The force exerted by this column at its base is the weight of the air in the column; the pressure is this weight divided by the cross-sectional area of the column. Let the cross-sectional area of the column be \(A\).
Consider a short section of this column. Let the bottom of this section be a distance \(h\) from the earth’s surface, while its top is a distance \(h+\Delta h\) from the earth’s surface. The volume of this cylindrical section is then \(V_S=A\Delta h\). Let the mass of the gas in this section be \(M_S\). The pressure at \(h+\Delta h\) is less than the pressure at \(h\) by the weight of this gas divided by the cross-sectional area. The weight of the gas is \(M_Sg\). The pressure difference is \(\Delta P=-{M_Sg}/{A}\). We have
\[\frac{P\left(h+\Delta h\right)-P\left(h\right)}{\Delta h}=\frac{\Delta P}{\Delta h}=\frac{-M_Sg}{A\Delta h}=\frac{-M_Sg}{V_S} \nonumber \]
Since we are assuming that the sample of gas in the cylindrical section behaves ideally, we have \(V_S={n_SRT}/{P}\). Substituting for \(V_S\) and taking the limit as \(\Delta h\to 0\), we find
\[\frac{dP}{dh}=\left(\frac{{-M}_Sg}{n_SRT}\right)P=\left(\frac{{-n}_S\overline{M}g}{n_SRT}\right)P=\left(\frac{-mg}{kT}\right)P \nonumber \]
where we introduce \(n_S\) as the number of moles of gas in the sample, \(\overline{M}\) as the molar mass of this gas, and \(m\) as the mass of an individual atmosphere molecule. The last equality on the right makes use of the identities \(\overline{M}=m\overline{N}\) and \(R=\overline{N}k\). Separating variables and integrating between limits \(P\left(0\right)=P_0\) and \(P\left(h\right)=P\), we find
\[\int^P_{P_0}{\frac{dP}{P}}=\left(\frac{-mg}{kT}\right)\int^h_0{dh} \nonumber \]
so that \[{ \ln \left(\frac{P}{P_0}\right)\ }=\frac{-mgh}{kT} \nonumber \]
and
\[P=P_0\mathrm{exp}\left(\frac{-mgh}{kT}\right) \nonumber \]
Either of the latter relationships is frequently called the barometric formula.
If we let \(\eta\) be the number of molecules per unit volume, \(\eta ={N}/{V}\), we can write \(P={NkT}/{V}=\eta kT\) and \(P_0={\eta }_0kT\) so that the barometric formula can be expressed in terms of these number densities as
\[\eta ={\eta }_0\mathrm{exp}\left(\frac{-mgh}{kT}\right) \nonumber \]


