2.10: Deriving Boyle's Law from Newtonian Mechanics
- Page ID
- 151830
We can derive Boyle’s law from Newtonian mechanics. This derivation assumes that gas molecules behave like point masses that do not interact with one another. The pressure of the gas results from collisions of the gas molecules with the walls of the container. The contribution of one collision to the force on the wall is equal to the change in the molecule’s momentum divided by the time between collisions. The magnitude of this force depends on the molecule’s speed and the angle at which it strikes the wall. Each such collision makes a contribution to the pressure that is equal to the force divided by the area of the wall. To find the pressure from this model, it is necessary to average over all possible molecular speeds and all possible collision angles. In Chapter 4, we derive Boyle’s law in this way.
We can do a simplified derivation by making a number of assumptions. We assume that all of the molecules in a sample of gas have the same speed. Let us call it \(u\). As sketched in Figure 3, we assume that the container is a cubic box whose edge length is \(d\). If we consider all of the collisions between molecules and walls, it is clear that each wall will experience \({1}/{6}\) of the collisions; or, each pair of opposing walls will experience \({\mathrm{1}}/{\mathrm{3}}\) of the collisions. Instead of averaging over all of the possible angles at which a molecule could strike a wall and all of the possible times between collisions, we assume that the molecules travel at constant speed back and forth between opposite faces of the box. Since they are point masses, they never collide with one another. If we suppose that \({\mathrm{1}}/{\mathrm{3}}\) of the molecules go back and forth between each pair of opposite walls, we can expect to accomplish the same kind of averaging in setting up our artificial model that we achieve by averaging over the real distribution of angles and speeds. In fact, this turns out to be the case; the derivation below gets the same result as the rigorous treatment we develop in Chapter 4.
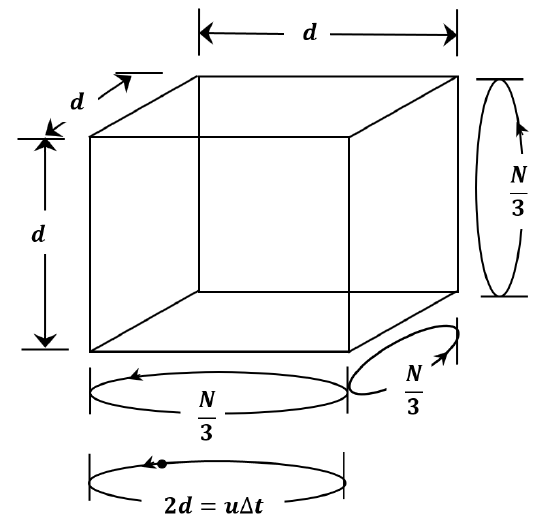
Since each molecule goes back and forth between opposite walls, it collides with each wall once during each round trip. At each collision, the molecule’s speed remains constant, but its direction changes by 180\({}^{o}\); that is, the molecule’s velocity changes from \(\mathop{u}\limits^{\rightharpoonup}\) to \(-\mathop{u}\limits^{\rightharpoonup}\). Letting \(\Delta t\) be the time required for a round trip, the distance traversed in a round trip is
\[\begin{aligned} 2d & =\left|\mathop{u}\limits^{\rightharpoonup}\right|\Delta t \\ ~ & =u\Delta t \end{aligned} \nonumber \]
The magnitude of the momentum change for a molecule in one collision is
\[\begin{align*} \left|\Delta (m\mathop{u}\limits^{\rightharpoonup})\right| &=\left|m{\mathop{u}\limits^{\rightharpoonup}}_{final}-m{\mathop{u}\limits^{\rightharpoonup}}_{initial}\right| \\[4pt] &=\left|m{\mathop{u}\limits^{\rightharpoonup}}_{final}-\left({-m\mathop{u}\limits^{\rightharpoonup}}_{final}\right)\right| \\[4pt] &=2mu \end{align*} \]
The magnitude of the force on the wall from one collision is
\[F=\frac{\left|\Delta \left(m\mathop{u}\limits^{\rightharpoonup}\right)\right|}{\Delta t}=\frac{2mu}{\left({2d}/{u}\right)}=\frac{mu^2}{d} \nonumber \]
and the pressure contribution from one collision on the wall, of area \(d^2\), is
\[P=\frac{F}{A}=\frac{mu^2}{d\bullet d^2}=\frac{{mu}^2}{d^3}=\frac{{mu}^2}{V} \nonumber \]
so that we have
\[PV=mu^2 \nonumber \]
from the collision of one molecule with one wall.
If the number of molecules in the box is \(N\), \(N/3\) of them make collisions with this wall, so that the total pressure on one wall attributable to all \(N\) molecules in the box is
\[P=\frac{mu^2}{V}\frac{N}{3} \nonumber \]
or
\[PV=\frac{Nmu^2}{3} \nonumber \]
Since the ideal gas equation can be written as \(PV=NkT\) we see that \({Nmu^2}/{3}=NkT\) so that \(mu^2=3kT\) and
\[u=\sqrt{\frac{3kT}{m}} \nonumber \]
Thus we have found a relationship between the molecular speed and the temperature of the gas. (The actual speed of a molecule, \(v\), can have any value between zero and—for present purposes—infinity. When we average the values of \(v^2\) for many molecules, we find the average value of the squared speeds, \(\overline{v^2}\). In Chapter 4, we find that \(u^2=\overline{v^2}\). That is, the average speed we use in our derivation turns out to be a quantity called the root-mean-square speed, \(v_{rms}=u=\sqrt{\overline{v^2}}\).) This result also gives us the (average) kinetic energy of a single gas molecule:
\[KE=\frac{mu^2}{2}=\frac{3kT}{2} \nonumber \]
From this derivation, we have a simple mechanical model that explains Boyle’s law as the logical consequence of point-mass molecules colliding with the walls of their container. By combining this result with the ideal gas equation, we find that the average speed of ideal gas molecules depends only on the temperature. From this we have the very important result that the translational kinetic energy of an ideal gas depends only on temperature.
Since our non-interacting point-mass molecules have no potential energy arising from their interactions with one another, their translational kinetic energy is the whole of their energy. (Because two such molecules neither attract nor repel one another, no work is required to change the distance between them. The work associated with changing the volume of a confined sample of an ideal gas arises because of the pressure the molecules exert on the walls of the container; the pressure arises because of the molecules’ kinetic energy.) The energy of one mole of monatomic ideal gas molecules is
\[KE=\left({3}/{2}\right)RT \nonumber \]
When we expand our concept of ideal gases to include molecules that have rotational or vibrational energy, but which neither attract nor repel one another, it remains true that the energy of a macroscopic sample depends only on temperature. However, the molar energy of such a gas is greater than \(\left({3}/{2}\right)RT\), because of the energy associated with these additional motions.
We make extensive use of the conclusion that the energy of an ideal gas depends only on temperature. As it turns out, this conclusion follows rigorously from the second law of thermodynamics. In Chapter 10, we show that
\[{\left(\frac{\partial E}{\partial V}\right)}_T={\left(\frac{\partial E}{\partial P}\right)}_T=0 \nonumber \]
for a substance that obeys the ideal gas equation; at constant temperature, the energy of an ideal gas is independent of the volume and independent of the pressure. So long as pressure, volume, and temperature are the only variables needed to specify its state, the laws of thermodynamics imply that the energy of an ideal gas depends only on temperature.
While the energy of an ideal gas is independent of pressure, the energy of a real gas is a function of pressure at a given temperature. At ordinary pressures and temperatures, this dependence is weak and can often be neglected. The first experimental investigation of this issue was made by James Prescott Joule, for whom the SI unit of energy is named. Beginning in 1838, Joule did a long series of careful measurements of the mechanical equivalent of heat. These measurements formed the original experimental basis for the kinetic theory of heat. Among Joule’s early experiments was an attempt to measure the heat absorbed by a gas as it expanded into an evacuated container, a process known as a free expansion. No absorption of heat was observed, which implied that the energy of the gas was unaffected by the volume change. However, it is difficult to do this experiment with meaningful accuracy.
Subsequently, Joule collaborated with William Thomson (Lord Kelvin) on a somewhat different experimental approach to essentially the same question. The Joule-Thomson experiment provides a much more sensitive measure of the effects of intermolecular forces of attraction and repulsion on the energy of a gas during its expansion. Since our definition of an ideal gas includes the stipulation that there are no intermolecular forces, the Joule-Thomson experiment is consistent with the conclusion that the energy of an ideal gas depends only on temperature. However, since intermolecular forces are not zero for any real gas, our analysis reaches this conclusion in a somewhat indirect way. The complication arises because the Joule-Thomson results are not entirely consistent with the idea that all properties of a real gas approach those of an ideal gas at a sufficiently low pressure. (The best of models can have limitations.) We discuss the Joule-Thomson experiment in Section 10.14.


