1.18: Bonding in Diatomics
- Page ID
- 9341
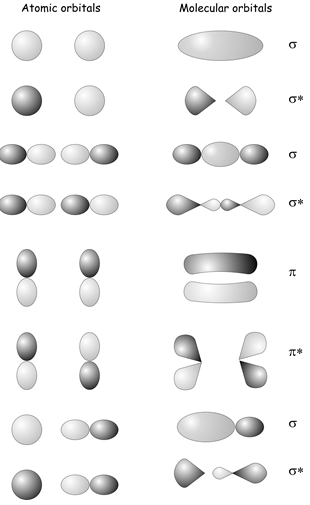 You will already be familiar with the idea of constructing molecular orbitals from linear combinations of atomic orbitals from previous courses covering bonding in diatomic molecules. By considering the symmetries of \(s\) and \(p\) orbitals on two atoms, we can form bonding and antibonding combinations labeled as having either \(\sigma\) or \(\pi\) symmetry depending on whether they resemble \(s\) or \(p\) orbitals when viewed along the bond axis (see diagram below). In all of the cases shown, only atomic orbitals that have the same symmetry when viewed along the bond axis \(z\) can form a chemical bond e.g. two \(s\) orbitals, two \(p_z\) orbitals , or an \(s\) and a \(p_z\) can form a bond, but a \(p_z\) and a \(p_x\) or an \(s\) and a \(p_x\) or a \(p_y\) cannot. It turns out that the rule that determines whether or not two atomic orbitals can bond is that they must belong to the same symmetry species within the point group of the molecule.
You will already be familiar with the idea of constructing molecular orbitals from linear combinations of atomic orbitals from previous courses covering bonding in diatomic molecules. By considering the symmetries of \(s\) and \(p\) orbitals on two atoms, we can form bonding and antibonding combinations labeled as having either \(\sigma\) or \(\pi\) symmetry depending on whether they resemble \(s\) or \(p\) orbitals when viewed along the bond axis (see diagram below). In all of the cases shown, only atomic orbitals that have the same symmetry when viewed along the bond axis \(z\) can form a chemical bond e.g. two \(s\) orbitals, two \(p_z\) orbitals , or an \(s\) and a \(p_z\) can form a bond, but a \(p_z\) and a \(p_x\) or an \(s\) and a \(p_x\) or a \(p_y\) cannot. It turns out that the rule that determines whether or not two atomic orbitals can bond is that they must belong to the same symmetry species within the point group of the molecule.
We can prove this mathematically for two atomic orbitals \(\phi_i\) and \(\phi_j\) by looking at the overlap integral between the two orbitals.
\[S_{ij} = \langle \phi_i|\phi_j \rangle = \int \phi_i^* \phi_j d\tau \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \text(18.1)\]
In order for bonding to be possible, this integral must be non-zero. The product of the two functions \(\phi_1\) and \(\phi_2\) transforms as the direct product of their symmetry species i.e. \(\Gamma_{12}\) = \(\Gamma_1 \otimes \Gamma_2\). As explained above, for the overlap integral to be non-zero, \(\Gamma_{12}\) must contain the totally symmetric irreducible representation (\(A_{1g}\) for a homonuclear diatomic, which belongs to the point group \(D_{\infty h}\)). As it happens, this is only possible if \(\phi_1\) and\(\phi_2\) belong to the same irreducible representation. These ideas are summarized for a diatomic in the table below.
\[\begin{array}{lllll} \hline \text{First Atomic Orbital} & \text{Second Atomic Orbital} & \Gamma_1 \otimes \Gamma_2 & \text{Overlap Integral} & \text{Bonding?} \\ \hline s \: (A_{1g}) & s \: (A_{1g}) & A_{1g} & \text{Non-zero} & \text{Yes} \\ s \: (A_{1g}) & p_x \: (E_{1u}) & E_{1u} & \text{Zero} & \text{No} \\ s \: (A_{1g}) & p_z \: (A_{1u}) & A_{1u} & \text{Zero} & \text{No} \\ p_x \: (E_{1u}) & p_x \: (E_{1u}) & A_{1g} + A_{2g} + E_{2g} & \text{Non-zero} & \text{Yes} \\ p_X \: (E_{1u}) & p_z \: (A_{1u}) & E_{1g} & \text{Zero} & \text{No} \\ p_z \: (A_{1u}) & p_z \: (A_{1u}) & A_{1g} & \text{Non-zero} & \text{Yes} \end{array} \tag{18.2}\]


