1.9: Transformation matrices
- Page ID
- 9333
Matrices can be used to map one set of coordinates or functions onto another set. Matrices used for this purpose are called transformation matrices. In group theory, we can use transformation matrices to carry out the various symmetry operations considered at the beginning of the course. As a simple example, we will investigate the matrices we would use to carry out some of these symmetry operations on a vector \(\begin{pmatrix} x, y \end{pmatrix}\).
The identity Operation
The identity operation leaves the vector unchanged, and as you may already suspect, the appropriate matrix is the identity matrix.
\[\begin{pmatrix} x, y \end{pmatrix} \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} x, y \end{pmatrix} \label{9.1}\]
Reflection in a plane
The simplest example of a reflection matrix corresponds to reflecting the vector \(\begin{pmatrix} x, y \end{pmatrix}\) in either the \(x\) or \(y\) axes. Reflection in the \(x\) axis maps \(y\) to \(-y\), while reflection in the \(y\) axis maps \(x\) to \(-x\). The appropriate matrix is very like the identity matrix but with a change in sign for the appropriate element. Reflection in the \(x\) axis transforms the vector \(\begin{pmatrix} x, y \end{pmatrix}\) to \(\begin{pmatrix} x, -y \end{pmatrix}\), and the appropriate matrix is
\[\begin{pmatrix} x, y \end{pmatrix} \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} = \begin{pmatrix} x, -y \end{pmatrix} \label{9.2}\]
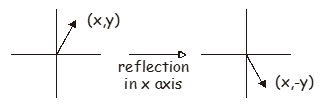
Reflection in the y axis transforms the vector \(\begin{pmatrix} x, y \end{pmatrix}\) to \(\begin{pmatrix} -x, y \end{pmatrix}\), and the appropriate matrix is
\[\begin{pmatrix} x, y \end{pmatrix} \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} -x, y \end{pmatrix} \label{9.3}\]
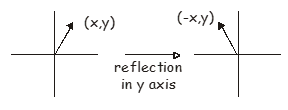
More generally, matrices can be used to represent reflections in any plane (or line in 2D). For example, reflection in the 45° axis shown below maps
\(\begin{pmatrix} x, y \end{pmatrix}\) onto \(\begin{pmatrix} -y, -x \end{pmatrix}\).
\[\begin{pmatrix} x, y \end{pmatrix} \begin{pmatrix} 0 & -1 \\ -1 & 0 \end{pmatrix} = \begin{pmatrix} -y, -x \end{pmatrix} \label{9.4}\]

Rotation about an Axis
In two dimensions, the appropriate matrix to represent rotation by an angle \(\theta\) about the origin is
\[R(\theta) = \begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix} \label{9.5}\]
In three dimensions, rotations about the \(x\), \(y\) and \(z\) axes acting on a vector \(\begin{pmatrix} x, y, z \end{pmatrix}\) are represented by the following matrices.
\[R_{x}(\theta) = \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{pmatrix} \label{9.6a}\]
\[R_{y}(\theta) = \begin{pmatrix} \cos\theta & 0 & -\sin\theta \\ 0 & 1 & 0 \\ \sin\theta & 0 & \cos\theta \end{pmatrix} \label{9.6b}\]
\[R_{z}(\theta) = \begin{pmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{pmatrix} \label{9.6c}\]


