6.1: Classification of Overlayer Structures
- Page ID
- 25387
Adsorbed species on single crystal surfaces are frequently found to exhibit long-range ordering ; that is to say that the adsorbed species form a well-defined overlayer structure. Each particular structure may only exist over a limited coverage range of the adsorbate, and in some adsorbate/substrate systems a whole progression of adsorbate structures are formed as the surface coverage is gradually increased.
This section deals with the classification of such ordered structures - in most cases this involves describing the overlayer structure in terms of the underlying structure of the substrate.
There are two principal methods for specifying the structure:
- Wood's notation
- matrix notation.
Before we start to discuss overlayer structures, however, we need to make sure that we can adequately describe the structure of the substrate !
The Concept of the Surface Unit Cell
The primitive unit cell is the simplest periodically repeating unit which can be identified in an ordered array - the array in this instance being the ordered arrangement of surface atoms. By repeated translation of a unit cell, the whole array can be constructed. Let us consider the clean surface structures of the low index surface planes of fcc metals.
The fcc (100) surface
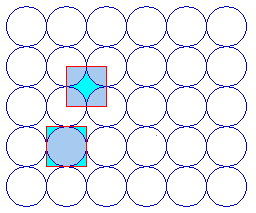
The fcc(100) surface has 4-fold rotational symmetry ("square symmetry") - perhaps it should not surprise us therefore to find that the primitive unit cell for this surface is square in shape !
fcc(100) surface
Two possible choices of unit cell are highlighted - it is clear that a unit cell of this size is indeed going to be the simplest possible repeating unit for this surface. The two alternatives drawn are in fact but two of an infinite number of possibilities; they have the same shape/symmetry, size and orientation, differing only in their translational position or "origin".
Whichever we choose then it is clear that we can indeed generate the whole surface structure by repeated translation of the unit cell; for example ....
In fact, I personally prefer the alternative choice of unit cell which has the corners of the unit cell coincident with the atomic centres.
We now need to think how to define the unit cell shape, size and symmetry - this is best done using two vectors which have a common origin and define two sides of the unit cell ...
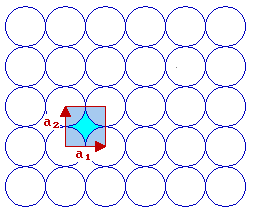
For this fcc(100) surface the two vectors which define the unit cell, conventionally called a1 & a2, are:
- the same length i.e. |a1| = |a2|
- mutually perpendicular
By convention, one also selects the vectors such that you go anticlockwise from a1 to get to a2 .
The length of the vectors a1 & a2 is related to the bulk unit cell parameter, a, by |a1| = |a2| = a / √2 ]
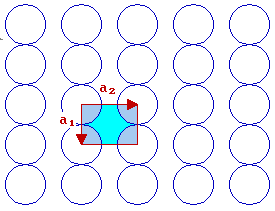
The fcc (110) surface
In the case of the fcc(110) surface, which has 2-fold rotational symmetry, the unit cell is rectangular
fcc(110) surface
By convention, |a2| > |a1| - if we also recall the convention that one goes anticlockwise to get from a1 to a2, then this leads to the choice of vectors shown.
The fcc (111) surface
With the fcc (111) surface we again have a situation where the length of the two vectors are the same i.e. | a1| = | a2| . We can either keep the angle between the vectors less than 90 degrees or let it be greater than 90 degrees. The normal convention is to choose the latter, i.e. the right hand cell of the two illustrated with an angle of 120 degrees between the two vectors.
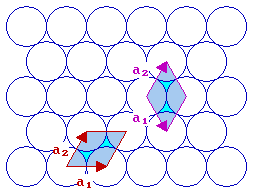
fcc(111) surface
Overlayer Structures
If we have an ordered overlayer of adsorbed species (atoms or molecules), then we can use the same basic ideas as outlined in the previous section to define the structure. The adsorbate unit cell is usually defined by the two vectors b1 and b2 . To avoid ambiguities, it again helps if we stick to a set of conventions in choosing the unit cell vectors. In this case:
- b2 is again selected to be anticlockwise from b1 .
- if possible, b1 is chosen to be parallel to a1 and b2 parallel to a2 .
Once the unit cell vectors for substrate and adsorbate have been selected then it is a relatively simple matter to work out how to denote the structure.
Wood's Notation
Wood's notation is the simplest and most frequently used method for describing a surface structure - it only works, however, if the two unit cells are of the same symmetry or closely-related symmetries (more specifically, the angle between b1 & b2 must be the same as that between a1 & a2 ).
In essence, Wood's notation first involves specifying the lengths of the two overlayer vectors, b1 & b2, in terms of a1 & a2 respectively - this is then written in the format:
\[( |b_1|/|a_1| \times |b_2|/|a_2| )\]
i.e. a ( 2 x 2 ) structure has |b1| = 2|a1| and |b2| = 2|a2| .
The following diagram shows a ( 2 x 2 ) adsorbate overlayer on an fcc(100) surface in which the adsorbate is bonded terminally on-top of individual atoms of the substrate.
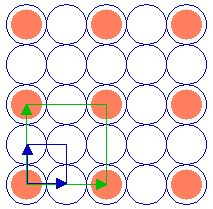
Substrate: fcc(100)
Substrate unit cell
Adsorbate unit cell
The unit cells of the (100) substrate and the ( 2 x 2 ) overlayer are both highlighted.
The next diagram shows another ( 2 x 2 ) structure, but in this case the adsorbate species is bonded in the four-fold hollows of the substrate surface. Of course, only a very limited section of the structure can be shown here - in practice, the unit cell shown would repeat to give a complete overlayer structure extending across the substrate surface.
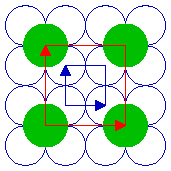
Substrate: fcc(100)
Substrate unit cell
Adsorbate unit cell
The highlighted unit cells of the adsorbate and substrate are identical in size, shape and orientation to those of the previously illustrated ( 2 x 2 ) structure. Both this and the previous structure are examples of primitive ( 2 x 2 ), or p( 2 x 2 ), structures. That is to say that they are indeed the simplest unit cells that may be used to describe the overlayer structure, and contain only one "repeat unit". For the purposes of this tutorial I shall follow common practice and omit the preceding "p" - referring to such structures simply as ( 2 x 2 ) structures (in spoken language, "two by two" structures).
Such ( 2 x 2 ) structures are also found on other surfaces, but they may differ markedly in superficial appearance from the structure on the fcc(100) surface. The following diagram, for example, shows a ( 2 x 2 ) structure on a fcc(110) surface
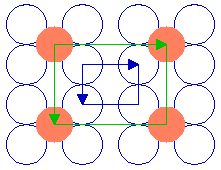
Substrate: fcc(110)
Substrate unit cell
Adsorbate unit cell
The adsorbate unit cell is again twice as large as that of the substrate in both dimensions - it retains the same aspect ratio as the rectangular substrate unit cell (1: 1.414) and does not exhibit any rotation with respect to the substrate cell. The following diagram shows yet another ( 2 x 2 ) structure, in this case on the fcc(111) surface ...
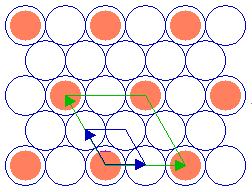
Substrate: fcc(111)
Substrate unit cell
Adsorbate unit cell
Again, the adsorbate unit cell is of the same symmetry as the substrate cell but is scaled up by a factor of two in its linear dimensions (and corresponds to a surface area four times as large as that of the substrate unit cell).
The next example is a surface structure which is closely related to the ( 2 x 2 ) structure: it differs in that there is an additional atom in the middle/centre of the ( 2 x 2 ) adsorbate unit cell. Since the middle atom is "crystallographically equivalent" to those at the corners (i.e. it is not distinguishable by means of different coordination to the underlying substrate or any other structural feature), then this is no longer a primitive ( 2 x 2 ) structure.
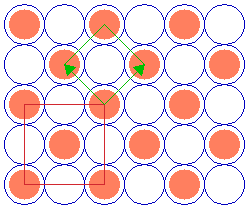
Substrate: fcc(100)
c( 2 x 2 )
(![]() 2 x
2 x ![]() 2)R45
2)R45
Instead it may be classified in one of two ways:
- As a centered ( 2 x 2 ) structure i.e. c( 2 x 2 ) [ where we are using a non-primitive unit cell containing 2 repeat units ]
- As a " (
 2 x
2 x  2)R45 " structure, where we are specifying the true primitive unit cell .
2)R45 " structure, where we are specifying the true primitive unit cell .
In using the latter Wood's notation we are stating that the adsorbate unit cell is a factor of ![]() 2 larger than the substrate unit cell in both directions and is also rotated by 45 degrees with respect to the substrate unit cell.
2 larger than the substrate unit cell in both directions and is also rotated by 45 degrees with respect to the substrate unit cell.
If the "central" atom is not completely crystallographically equivalent, then the structure formally remains a p(2x2) unit cell but now has a basis of two adsorbate atoms per unit cell.
In some instances it is possible to use a centred unit cell description for a structure for which the primitive unit cell cannot be described using Wood's notation - for example, the c( 2 x 2 ) structure on the fcc(110) surface shown below.
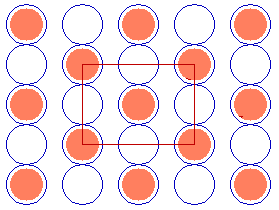
Substrate: fcc(110)
c( 2 x 2 )
As a final example, the next diagram illustrates a commonly-observed structure on fcc(111) surfaces which can be readily described using Wood's notation.
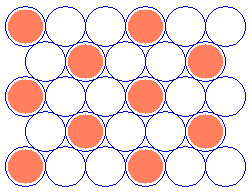
Substrate: fcc(111) (![]() 3 x
3 x ![]() 3)R30
3)R30
(You should confirm for yourself that the adsorbate unit cell is indeed scaled up from the substrate cell by the factor given and rotated by 30 degrees ! )
Matrix Notation
This is a much more general system of describing surface structures which can be applied to all ordered overlayers: quite simply it relates the vectors b1 & b2 to the substrate vectors a1 & a2 using a simple matrix i.e.
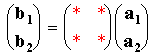
Matrix Notation: remember a1, a2, b1 and b2 are vectors.
To illustrate the use of matrix notation we shall now consider two surface structures with which we are already familiar ...

Substrate: fcc (100)
(2 x 2) overlayer
For the (2 x 2) structure we have:
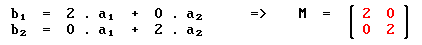
By contrast, for the c(2 x 2) structure:
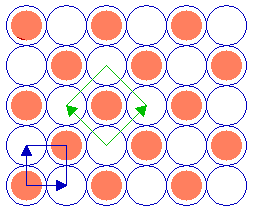
Substrate: fcc (100) c(2 x 2) overlayer
we have
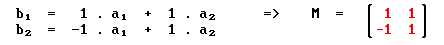
Summary
Ordered surface structures may be described by defining the adsorbate unit cell in terms of that of the underlying substrate using:
- Wood's Notation: in which the lengths of b1 and b2 are given as simple multiples of a1 and a2 respectively, and this is followed by the angle of rotation of b1 from a1 (if this is non-zero).
- Matrix Notation: in which b1 and b2 are independently defined as linear combinations of a1 and a2 and these relationships are expressed in a matrix format.


