9.4: The Variational Method
- Page ID
- 4538
In this section we introduce the powerful and versatile variational method and use it to improve the approximate solutions we found for the helium atom using the independent electron approximation. One way to take electron-electron repulsion into account is to modify the form of the wavefunction. A logical modification is to change the nuclear charge, Z, in the wavefunctions to an effective nuclear charge, from +2 to a smaller value, \(\zeta\) (called zeta) or \(Z_{eff}\). The rationale for making this modification is that one electron partially shields the nuclear charge from the other electron, as shown in Figure \(\PageIndex{1}\).

A region of negative charge density between one of the electrons and the +2 nucleus makes the potential energy between them more positive (decreases the attraction between them). We can effect this change mathematically by using \(\zeta < 2\) in the wavefunction expression. If the shielding were complete, then \(\zeta\) would equal 1. If there is no shielding, then \(\zeta = 2\). So a way to take into account the electron-electron interaction is by saying it produces a shielding effect. The shielding isn't zero, and it isn't complete, so the effective nuclear charge is between one and two.
In general, a theory should be able to make predictions in advance of knowledge of the experimental result. Consequently, a principle and method for choosing the best value for \(\zeta\) or any other adjustable parameter that is to be optimized in a calculation is needed. The Variational Principle provides the required criterion and method. The Variational Principle says that the best value for any variable parameter in an approximate wavefunction is the value that gives the lowest energy for the ground state; i.e., the value that minimizes the energy. The variational method is the procedure that is used to find the lowest energy and the best values for the variable parameters.
The variational principle means that the expectation value for the binding energy obtained using an approximate wavefunction and the exact Hamiltonian operator will be higher than or equal to the true energy for the system. This idea is really powerful. When implemented, it permits us to find the best approximate wavefunction from a given wavefunction that contains one or more adjustable parameters, called a trial wavefunction. A mathematical statement of the variational principle is
\[ \left \langle E_{trial} \right \rangle \ge E_{true} \label {9-31}\]
where
\[ \left \langle E_{trial} \right \rangle = \dfrac {\int \psi _{trial} ^* \hat {H} \psi _{trial} d \tau}{\int \psi _{trial} ^* \psi _{trial} d\tau } \label {9-32}\]
Often the expectation value and normalization integrals in Equation \(\ref{9-32}\) can be evaluated analytically. For the case of He described above, the trial wavefunction is the product wavefunction given by Equation \ref{9-13}:
\[\psi (r_1 , r_2) \approx \varphi (r_1) \varphi (r_2) \label {9-13}\]
the adjustable or variable parameter in the trial wavefunction is the effective nuclear charge \(\zeta\), and the Hamiltonian is the complete form given below.
\[\hat {H} = -\dfrac {\hbar ^2}{2m} \nabla^2_1 - \dfrac {\zeta e^2}{4 \pi \epsilon _0 r_1} - \dfrac {\hbar ^2}{2m} \nabla ^2_2 - \dfrac {\zeta e^2}{4 \pi \epsilon _0 r_2} + \dfrac {e^2}{4 \pi \epsilon _0 r_12} \label {9-9}\]
When the expectation value for the trial energy is calculated for helium, the result is a function that depends on the adjustable parameter, \(\zeta\).
\[ E_{trial} (\zeta) = \dfrac {\mu e^4}{4 \epsilon ^2_0 h} \left ( \zeta ^2 - \dfrac {27}{8} \zeta \right ) \label {9-33}\]
This function is shown in Figure \(\PageIndex{2}\). According to the variation principle, the minimum value of the energy on this graph is the best approximation of the true energy of the system, and the associated value of \(\zeta\) is the best value for the adjustable parameter.
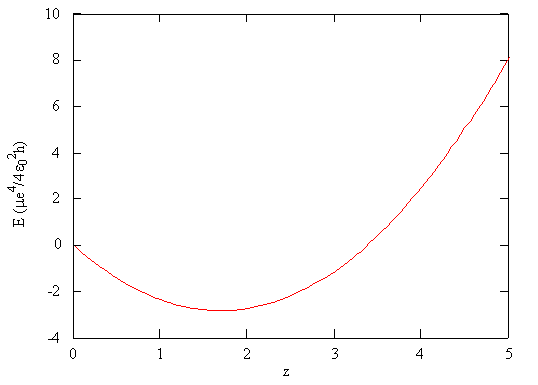
According to the variation principle, the minimum value of the variational energy (Equation \(\ref{9-32}\)) of a trial wavefunction is the best approximation of the true energy of the system.
Using the mathematical function for the energy of a system, the minimum energy with respect to the adjustable parameter can be found by taking the derivative of the energy with respect to that parameter, setting the resulting expression equal to zero, and solving for the parameter, in this case \(\zeta\). This is a standard method in calculus for finding maxima and minima.
Exercise \(\PageIndex{2}\)
Find the value for \(\zeta\) that minimizes the helium binding energy and compare the binding energy to the experimental value. What is the percent error in the calculated value?
When this procedure is carried out for He, we find \(\zeta = 1.6875\) and the approximate energy we calculate using this third approximation method, \(E \approx = -77.483\; eV\). Table \(\PageIndex{1}\) show that a substantial improvement in the accuracy of the computed binding energy is obtained by using shielding to account for the electron-electron interaction. Including the effect of electron shielding in the wavefunction reduces the error in the binding energy to about 2%. This idea is very simple, elegant, and significant.
|
|
|
|---|---|
|
|
|
| First-order Perturbation |
|
|
|
|
|
|
|
The improvement we have seen in the total energy calculations using a variable parameter \(\zeta\) indicates that an important contribution of electron-electron interaction or repulsion to the total binding energy arises from the fact that each electron shields the nuclear charge from the other electron. It is reasonable to assume the electrons are independent; i.e., that they move independently, but the shielding must be taken into account in order to fine-tune the wavefunctions. The inclusion of optimizable parameters in the wavefunction allows us to develop a clear physical image of the consequences of our variation calculation. Calculating energies correctly is important, and it is also important to be able to visualize electron densities for multi-electron systems. In the next two sections, we take a temporary break from our consideration of approximation methods in order to examine multi-electron wavefunctions more closely.


