8.7: Spin-Orbitals and Electron Configurations
- Page ID
- 4525
The wavefunctions obtained by solving the hydrogen atom Schrödinger equation are associated with orbital angular motion and are often called spatial wavefunctions, to differentiate them from the spin wavefunctions. The complete wavefunction for an electron in a hydrogen atom must contain both the spatial and spin components. We refer to the complete one-electron orbital as a spin-orbital and a general form for this orbital is
\[ | \varphi _{n,l,m_l , m_s} \rangle = | \psi _{n,l,m_l} (r, \theta , \psi ) \rangle | \sigma ^{m_s}_s \rangle \label {8.7.1}\]
A spin-orbital for an electron in the \(2p_z\) orbital with \(m_s = + \frac {1}{2} \), for example, could be written as
\[ | \psi _{2pz_\alpha} \rangle = | \psi _{2,1,0} (r, \theta \psi) \ | \alpha \rangle \label{8.7.2}\]
A common method of depicting electrons in spin-orbitals arranged by energy is shown in Figure \(\PageIndex{1}\), which gives one representation of the ground state electron configuration of the hydrogen atom.
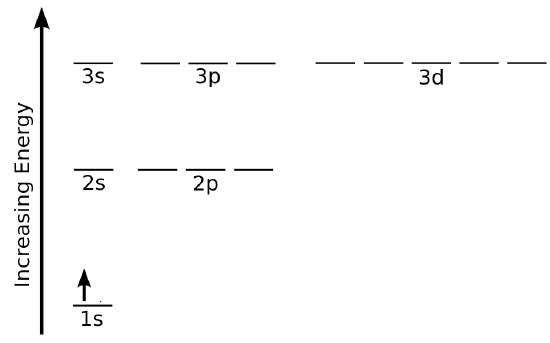
On the energy level diagram in Figure \(\PageIndex{1}\), the horizontal lines labeled 1s, 2s, 2p, etc. denote the spatial parts of the orbitals, and an arrow pointing up for spin \(\alpha\) and down for spin \(\beta \) denotes the spin part of the wavefunction.
An alternative shorthand notation for electron configuration is the familiar form 1s1 to denote an electron in the 1s orbital. Note that this shorthand version contains information only about the spatial wavefunction; information about spin is implied. Two electrons in the same orbital have spin \(\alpha\) and \(\beta \), e.g. 1s2, and one electron in an orbital is assumed to have spin \(\alpha\). Hydrogen atoms can absorb energy and the electron can be promoted to higher energy spin-orbitals. Examples of such excited state configurations are \(2p_1\), \(3d_1\), etc.


