2.2: Black-Body Radiation
- Page ID
- 4470
One experimental phenomenon that could not be adequately explained by classical physics was black-body radiation. Hot objects emit electromagnetic radiation. The burners on most electric stoves glow red at their highest setting. If we take a piece of metal and heat it in a flame, it begins to glow, dark red at first, then perhaps white or even blue if the temperature is high enough. A very hot object would emit a significant amount of energy in the ultraviolet region of the spectrum, and people are emitters of energy on the other end of the spectrum. We can see this infrared energy by using night vision goggles. The exact spectrum depends upon properties of the material and the temperature. A black-body is an ideal object that emits all frequencies of radiation with a spectral distribution that depends only on the temperature and not on its composition. The radiation emitted by such an object is called black-body radiation. Black-body radiation can be obtained experimentally from a pinhole in a hollow cavity that is held at a constant temperature.
It was found that the observed intensity of black-body radiation as a function of wavelength varies with temperature. Attempts to explain or calculate this spectral distribution from classical theory were complete failures. A theory developed by Rayleigh and Jeans predicted that the intensity should go to infinity at short wavelengths. Since the intensity actually drops to zero at short wavelengths, the Rayleigh-Jeans result was called the “ultraviolet catastrophe.” There was no agreement between theory and experiment in the ultraviolet region of the black-body spectrum. This is shown in Figure \(\PageIndex{1}\).
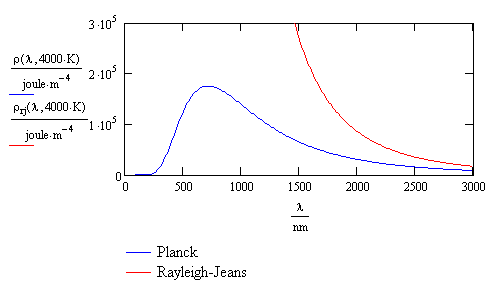
Max Planck was the first to successfully explain the spectral distribution of black-body radiation. He said that the radiation resulted from oscillations of electrons. Similarly, oscillations of electrons in an antenna produce radio waves. With revolutionary insight and creativity, Planck realized that in order to explain the spectral distribution, he needed to assume that the energy E of the oscillating electrons was quantized and proportional to integer multiples of the frequency ν
\[ E = nh \nu \label{2-1}\]
where n is an integer and h is a proportionality constant. He then was able to derive an equation (Equation \(\ref{2-2}\)) that gave excellent agreement with the experimental observations for all temperatures provided that the value of \(6.62618 \times 10^{-34}\) Joule.sec was used for h. This new fundamental constant, which is an essential component of Quantum Mechanics, now is called Planck’s constant. The Boltzmann constant, \(k_B\), and the speed of light (c), also appear in the equation.
\[\rho (\lambda, T) d \lambda = \frac {8 \pi hc}{\lambda ^5} \frac {d \lambda}{ e^{\frac {hc}{\lambda k_B T}} - 1} \label{2-2}\]
Example \(\PageIndex{1}\)
Use Equation to show that the units of ρ(λ,T)dλ are \(J/m^3\) as expected for an energy density.
Equation \(\ref{2-2}\) gives ρ(λ,T)dλ, the radiation density (\(J/m^3\)) between λ and λ + dλ inside the cavity from which the black-body radiation is emitted. The parameters in the equation are Planck’s constant, the speed of light, Boltzmann’s constant, the temperature, and the wavelength. The agreement between Planck’s theory and the experimental observation provided strong evidence that the energy of electron motion in matter is quantized. In the next two sections, we will see that the energy carried by light also is quantized in units of h \(\bar {\nu}\). These packets of energy are called “photons.”
Example \(\PageIndex{2}\)
Use Planck’s equation to prepare computer-generated graphs showing how ρ(λ,T), which is the black-body radiation density per nm, varies with wavelength at various temperatures. Use these graphs to explain why white hot is hotter than red hot. A Mathcad file link is provided as a head start for this exercise.
Example \(\PageIndex{3}\)
Use the results from Exercise \(\PageIndex{2}\) to prepare a computer-generated graph of \(λ_{max}\), which is the peak (or maximum) of the functions plotted in Exercise \(\PageIndex{1}\), as a function of T. Describe how the color of the light emitted from the black-body varies with temperature.
Example \(\PageIndex{4}\)
Use the results from Exercise \(\PageIndex{4}\) to estimate the color temperature of sunlight (that has a maximum at 480 nm) and the temperature of a tungsten light bulb (that has a maximum at 1035 nm.)


