22.4.2: ii. Problems
- Page ID
- 84721
Q1
Suppose you are given two molecules (one is \(CH_2\) and the other is \(CH_2^-\) but you don't know which is which). Both molecules have \(C_{2v}\) symmetry. The CH bond length of molecule I is 1.121 Å and for molecule II it is 1.076 Å. The bond angle of molecule I is 104\(^\circ\) and for molecule II it is 136\(^\circ\).
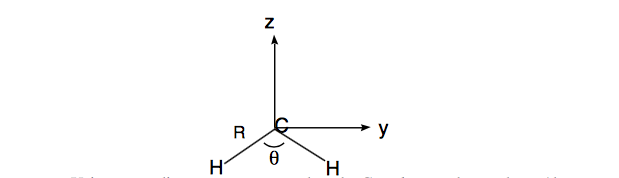
a. Using a coordinate system centered on the C nucleus as shown above (the molecule is in the YZ plane), compute the moment of inertia tensors of both species (I and II). The definitions of the componenets of the tensor are, for example:
\begin{align} I_{xx} &=& & \sum\limits_j m_j (y_j^2 + z_j^2) - M(Y^2 + Z^2) \\ I_{xy} &=& & -\sum\limits_j m_jx_jy_j - MXY \end{align}
Here, \(m_j\) is the mass of the nucleus j, M is the mass of the entire molecule, and X, Y, Z are the coordinates of the center of mass of the molecule. Use Å for distances and amu's for masses.
b. Find the principal moment of interia \(I_a \langle I_b \langle I_c\) for both compounds ( in amu Å\(^2\) units) and convert these values into rotational constants A, B, and C in \(cm^{-1}\) using, for example,
\[ A = \dfrac{h}{8\pi^2cI_a}. \nonumber \]
c. Both compounds are "nearly prolate tops" whose energy levels can be well approximated using the prolate top formula:
\[ E = (A - B) K^2 + B J(J + 1), \nonumber \]
if one uses for the B constant the average of the B and C valued determined earlier. Thus, take B and C values (for each compound) and average them to produce an effective B constant to use in the above energy formula. Write down ( in \(cm^{-1}\) units) the energy formula for both species. What values are J and K allowed to assume? What is the degeneracy of the level labeled by a given J and K?
d. Draw a picture of both compounds and show the directions of the three principle axes (a,b,c). On these pictures show the kinf of rotational motion associated with the quantum number K.
e. Given that the electrical transition moment vector \(\vec{\mu}\) connecting species I and II is directed along the Y axis, what are the selection rules J and K?
f. Suppose you are given the photoelectron spectrum of \(CH_2^-\). In this spectrum \(J_j = J_i + 1\) transitions are called R-branch absorptions and those obeying \( J_j = J_i - 1\) are called P-branch transitions , The spacing between lines can increase or decrease as functions of \(J_i\) depending on the changes in the moment of inertia for the transition. If spacings grow closer and closer, we say that the spectrum exhibits a so-called band head formation. In the photoelectron spectrum that you are given, a rotational analysis of the vibrational lines in this spectrum is carried out and it is found that the R-branches show band head formation but the P-branches do not. Based on this information, determine which compound I or II is the \(CH_2^-\) anion. Explain your reasoning.
g. At what J value (of the absorbing species) does the band head occur and at what rotational energy difference?
Q2
Let us consider the vibrational motions of benzene. To consider all of the vibrational modes of benzene we should attach a set of displacement vectors in the x, y, and z directions to each atom in the molecule (giving 36 vectors in all), and evaluate how these transform under the symmetry operations of \(D_{6h}\). For this problem, however, let's only inquire about the C-H stretching vibrations.
a. Represent the C-H stretching motion on each C-H bond by an outward-directed vector on each H atom, designated \(r_i\):
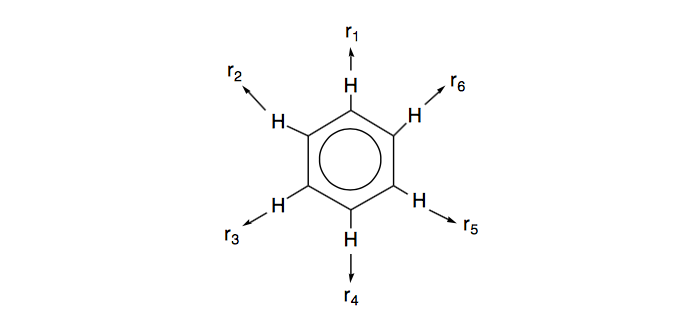
These vectors form the basis for a reducible representation. Evaluate the characters for this reducible representation under the symmetry operations of the \(D_{6h}\) group.
b. Decompose the reducible representation you obtained in part a. into its irreducible components. These are the symmetries of the various C-H stretching vibrational modes in benzene.
c. The vibrational state with zero quanta in each of the vibrational modes (the ground vibrational state) of any molecule always belongs to the totally symmetric representation. For benzene the ground vibrational state is therefore of \(A_{1g}\) symmetry. Am excited state which has one quantum of vibrational excitation in a mode which is of a given symmetry species has the same symmetry species as the mode which is excied (because the vibrational wave functions are given as Hermite polynomials in the stretching coordinate). Thus, for example, excitation (by one quantum) of a vibrational mode of \(A_{2u}\) symmetry gives a wavefunction of \(A_{2u}\) symmetry. To resolve the question of what vibrational modes may be excited by the absorption of infrared radiation we must examine the x, y, and z componenets of the transition dipole integral for initial and final state wave functions \(\psi_i \text{ and } \psi_f\), respectively:
\[ |\langle \psi_f |x| \psi_i \rangle |, |\langle \psi_f |y| \psi_i \rangle |, \text{ and } |\langle \psi_f |z| \psi_i \rangle |. \nonumber \]
Using the information provided above, which of the C-H vibrational modes of benzene will be infrared-active, and how will the transitions be polarized? How many C-H vibrations will you observe in the infrared spectrum of benzene?
d. A vibrational mode will be acrive in Raman spectroscopy only if one of the following integrals is nonzero:
\begin{align} & & &| \langle \psi_f |xy| \psi_i \rangle |, | \langle \psi_f |xz| \psi_i \rangle |, | \langle \psi_f |yz| \psi_i \rangle |, \\ & & &| \langle \psi_f |x^2| \psi_i \rangle |, | \langle \psi_f |y^2| \psi_i \rangle |, \text{ and } | \langle \psi_f |z^2| \psi_i \rangle | . \end{align}
Using the fact that the quadratic operators transform according to the irreducible representations:
\begin{align} \left( x^2 + y^2, z^2 \right) &\Rightarrow && A_{1g} \\ \left( xz, yz \right) &\Rightarrow && E_{1g} \\ \left( x^2 - y^2 ,xy \right) & \Rightarrow && E_{2g} \end{align}
Determine which of the C-H vibrational modes will be Raman-active.
e. Are there any of the C-H stretching vibrational motions of benzene which cannot be observed in either infrared of Raman spectroscopy? Give the irreducible representation label for these unobservable modes.
Q3
In treating the vibrational and rotational motion of a diatomic molecule having reduced mass μ, equilibrium bond length re and harmonic force constant k, we are faced with the following radial Schrödinger equation:
\[ \dfrac{-h^2}{2\mu r^2}\dfrac{d}{dr} \left( r^2 \dfrac{dR}{dr} \right) + \dfrac{J(J + 1)\hbar^2}{2\mu r^2}R + \dfrac{1}{2}k(r-r_e)^2R = ER \nonumber \]
a. Show that the substitution \( R = \dfrac{F}{r}\) leads to:
\[ \dfrac{-h^2}{2\mu}F" + \dfrac{J(J + 1)\hbar^2}{2\mu r^2}F + \dfrac{1}{2}k(r - r_e)^2F = EF \nonumber \]
b. Taking \( r = r_e + \Delta r\text{ and expanding } \dfrac{1}{(1 + x)^2} = 1 - 2x + 3x^2 + ...,\)
show that so-called vibration-rotation coupling term \( \dfrac{J(J + 1)\hbar^2}{2\mu r^2} \) can be approximated (for small \(\Delta \text{ r) by }
\dfrac{J(J + 1)\hbar^2}{2\mu r_e^2} \left( 1 - \dfrac{2\Delta r}{r_e} + \dfrac{3\Delta r^2}{r_e^2} \right).\)
Keep terms only through order \(\Delta r^2.\)
c. Show that, through terms of order \(\Delta r^2\), the above equation for F can be rearranged to yield a new equation of the form:
\[ \dfrac{-\hbar^2}{2\mu} F" + \dfrac{1}{2}\bar{k}( r - \bar{r}_e)^2 F = \left( E - \dfrac{J(J + 1)\hbar^2}{2\mu r_e^2} + \Delta \right) F \nonumber \]
Give explicit expressions for how the modified force constant \(\bar{k} \text{, bond length } \bar{r}_e\), and energy shift \(\Delta\) depend on J, k, \(r_e \text{ and } \mu .\)
d. Given the above modified vibrational problem, we can now conclude that the modified energy levels are:
\[ E = \hbar \sqrt{\dfrac{\bar{k}}{\mu}}\left( v + \dfrac{1}{2}\right) + \dfrac{J(J + 1)\hbar^2}{2\mu r_e^2} - \Delta . \nonumber \]
Explain how the conclusion is "obvious", how for J = 0, k = \(\bar{k} \text{, and }\Delta\) = 0, we obtain the usual harmonic oscillator energy levels. Describe how the energy levels would be expected to vary as J increases from zero and explain how these changes arise from changes in k and \(r_e\). Explain in terms of physical forces involved in the rotating-vibrating molecule why \(r_e\) and k are changed by rotation.


