22.3.4: iv. Review Exercise Solutions
- Page ID
- 81686
Q1
a. For non-degenerate point groups one can simply multiply the representations (since only one representation will be obtained):
\[ a_1 \otimes b_1 = b_1 \nonumber \]
Constructing a "box" in this case is unnecessary since it would only contain a single row. Two unpaired electrons will result in a singlet (S=0, \(M_S\)=0), and three triplets (S=1, \(M_S\)=1, S=1, \(M_S\)=0, S=1, \(M_S=-1\)). The states will be: \(^3B_1(M_S\)=1), \(^3B_1(M_S=0\)), (^3B_1(M_S=-1\)), and \(^1B_1(M_S=0\)).
b. Remember that when coupling non-equivalent linear molecule angular momenta, one simple adds the individual Lz values and vector couples the electron spin. So, in this case \((1\pi_u^12\pi_u^1)\), we have \(M_L\) values of 1+1, 1-1, -1+1, and -1-1 (2,0,0, and -2). The term symbol \(\Delta\) is used to denote the spatially doubly degenerate level \((M_L = \pm 2\)) and there are two distinct spatially non-degenerate levels denote by the term symbol \(\sum (M_L=0).\) Again, two unpaired electrons will result in a singlet (\(S=0 \text{, } M_S=0\)), and three triplets \((S=1\text{, } M_S=1\text{; } S=1 \text{, } M_S=0 \text{; } S=1 \text{, } M_S=-1\)). The states generate are then:
\[ ^1\Delta \text{ }(M_L=2) \text{; one states } (M_S=0), \nonumber \]
\[ ^1\Delta \text{ }(M_L=-2) \text{; one states } (M_S=0), \nonumber \]
\[ ^3\Delta \text{ }(M_L=2) \text{; one states } (M_S=\text{1, 0, and -1),} \nonumber \]
\[ ^3\Delta \text{ }(M_L=-2) \text{; one states } (M_S=\text{1, 0, and -1),} \nonumber \]
\[ ^1\Delta \text{ }(M_L=0) \text{; one states } (M_S=0), \nonumber \]
\[ ^1\Delta \text{ }(M_L=0) \text{; one states } (M_S=0), \nonumber \]
\[ ^3\Delta \text{ }(M_L=0) \text{; one states } (M_S=\text{1, 0, and -1), and } \nonumber \]
\[ ^3\Delta \text{ }(M_L=0) \text{; one states } (M_S=\text{1, 0, and -1)} \nonumber \]
c. Constructing the "box" for two equivalent \(\pi\) electrons one obtains:
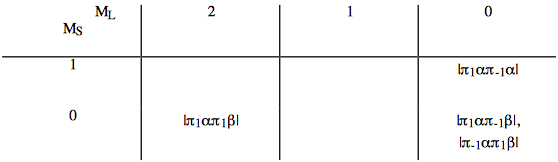
From this "box" one obtains six states:
\[ ^1\Delta (M_L=2)\text{; one state }(M_S=0), \nonumber \]
\[ ^1\Delta (M_L=-2)\text{; one state }(M_S=0), \nonumber \]
\[ ^1\Delta (M_L=0)\text{; one state }(M_S=0), \nonumber \]
\[ ^3\Delta (M_L=0)\text{; three states }(M_S=\text{1, 0, and -1}), \nonumber \]
d. It is not necessary to construct a "box" when coupling non-equivalent angular momenta since the vector coupling results in a range from the sum of the two individual angular momenta to the absolute value of their difference. In this case, \(3d^14d^1\), L=4, 3, 2, 1, 0, and S=1, 0. The term symbol are: \(^3G, ^1G, ^3F, ^1F, ^3D, ^1D, ^3P, ^1P, ^3S\text{, and } ^1S.\) THe L and S angular momenta can be vector coupled to produce further splitting into levels:
\[ \text{ J = L + S ... |L - S|. } \nonumber \]
Denoting J as a term symbol subscript one can identify all the levels and the subsequent (2J + 1) states:
\[ ^3G_5 \text{ (11 states),} \nonumber \]
\[ ^3G_4 \text{ (9 states),} \nonumber \]
\[ ^3G_3 \text{ (7 states),} \nonumber \]
\[ ^1G_4 \text{ (9 states),} \nonumber \]
\[ ^3F_4 \text{ (9 states),} \nonumber \]
\[ ^3F_3 \text{ (7 states),} \nonumber \]
\[ ^3F_2 \text{ (5 states),} \nonumber \]
\[ ^1F_3 \text{ (7 states),} \nonumber \]
\[ ^3D_3 \text{ (7 states),} \nonumber \]
\[ ^3D_2 \text{ (5 states),} \nonumber \]
\[ ^3D_1 \text{ (3 states),} \nonumber \]
\[ ^1D_2 \text{ (5 states),} \nonumber \]
\[ ^3P_2 \text{ (5 states),} \nonumber \]
\[ ^3P_1 \text{ (3 states),} \nonumber \]
\[ ^3P_0 \text{ (1 states),} \nonumber \]
\[ ^1P_1 \text{ (3 states),} \nonumber \]
\[ ^3S_5 \text{ (3 states), and} \nonumber \]
\[ ^1S_0 \text{ (1 states).} \nonumber \]
e. Construction of a "box" for the two equivalent d electrons generates (note the "box" has been turned side ways for convenience):
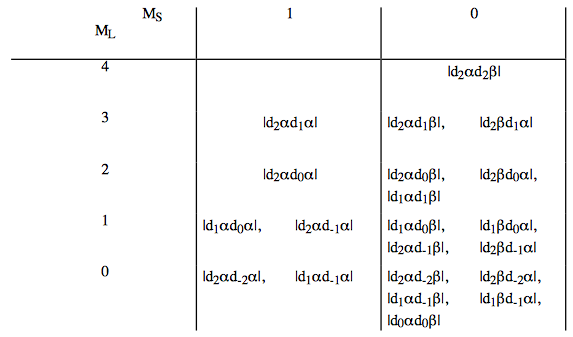
The term symbols are: \(^1G \text{, } ^3F \text{, } ^1D \text{, } ^3P \text{, and } ^1S.\) The L and S angular momenta can be vector coupled to produce further splitting into levels:
\[ ^1G_4 \text{ (9 states),} \nonumber \]
\[ ^3F_4 \text{ (9 states),} \nonumber \]
\[ ^3F_3 \text{ (7 states),} \nonumber \]
\[ ^3F_2 \text{ (5 states),} \nonumber \]
\[ ^1D_2 \text{ (5 states),} \nonumber \]
\[ ^3P_2 \text{ (5 states),} \nonumber \]
\[ ^3P_1 \text{ (3 states),} \nonumber \]
\[ ^3P_0 \text{ (1 states), and} \nonumber \]
\[ ^1S_0 \text{ (1 states).} \nonumber \]


