22.1.5: v. Review Exercise Solutions

Q1

The general relationships are as follows:

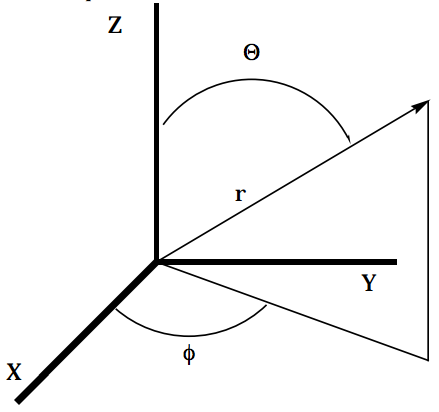
\[ \begin{matrix} x &= \text{rSin} \theta \text{ Cos} \phi &r^2 = x^2 + y^2 + z^2 \\ y &= \text{rSin} \theta \text{ Sin} \phi &\text{Sin} \theta \dfrac{\sqrt{x^2 + y^2}}{\sqrt{x^2 + y^2 + z^2}} \\ z &= \text{rCos} \theta & \text{Cos} \theta = \dfrac{z}{\sqrt{x^2 + y^2 + z^2}} \\ & &\text{Tan} \phi = \dfrac{y}{x} \\ \end{matrix} \nonumber \]

\[ \begin{matrix} a. & \\ & 3x + y - 4z = 12 \\ & 3\text{(rSin} \theta \text{Cos} \phi ) + \text{Sin} \theta \text{Sin} \phi - 4\text{(rCos} \theta ) = 12 \\ & r\text{(3Sin} \theta \text{Cos} \phi + \text{Sin} \theta \text{Sin} \phi - 4\text{Cos} \theta ) = 12 \end{matrix} \nonumber \]
\[ \begin{matrix} b. & \\ & x = \text{rCos} \phi & r^2 = x^2 + y^2 \\ & y = \text{rSin} & \text{Tan} \phi = & \dfrac{y}{x} \\ & z = z & y^2 + z^2 = 9 \\ & &r^2\text{Sin}^2 + z^2 = 9 \end{matrix} \nonumber \]
\[ \begin{matrix} c. \\ & r = 2\text{Sin} \theta \text{Cos} \phi \\ & r = 2 \left( \dfrac{x}{r} \right) \\ & r^2 = 2x \\ & x^2 + y^2 + z^2 = 2x \\ & x^2 -2x + y^2 + z^2 = 0 \\ & x^2 -2x + 1 + y^2 + z^2 = 1 \\ & \left( x -1 \right)^2 + y^2 + z^2 = 1 \end{matrix} \nonumber \]

Q2

a. \[ \begin{matrix} & 9x + 16y\frac{\partial y}{\partial x} = 0 \\ & 16ydy = -9xdx \\ & \dfrac{16}{2}y^2 = -\dfrac{9}{2}x^2 + c \\ & 16y^2 = -9x^2 +c' \\ & \dfrac{y^2}{9} + \dfrac{x^2}{16} = c'' \text{(general equation for an ellipse)} \end{matrix} \nonumber \]


b. \[ \begin{matrix} & 2y + \frac{\partial y}{\partial x} + 6 = 0 \\ & 2y + 6 = -\dfrac{dy}{dx} \\ & -2dx = -\dfrac{dy}{2dx} \\ & -2dx = \dfrac{dy}{y+3} \\ & -2x = ln(y + 3) + c \\ & c'e^{-2x} = y + 3 \\ & y= c'e^{-2x} - 3 \end{matrix} \nonumber \]

Q3

a. First determine the eigenvalues:
\[ \begin{matrix} & \text{det} \begin{bmatrix} &-1 - \lambda & 2 \\ &2 & 2 - \lambda \end{bmatrix} = 0 \\ & (-1 - \lambda )(2 - \lambda ) -2^2 = 0 \\ & -2 + \lambda -2 \lambda + \lambda^2 -4 = 0 \\ & \lambda^2 - \lambda -6 = 0 \\ & ( \lambda -3)( \lambda +2) = 0 \\ & \lambda = 3 \text{ or } \lambda = -2. \end{matrix} \nonumber \]

Next, determine the eigenvectors. First, the eigenvector associated with eigenvalue -2:
\[ \begin{matrix} & \begin{bmatrix} -1 & 2 \\ 2 & 2 \end{bmatrix} \begin{bmatrix} C_{11} \\ C_{21} \end{bmatrix} = -2 \begin{bmatrix} C_{11} \\ C_{21} \end{bmatrix} \\ & -C){11} + 2C_{21} = -2C_{11} \\ & C_{11} = -2C_{21} \end{matrix} \nonumber \]
(Note: The second row offers no new information, e.g. 2\(C_{11} + 2C_{21} = -2C_{21} )\)
\[ \begin{matrix} & C_{11}^2 + C_{21}^2 = 1\text{ (from normalization)} \\ & (-2C_{21})^2 + C_{21}^2 = 1 \\ & 4C_{21}^2 + C_{21}^2 = 1 \\ & 5C_{21}^2 = 1 \\ &C_{21}^2 = 0.2 \\ & C_{21} = \sqrt{0.2} \\ & \text{ (again the second row offers no new information)} \\ & C_{12}^2 + C_{22}^2 = 1 \\ & 0.25C_{22}^2 + C_{22}^2 = 1 \\ & 1.25C_{22}^2 = 1 \\ & C_{22}^2 = 0.8 \\ &C_{22} = \sqrt{0.8} = 2\sqrt{0.2} \text{, and therefore } C_{12} = \sqrt{0.2}. \\ & \text{Therefore the eigenvector matrix becomes:} \\ & \begin{bmatrix} -2\sqrt{0.2} & \sqrt{0.2} \\ \sqrt{0.2} & 2\sqrt{0.2} \end{bmatrix} \end{matrix} \nonumber \]
b. First determine the eigenvalues:
\[ \begin{matrix} & \text{det}\begin{bmatrix} -2 - \lambda & 0 & 0 \\ 0 & -1 - \lambda & 2 \\ 0 & 2 & 2 - \lambda \end{bmatrix} = 0 \\ & \text{det} \left[ -2 - \lambda \right] \text{det} \begin{bmatrix} -1 - \lambda & 2 \\ 2 & 2 - \lambda \end{bmatrix} = 0 \end{matrix} \nonumber \]
From 3a, the solutions then become -2, -2, and 3. Next, determine the eigenvectors. First the eigenvector associated with eigenvalue 3 (the third root):
\[ \begin{bmatrix} -2 & 0 & 0 \\ 0 & -1 & 2 \\ 0 & 2 & 2 \end{bmatrix} \begin{bmatrix} C_{11} \\ C_{21} \\ C_{31} \end{bmatrix} = 3 \begin{bmatrix} C_{11} \\ C_{21} \\ C_{31} \end{bmatrix} \nonumber \]

\[ -2C_{13} = 3C_{13} \text{ (row one)} \\ C_{13} = 0 \\ -C_{23} + 2C_{33} = 3C_{23} \text{ (row two)} \\ 2C_{33} = 2C_{23} \\ C_{33} = 2C_{23} \text{ (again the third row offers no new information)} \\ C_{13}^2 + C_{23}^2 + C_{33}^2 = 1\text{ (from normalization)} \\ 0 + C_{23}^2 + (2C_{23})^2 = 1 \\ 5C_{23}^2 = 1 \\ C_{23} = \sqrt{0.2} \text{, and therefore } C_{33} = \sqrt{0.2} . \nonumber \]

Next, find the pair of eigenvectors associated with the degenerate eigenvalue of -2. First, root one eigenvector one:

\[ -2C_{11} = -2C_{11} \text{ (no new information from row one)} \\ -C_{21} + 2C_{31} = -2C_{21} \text{ (row two)} \\ C_{21} = -2C_{31} \text{ (again the third row offers no new information)} \\ C_{11}^2 + C_{21}^2 + C_{31}^2 = 1 \text{ (from normalization)} \\ C_{11}^2 + (-2C_{31})^2 + C_{31}^2 = 1 \\ C_{11}^2 + 5C_{31}^2 = 1 \\ C_{11} = \sqrt{1 - 5C_{31}^2} \nonumber \]
Note: There are now two equations with three unkowns. Second, root two eigenvector two:
\[ -2C_{12} = -2C_{12} \text{ (no new information from row one)} \\ -C_{21} + 2C_{31} = -2C_{21} \text{ (row two)} \\ C_{21} = -2C_{31} \text{ (again the third row offers no new information)} \\ C_{11}^2 + C_{21}^2 + C_{31}^2 = 1 \text{ (from normalization)} \\ C_{12}^2 + (-2C_{32})^2 + C_{32}^2 = 1 \\ C_{12}^2 + 5C_{32}^2 = 1 \\ C_{12} = \sqrt{1-5C_{32}^2} \nonumber \]
Note: Again there are now two equations with three unknows.
\[ C_{11}C_{12} + C_{21}C_{22} + C_{31}C_{32} = 0 \text{ (from orthogonalization)} \nonumber \]
Now there are five equations with six unknowns.
\[ \text{Arbitrarily choose } C_{11} = 0 \\ C_{11} = 0 = \sqrt{1 - 5C_{31}^2} \\ 5C_{31}^2 = 1 \\ C_{31} = \sqrt{0.2} \\ C_{21} = -2\sqrt{0.2} \\ C_{11}C_{12} + C_{21}C_{22} + C_{31}C_{32} = 0 \text{ (from orthogonalization)} \\ 0 + -2\sqrt{0.2}(-2C_{32}) + \sqrt{0.2} C_{32} = 0 \\ 5C_{32} = 0 \\ C_{32} = 0, C_{22} = 0 \text{, and } C_{12} = 1 \nonumber \]
Therefore the eigenvector matrix becomes:
\[ \begin{bmatrix} 0 & 1 & 0 \\ -2\sqrt{0.2} & 0 & \sqrt{0.2} \\ \sqrt{0.2} & 0 & 2\sqrt{0.2} \end{bmatrix} \nonumber \]

Q4

Show: \( \langle \phi_1 \big| \phi_1 \rangle = 1, \langle \phi_2 \big| \phi_2 \rangle = 1 \text{, and } \langle \phi_1 \big| \phi_2 \rangle = 0\)

\[ \langle \phi_1 | \phi_1 \rangle \overset{?}{=} 1 \\ \left( -2 \sqrt{0.2} \right)^2 + \left( \sqrt{0.2} \right)^2 \overset{?}{=} 1 \\ 4(0.2) + 0.2 \overset{?}{=} 1 \\ 0.8 + 0.2 \overset{?}{=} 1 \\ 1 = 1 \\ \langle \phi_2 \big| \phi_2 \rangle \overset{?}{=} 1 \\ \left( \sqrt{0.2} \right)^2 + \left( 2\sqrt{0.2} \right)^2 \overset{?}{=} 1 \\ 0.2 + 4(0.2) \overset{?}{=} 1 \\ 0.2 + 0.8 \overset{?}{=} 1 \\ 1 = 1 \\ \langle \phi_1\big| _2 \phi \rangle = \langle \phi_2 \big| \phi_1 \rangle \overset{?}{=} 0 \\ -2\sqrt{0.2} \sqrt{0.2} _ \sqrt{0.2}2\sqrt{0.2} \overset{?}{=} 0 \\ -2(0.2) + 2(0.2) \overset{?}{=} 0 \\ -0.4 + 0.4 \overset{?}{=} 0 \\ 0 = 0 \nonumber \]

Q5

Show (for the degenerate eigenvalue; \( \lambda\) = -2): \( \langle \phi_2 \big| \phi_2 \rangle = 1, \langle \phi_2 \big| \phi_2 = 1\text{, and} _1 \big| e \phi \rangle = 0 \)

\[ \langle \phi_1 \big| \phi_1 \rangle \overset{?}{=} 1 \\ 0 + \left( -2\sqrt{0.2} \right)^2 + \left( \sqrt{0.2} \right)^2 \overset{?}{=} 1 \\ 4(0.2) + 0.2 \overset{?}{=} 1 \\ 0.8 + 0.2 \overset{?}{=} 1 \\ 1 = 1 \\ \langle \phi_1 \big| \phi_2 \rangle \overset{?}{=} 1 \\ 1^2 + 0 + 0 \overset{?}{=} 1 \\ 1 = 1 \\ \langle \phi_1 \big| \phi_2 = \langle \phi_2 \big| \phi_1 \rangle \overset{?}{=} 0 \\ (0)(1) + (-2\sqrt{0.2})(0) + (\sqrt{0.2})(0) \overset{?}{=} 0 \nonumber \]

Q6

Suppose the solution is of the form x(t) = eat , with a unknown. Inserting this trial solution into the differential equation results in the following:

\[ \dfrac{d^2}{dt^2}e^{ \alpha t} + k^2 e^{ \alpha t} = 0 \\ \alpha^2e^{ \alpha t} + k^2e^{ \alpha t} = 0 \\ \left( \alpha^2 + k^2 \right) x(t) = 0 \\ \left( \alpha^2 + k^2 \right) = 0 \\ \alpha^2 = -k^2 \\ \alpha = \sqrt{-k^2} \\ \alpha = \pm ik \nonumber \]

\(\therefore\) Solutions are of the form \(e^{-ikt}, e^{ikt},\) or a combination of both: \( x(t) = C_1e^{ikt} + C_2e^{-ikt}. \)
Euler's formula also states that: \( e^{+i\theta} = Cos\Theta \pm iSin\Theta \), so the previous equation for x(t) can also be written as:
\[ x(t) = C_1 \left[ Cos(kt) + iSin(kt) \right] + C_2 \left[ Cos(kt) - iSin(kt) \right] \\ x(t) = \left( C_1 + C_2 \right) Cos(kt) + \left( C_1 + C_2 \right) iSin(kt)\text{, or alternatively} \\ x(t) = C_3Cos(kt) + C_4Sin(kt). \nonumber \]

We can determin these coefficients by making use of the "boundary conditions".

\[ \text{at t } = 0, x(0) = L \\ x(0) = C_3Cos(0) + C_4Sin(0) = L \\ C_3 = L \\ \text{at t } = 0, \dfrac{dx(0)}{dt}=0 \\ \dfrac{d}{dt}x(t) = \dfrac{d}{dt} \left( C_3Cos(kt) + C_4Sin(kt) \right) \\ \dfrac{d}{dt}x(t) = -C_3kSin(kt) + C_4kCos(kt) \\ \dfrac{d}{dt}x(0) = 0 = -C_3kSin(0) + C_4kCos(0) \\ C_4k = 0 \\ C_4 = 0 \nonumber \]
\(\therefore\) The solution is of the form: \( x(t) = LCos(kt) \)