22.1.1: i. Review Exercises

Last updated
Save as PDF

Page ID: 74207

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Q1

Transform (using the coordinate system provided below) the following functions accordingly:

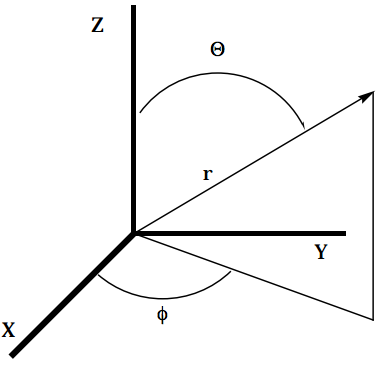
Screen Shot 2017-01-04 at 9.33.49 AM.png

a. from Cartesian to spherical polar coordinates

\[ 3x + y -4z =12 \nonumber \]

b. from Cartesian to cylindrical coordinates

\[ y^2 + z^2 = 9 \nonumber \]

c. from spherical polar to Cartesian coordinates

\[ r = 2\sin \theta \cos \phi \nonumber \]

Q2

Perform a separation of variables and indicate the general solution for the following expressions:

a. \( 9x + 16y \dfrac{\partial y}{\partial x} = 0 \)

b. \( 2y + \dfrac{\partial y}{\partial x} + 6 = 0 \)

Q3

Find the eigenvalues and corresponding eigenvectors of the following matrices:

\( \begin{bmatrix} -1 & 2 \\ 2 & 2 \end{bmatrix} \)
\( \begin{bmatrix} -2 & 0 & 0 \\ 0 & -1 & 2 \\ 0 & 2 & 2 \end{bmatrix} \)

Q4

For the hermitian matrix in review exercise 3a show that the eigenfunctions can be normalized and that they are orthogonal.

Q5

For the hermitian matrix in review exercise 3b show that the pair of degenerate eigenvalues can be made to have orthonormal eigenfunctions.

Q6

Solve the following second order linear differential equation subject to the specified "boundary conditions":

\[ \dfrac{d^2 x}{dt^2} + k^2x(t) = 0 \nonumber \]

where \(x(t=0) = L\) and \(\dfrac{dx}{dt} \bigg|_{t=0} = 0. \)