18.4: Atomic Orbital Basis Sets

The basis orbitals commonly used in the LCAO-MO-SCF process fall into two classes Slater-type orbitals and Cartesian Gaussian-type orbitals.

Slater-type orbitals (STO) are characterized by quantum numbers \(n\), \(l\), and \(m\) and exponents (which characterize the 'size' of the basis function) \(\xi\):

\[ \chi_{n,l,m}(r,\theta ,\phi )= N_{n,l,m,\xi} Y_{l,m}(\theta ,\phi )r^{n-1}e^{-\xi r}, \nonumber \]

and \(N_{n,l,m, \xi}\) denotes the normalization constant.

Cartesian Gaussian-type orbitals (GTO) are characterized by quantum numbers \(a\), \(b\), and \(c\) which detail the angular shape and direction of the orbital and exponents \(\alpha\) which govern the radial 'size' of the basis function akin to \(\xi\) in STOs.

\[ \chi_{a,b,c}(r, \theta ,\phi )- N'_{a,b,c,\alpha}\textbf{x}^a\textbf{y}^b\textbf{z}^ce^{-\alpha r^2}, \nonumber \]

For example, orbitals with \(a\), \(b\), and \(c\) values of 1,0,0 or 0,1,0 or 0,0,1 are \(p_x\), \(p_y\), and \(p_z\) orbitals; those with \(a\), \(b\), and \(c\) values of 2, 0, 0 or 0, 2, 0 or 0, 0, 2 and 1, 1, 0 or 0, 1, 1 or 1, 0, 1 span the space of five d orbitals and one s orbital (the sum of the 2, 0, 0 and 0, 2, 0 and 0, 0, 2 orbitals is an s orbital because \(x^2 + y^2 + z^2 = r^2\) is independent of \(\theta \text{ and } \phi \)).

For both types of orbitals, the coordinates \(r\, \theta, \text{ and } \phi\) refer to the position of the electron relative to a set of axes attached to the center on which the basis orbital is located.

The Utility of Gaussians

Although STOs are preferred on fundamental grounds (e.g., as demonstrated in Appendices A and B, the hydrogen atom orbitals are of this form and the exact solution of the many-electron Schrödinger equation can be shown to be of this form (in each of its coordinates) near the nuclear centers), STOs are used primarily for atomic and linear-molecule calculations because the multi-center integrals \( \langle \chi_a \chi_b \big| g \big| \chi_e \chi_d \rangle \) (each basis orbital can be on a separate atomic center) which arise in polyatomic-molecule calculations can not efficiently be performed when STOs are employed. In contrast, such integrals can routinely be done when GTOs are used. This fundamental advantage of GTOs has lead to the dominance of these functions in molecular quantum chemistry.

To understand why integrals over GTOs can be carried out when analogous STO based integrals are much more difficult, one must only consider the orbital products ( \( \chi_a \chi_c (r_1) \text{ and } \chi_b \chi_d (r_2) \) ) which arise in such integrals. For orbitals of the GTO form, such products involve \( e^{-\alpha_a (\textbf{r}-\textbf{R}_a)^2}e^{-\alpha_c( \textbf{r}-\textbf{R}_c )^2} \). By completing the square in the exponent, this product can be rewritten as follows:

\[ e^{-\alpha_a (\textbf{r}-\textbf{R}_a)^2} e^{-\alpha_c (\textbf{r}-\textbf{R}_c)^2} = e^{-(\alpha_a + \alpha_c )(\textbf{r}-\textbf{R'})^2}e^{-\alpha ' (\textbf{R}_a-\textbf{R}_c)^2}, \nonumber \]

where

\[ \textbf{R}' = \dfrac{\alpha_a\textbf{R}_a + \alpha_c\textbf{R}_c}{\alpha_a + \alpha_c} \nonumber \]

and

\[ \alpha ' = \dfrac{\alpha_a \alpha_c}{\alpha_a + \alpha_c}. \nonumber \]

Thus, the product of two GTOs on different centers is equal to a single other GTO at a center \(\textbf{R}'\) between the two original centers. As a result, even a four-center two-electron integral over GTOs can be written as, at most, a two-center two-electron integral; it turns out that this reduction in centers is enough to allow all such integrals to be carried out. A similar reduction does not arise for STOs because the product of two STOs can not be rewritten as a new STO at a new center.

To overcome the primary weakness of GTO functions, that they have incorrect behavior near the nuclear centers (i.e., their radial derivatives vanish at the nucleus whereas the derivatives of STOs are non-zero), it is common to combine two, three, or more GTOs, with combination coefficients which are fixed and not treated as LCAO-MO parameters, into new functions called contracted GTOs or CGTOs. Typically, a series of tight, medium, and loose GTOs (i.e., GTOs with large, medium, and small \(\alpha\) values, respectively) are multiplied by so-called contraction coefficients and summed to produce a CGTO which appears to possess the proper 'cusp' (i.e., non-zero slope) at the nuclear center (although even such a combination can not because each GTO has zero slope at the nucleus).

Basis Set Libraries

Much effort has been devoted to developing sets of STO or GTO basis orbitals for main-group elements and the lighter transition metals. This ongoing effort is aimed at providing standard basis set libraries which:

1. Yield reasonable chemical accuracy in the resultant wavefunctions and energies.
2. Are cost effective in that their use in practical calculations is feasible.
3. Are relatively transferrable in the sense that the basis for a given atom is flexible enough to be used for that atom in a variety of bonding environments (where the atom's hybridization and local polarity may vary).

The Fundamental Core and Valence Basis

In constructing an atomic orbital basis to use in a particular calculation, one must choose from among several classes of functions. First, the size and nature of the primary core and valence basis must be specified. Within this category, the following choices are common:

1. A minimal basis in which the number of STO or CGTO orbitals is equal to the number of core and valence atomic orbitals in the atom.
2. A double-zeta (DZ) basis in which twice as many STOs or CGTOs are used as there are core and valence atomic orbitals. The use of more basis functions is motivated by a desire to provide additional variational flexibility to the LCAO-MO process. This flexibility allows the LCAO-MO process to generate molecular orbitals of variable diffuseness as the local electronegativity of the atom varies. Typically, double-zeta bases include pairs of functions with one member of each pair having a smaller exponent (\(\zeta \text{ or } \alpha\) value) than in the minimal basis and the other member having a larger exponent.
3. A triple-zeta (TZ) basis in which three times as many STOs or CGTOs are used as the number of core and valence atomic orbitals.
4. Dunning has developed CGTO bases which range from approximately DZ to substantially beyond TZ quality (T. H. Dunning, J. Chem. Phys. 53 , 2823 (1970); T. H. Dunning and P. J. Hay in Methods of Electronic Structure Theory, H. F. Schaefer, III Ed., Plenum Press, New York (1977))). These bases involve contractions of primitive GTO bases which Huzinaga had earlier optimized (S. Huzinaga, J. Chem. Phys. 42 , 1293 (1965)) for use as uncontracted functions (i.e., for which Huzinaga varied the \(\alpha\) values to minimize the energies of several electronic states of the corresponding atom). These Dunning bases are commonly denoted, for example, as follows for first-row atoms: (10s,6p/5s,4p), which means that 10 s-type primitive GTOs have been contracted to produce 5 separate s-type CGTOs and that 6 primitive p-type GTOs were contracted to generate 4 separate p-type CGTOs. More recent basis sets from the Dunning group are given in T. Dunning, J. Chem. Phys. 90 , 1007 (1990).
5. Even-tempered basis sets (M. W. Schmidt and K. Ruedenberg, J. Chem. Phys. 71 , 3961 (1979)) consist of GTOs in which the orbital exponents ak belonging to series of orbitals consist of geometrical progressions: \(\alpha_k \text{ = a } \beta_k\), where \(\alpha\) and \(\beta\) characterize the particular set of GTOs.
6. STO-3G bases were employed some years ago (W. J. Hehre, R. F. Stewart, and J. A. Pople, J. Chem. Phys. 51 , 2657 (1969)) but are less popular recently. These bases are constructed by least squares fitting GTOs to STOs which have been optimized for various electronic states of the atom. When three GTOs are employed to fit each STO, a STO-3G basis is formed.
7. 4-31G, 5-31G, and 6-31G bases (R. Ditchfield, W. J. Hehre, and J. A. Pople, J. Chem. Phys. 54 , 724 (1971); W. J. Hehre, R. Ditchfield, and J. A. Pople, J. Chem. Phys. 56 , 2257 (1972); P. C. Hariharan and J. A. Pople, Theoret. Chim. Acta. (Berl.) 28 , 213 (1973); R. Krishnan, J. S. Binkley, R. Seeger, and J. A. Pople, J. Chem. Phys. 72 , 650 (1980)) employ a single CGTO of contraction length 4, 5, or 6 to describe the core orbital. The valence space is described at the DZ level with the first CGTO constructed from 3 primitive GTOs and the second CGTO built from a single primitive GTO.

The values of the orbital exponents (\(\zeta s \text{ or } \alpha s\)) and the GTO-to-CGTO contraction coefficients needed to implement a particular basis of the kind described above have been tabulated in several journal articles and in computer data bases (in particular, in the data base contained in the book Handbook of Gaussian Basis Sets: A. Compendium for Ab initio Molecular Orbital Calculations , R. Poirer, R. Kari, and I. G. Csizmadia, Elsevier Science Publishing Co., Inc., New York, New York (1985)).

Several other sources of basis sets for particular atoms are listed in the Table shown below (here JCP and JACS are abbreviations for the Journal of Chemical Physics and the Journal of The American Chemical Society, respectively).

Literature Reference	Basis Type	Atoms
Hehre, W.J.; Stewart, R.F.; Pople, J.A. JCP 51 , 2657 (1969). Hehre, W.J.; Ditchfield, R.; Stewart, R.F.; Pople, J.A. JCP 52 , 2769 (1970).	STO - 3G	H-Ar
Binkley, J.S.; Pople, J.A.; Hehre, W.J. JACS 102 , 939 (1980).	3-21G	H-Ne
Gordon, M.S.; Binkley, J.S.; Pople, J.A.; Pietro, W.J.; Hehre, W.J. JACS 104 , 2797 (1982).	3-21G	Na-Ar
Dobbs, K.D.; Hehre, W.J., J. Comput. Chem. 7 , 359 (1986).	3-21G	K, Ca, Ga
Dobbs, K.D.; Hehre, W.J., J. Comput. Chem. 8, 880 (1987).	3-21G	Sc-Zn
Ditchfield, R.; Hehre, W.J.; Pople, J.A., JCP 54 , 724 (1971).	6-31G	H
Dill, J.D.; Pople, J.A., JCP 62 , 2921 (1975).	6-31G	Li, B
Binkley, J.S.; Pople, J.A., JCP 66 , 879 (1977)	6-31G	Be
Hehre, W.J.; Ditchfield, R.; Pople, J.A., JCP 56 , 2257 (1972).	6-31G	C-F
Francl, M.M.; Pietro, W.J.; Hehre, W.J.; Binkley, J.S.; Gordon, M.S.; DeFrees, D.J.; Pople, J.A. JCP 77 , 3654 (1982).	6-31G	Na-Ar
Dunning, T. JCP 53 , 2823 (1970).	(4s/2s) (4s/3s) (9s5p/3s2p) (9s5p/4s2p) (9s5p/5s3p)	H H B-F B-F B-F
Dunning, T. JCP 55 , 716 (1971).	(5s/3s) (10s/4s) (10s/5s) (10s6p/5s3p) (10s6p/5s4p)	H Li Be B-Ne B-Ne
Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. JCP 72 , 650 (1980).	6-311G	H-Ne
Dunning, unpublished VDZ.	(4s/2s) (9s5p/3s2) (12s8p/4s3p)	H Li, Be, C-Ne Na-Ar
Dunning, unpublished VTZ.	(5s/3s) (6s/3s) (12s6p/4s3p) (17s10p/5s4p)	H H Li, Be, C-Ne Mg-Ar
Dunning, unpublished VQZ.	(7s/4s) (8s/4s) (16s7p/5s4p)	H H B-Ne
Dunning, T. JCP 90 , 1007 (1989). (pVDZ,pVTZ,pVQZ correlation-consistent)	(4s1p/2s1p) (5s2p1d/3s2p1d) (6s3p1d1f/4s3p2d1f) (9s4p1d/3s2p1d) (10s5p2d1f/4s3p2d1f) (12s6p3d2f1g/5s4p3d2f1g)	H H H B-Ne B-Ne B-Ne
Huzinaga, S.; Klobukowski, M.; Tatewaki, H. Can. J. Chem. 63 , 1812 (1985).	(14s/2s) (14s9p/2s1p) (16s9p/3s1p) (16s11p/3s2p)	Li, Be B-Ne Na-Mg Al-Ar
Huzinaga, S.; Klobukowski, M. THEOCHEM. 44 , 1 (1988).	(14s10p/2s1p) (17s10p/3s1p) (17s13p/3s2p) (20s13p/4s2p) (20s13p10d/4s2p1d) (20s14p9d/4s3d1d)	B-Ne Na-Mg Al-Ar K-Ca Sc-Zn Ga
McLean, A.D.; Chandler, G.S. JCP 72 , 5639 (1980).	(12s8p/4s2p) (12s8p/5s2p) (12s8p/6s4p) (12s9p/6s4p) (12s9p/6s5p)	Na-Ar, P\(^-\), S\(^-\), Cl\(^-\) Na-Ar, P\(^-\), S\(^-\), Cl\(^-\) Na-Ar, P\(^-\), S\(^-\), Cl\(^-\) Na-Ar, P\(^-\), S\(^-\), Cl\(^-\) Na-Ar, P\(^-\), S\(^-\), Cl\(^-\)
Dunning, T.H.Jr.; Hay, P.J. Chapter 1 in 'Methods of Electronic Structure Theory', Schaefer, H.F.III, Ed., Plenum Press, N.Y., 1977.	(11s7p/6s4p)	Al-Cl
Hood, D.M.; Pitzer, R.M.; Schaefer, H.F.III, JCP 71 , 705 (1979).	(14s11p6d/10s8p3d)	Sc-Zn
Schmidt, M.W.; Ruedenberg, K. JCP 71 , 3951 (1979). (regular even-tempered)	([N]s), N=3-10 ([2N]s), N=3-10 ([2N]s), N=3-14 ([2N]s[N]p), N=3-11 ([2N]s[N]p), N=3-13 ([2N]s[N]p), N=4-12 ([2N-6]s[N]p), N=7-15	H He Li, Be B, N-Ne C Na, Mg Al-Ar

Polarization Functions

In addition to the fundamental core and valence basis described above, one usually adds a set of so-called polarization functions to the basis. Polarization functions are functions of one higher angular momentum than appears in the atom's valence orbital space (e.g, d-functions for C, N , and O and p-functions for H). These polarization functions have exponents (\(\zeta \text{ or } \alpha\)) which cause their radial sizes to be similar to the sizes of the primary valence orbitals ( i.e., the polarization p orbitals of the H atom are similar in size to the 1s orbital). Thus, they are not orbitals which provide a description of the atom's valence orbital with one higher l-value; such higher-l valence orbitals would be radially more diffuse and would therefore require the use of STOs or GTOs with smaller exponents.

The primary purpose of polarization functions is to give additional angular flexibility to the LCAO-MO process in forming the valence molecular orbitals. This is illustrated below where polarization d\(_\pi\) orbitals are seen to contribute to formation of the bonding \(\pi \) orbital of a carbonyl group by allowing polarization of the Carbon atom's p\(_\pi\) orbital toward the right and of the Oxygen atom's p\(_\pi\) orbital toward the left.

Figure 18.4.1: Insert caption here!

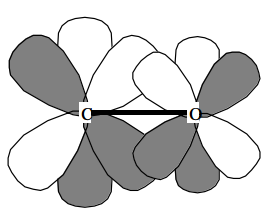
Polarization functions are essential in strained ring compounds because they provide the angular flexibility needed to direct the electron density into regions between bonded atoms.

Functions with higher l-values and with 'sizes' more in line with those of the lower-l orbitals are also used to introduce additional angular correlation into the calculation by permitting polarized orbital pairs (see Chapter 10) involving higher angular correlations to be formed. Optimal polarization functions for first and second row atoms have been tabulated (B. Roos and P. Siegbahn, Theoret. Chim. Acta (Berl.) 17 , 199 (1970); M. J. Frisch, J. A. Pople, and J. S. Binkley, J. Chem. Phys. 80, 3265 (1984)).

Diffuse Functions

When dealing with anions or Rydberg states, one must augment the above basis sets by adding so-called diffuse basis orbitals. The conventional valence and polarization functions described above do not provide enough radial flexibility to adequately describe either of these cases. Energy-optimized diffuse functions appropriate to anions of most lighter main group elements have been tabulated in the literature (an excellent source of Gaussian basis set information is provided in Handbook of Gaussian Basis Sets , R. Poirier, R. Kari, and I. G. Csizmadia, Elsevier, Amsterdam (1985)) and in data bases. Rydberg diffuse basis sets are usually created by adding to conventional valence-pluspolarization bases sequences of primitive GTOs whose exponents are smaller than that (call it \(\alpha_{\text{diff}}\)) of the most diffuse GTO which contributes strongly to the valence CGTOs. As a 'rule of thumb', one can generate a series of such diffuse orbitals which are liniarly independent yet span considerably different regions of radial space by introducing primitive GTOs whose exponents are \( \frac{1}{3}\alpha_{\text{diff}}, \frac{1}{9}\alpha_{\text{diff}}, \frac{1}{27}\alpha_{\text{diff}}, \) etc.

Once one has specified an atomic orbital basis for each atom in the molecule, the LCAO-MO procedure can be used to determine the \(C_{\nu ,i}\) coefficients that describe the occupied and virtual orbitals in terms of the chosen basis set. It is important to keep in mind that the basis orbitals are not themselves the true orbitals of the isolated atoms; even the proper atomic orbitals are combinations (with atomic values for the \(C_{\nu ,i}\) coefficients) of the basis functions. For example, in a minimal-basis-level treatment of the Carbon atom, the 2s atomic orbital is formed by combining, with opposite sign to achieve the radial node, the two CGTOs (or STOs); the more diffuse s-type basis function will have a larger \(C_{i,\nu}\) coefficient in the 2s atomic orbital. The 1s atomic orbital is formed by combining the same two CGTOs but with the same sign and with the less diffuse basis function having a larger \(C_{\nu ,i}\) coefficient. The LCAO-MO-SCF process itself determines the magnitudes and signs of the \(C_{\nu ,i}\).