15.1: Rotational Transitions
- Page ID
- 60586
Within the approximation that the electronic, vibrational, and rotational states of a molecule can be treated as independent, the total molecular wavefunction of the "initial" state is a product
\[ \Phi_i = \psi_{ei} \chi_{vi} \phi_{ri} \nonumber \]
of an electronic function \(\psi_{ei}, \text{ a vibrational function } \chi_{vi}, \text{ and a rotational function } \phi_{ri}. \text{ A similar product expression holds for the "final" wavefunction } \Phi_f.\)
In microwave spectroscopy, the energy of the radiation lies in the range of fractions of a \(cm^{-1} \text{ through several } cm^{-1}\); such energies are adequate to excite rotational motions of molecules but are not high enough to excite any but the weakest vibrations (e.g., those of weakly bound Van der Waals complexes). In rotational transitions, the electronic and vibrational states are thus left unchanged by the excitation process; hence \(\psi_{ei} = \psi_{ef} \text{ and } \chi_{vi} = \chi_{vf}.\)
Applying the first-order electric dipole transition rate expressions
\[ R_{i,f} = 2\pi g(\omega_{f,i}) |\alpha_{f,i}|^2 \nonumber \]
obtained in Chapter 14 to this case requires that the E1 approximation
\[ R_{i,f} = \left( \dfrac{2\pi}{\hbar^2} \right) g(\omega_{f,i}) | \textbf{E}_0\cdot{\langle}\Phi_f |\mu | \Phi_i \rangle |^2 \nonumber \]
be examined in further detail. Specifically, the electric dipole matrix elements \( \langle \Phi_f | \mu | \Phi_i \rangle \text{ with } \mu = \sum\limits_j e \textbf{r}_j + \sum\limits_a Z_a e \textbf{R}_a \) must be analyzed for \(\Phi_i \text{ and } \Phi_f\) being of the product form shown above.
The integrations over the electronic coordinates contained in \( \langle \Phi_f |\mu |\Phi_i \rangle ,\) as well as the integrations over vibrational degrees of freedom yield "expectation values" of the electric dipole moment operator because the electronic and vibrational components of \( \Phi_i \text{ and } \Phi_f\) are identical:
\[ \langle \psi_{ei}| \mu | \psi_{ei} \rangle = \mu(\textbf{R}) \nonumber \]
is the dipole moment of the initial electronic state (which is a function of the internal geometrical degrees of freedom of the molecule, denoted R); and
\[ \langle \chi_{vi} | \mu (\textbf{R} ) |\chi_{vi} \rangle = \mu_{ave} \nonumber \]
is the vibrationally averaged dipole moment for the particular vibrational state labeled \(\chi_{vi}. \text{ The vector } \mu_{ave}\) mave has components along various directions and can be viewed as a vector "locked" to the molecule's internal coordinate axis (labeled a, b, c as below).
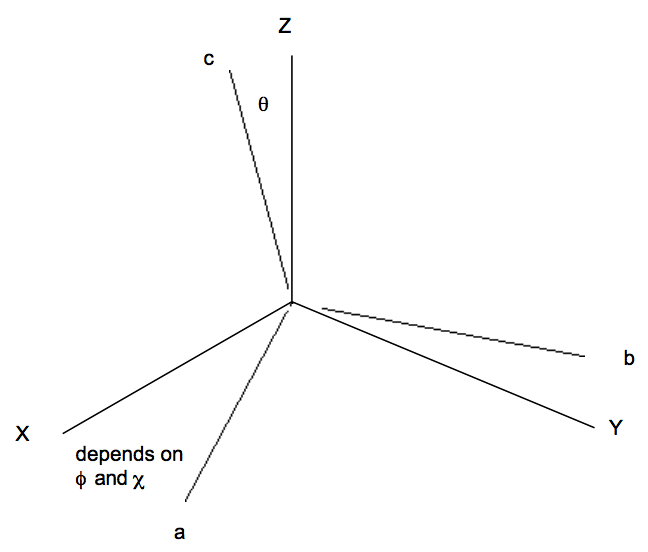
The rotational part of the \( \langle \Phi_f | \mu | \Phi_i \rangle \)integral is not of the expectation value form because the initial rotational function \(\phi_{ir} \text{ is not the same as the final } \phi_{fr}\). This integral has the form:
\[ \langle \Phi_{ir} | \mu_{ave} | \Phi_{fr} \rangle = \int (Y^{\text{*}}_{L,M}(\theta,\phi)) \mu_{ave} Y_{\text{L', M'}}(\theta, \phi) \text{ sin}\theta \text{ d}\theta \text{ d}\phi \nonumber \]
or linear molecules whose initial and final rotational wavefunctions are \(Y_{\text{L,M}} \text{ and } Y_{\text{L',M'}} \), respectively, and
\[ \langle \phi_{ir} | \mu_{ave} | \phi_{fr} \rangle = \sqrt{\dfrac{2L + 1}{8\pi^2}}\sqrt{\dfrac{2L' + 1}{8\pi^2}} \nonumber \]
\[ \int \left( D_{\text{L, M, K}}(\theta , \phi , \chi) \mu_{ave} D^{\text{*}}_{\text{L', M', K'}}(\theta , \phi , \chi) \text{ sin}\theta \text{ d}\theta \text{ d}\phi \text{ d}\chi \right) \nonumber \]
for spherical or symmetric top molecules (here, \( \sqrt{\dfrac{2L + 1}{8\pi^2}}D^{\text{*}}_{\text{L, M, K}}(\theta , \phi , \chi) \) are the normalized rotational wavefunctions described in Chapter 13 and in Appendix G). The angles \(\theta , \phi , \text{ and } \chi\) refer to how the molecule-fixed coordinate system is oriented with respect to the space-fixed X, Y, Z axis system.
Linear Molecules
For linear molecules, the vibrationally averaged dipole moment \(\mu_{ave}\) lies along the molecular axis; hence its orientation in the lab-fixed coordinate system can be specified in terms of the same angles \((\theta \text{ and } \phi)\) that are used to describe the rotational functions \(Y_{\text{L,M}} (\theta ,\phi ).\) Therefore, the three components of the \( \langle \phi_{ir} | \mu_{ave} | \phi_{fr} \rangle\) integral can be written as:
\[ \langle \phi_{ir} | \mu_{ave} | \phi_{fr} \rangle_x = \mu \int Y^{\text{*}}_{\text{L, M}}(\theta ,\phi) \text{ sin}\theta \text{ cos}\phi \text{ Y}_{\text{L', M'}}(\theta , \phi )\text{ sin}\theta \text{ d}\theta \text{ d}\phi \nonumber \]
\[ \langle \phi_{ir} | \mu_{ave} | \phi_{fr} \rangle_y = \mu \int Y^{\text{*}}_{\text{L, M}}(\theta ,\phi) \text{ sin}\theta \text{ cos}\phi \text{ Y}_{\text{L', M'}}(\theta , \phi )\text{ sin}\theta \text{ d}\theta \text{ d}\phi \nonumber \]
\[ \langle \phi_{ir} | \mu_{ave} | \phi_{fr} \rangle_z = \mu \int Y^{\text{*}}_{\text{L, M}}(\theta ,\phi) \text{ sin}\theta \text{ cos}\phi \text{ Y}_{\text{L', M'}}(\theta , \phi )\text{ sin}\theta \text{ d}\theta \text{ d}\phi \nonumber \]
where \(\mu\) is the magnitude of the averaged dipole moment. If the molecule has no dipole moment, all of the above electric dipole integrals vanish and the intensity of E1 rotational transitions is zero.
The three E1 integrals can be further analyzed by noting that cos\( \theta \propto \text{ Y}_{\text{1,0}}; \text{ sin}\theta \text{ cos}\phi \propto \text{ Y}_{\text{1,1}} + \text{ Y}_{\text{1,-1}}; \text{ and sin}\theta \text{ sin}\phi \propto \text{ Y}_{\text{1,1}} - \text{ Y}_{\text{1,-1}}\) and using the angular momentum coupling methods illustrated in Appendix G. In particular, the result given in that appendix:
\[ D_{\text{j, m, m'}}D_{\text{l, n, n'}} = \sum\limits_{\text{J, M, M'}}\langle J,M|j,m; l,n\rangle \langle j,m'; l,n'|J,M' \rangle D_{\text{J, M, M'}} \nonumber \]
when multiplied by D\(^{\text{*}}_{\text{J, M, M'}} \text{ and integrated over sin}\theta \text{ d}\theta \text{ d}\phi \text{ d}\chi\), yields:
\[ \int D^{\text{*}}_{\text{J, M, M'}} D_{\text{j, m, m'}}D_{\text{l, n, n'}} \text{ sin}\theta\text{ d}\theta \text{ d}\phi \text{ d}\chi \nonumber \]
\[ = \dfrac{8\pi^2}{2J+1}\langle \text{ J,M| j,m ; l,n }\rangle \langle \text{ j,m' ; l,n'|J, M' } \rangle \nonumber \]
\[ = 8\pi^2 \left( \dfrac{jlJ}{mn-M} \right) \left( \dfrac{jlJ}{m'n'-M'} \right) \left( -1 \right)^{\text{M+M'}}. \nonumber \]
To use this result in the present linear-molecule case, we note that the \(D_{\text{J,M,K}} \text{ functions and the Y}_{\text{J,M}}\) functions are related by:
\[ \text{Y}_{\text{J,M}}(\theta ,\phi ) = \sqrt{\dfrac{2J + 1}{4\pi}} D^{\text{*}}_{\text{J, M, 0}}(\theta ,\phi ,\chi). \nonumber \]
The normalization factor is now \( \sqrt{\frac{2J + 1}{4\pi}} \text{ rather than} \sqrt{\frac{2J + 1}{8\pi^2}}\) because the \(\text{Y}_{\text{J,M}}\) are no longer functions of \(\chi\), and thus the need to integrate over \( 0 \leq \chi \leq 1\pi\) disappears. Likewise, the \(\chi \text{-dependence of}\) \(\text{D}^{\text{*}}_{\text{J,M,K}}\) disappears for K = 0.
We now use these identities in the three E1 integrals of the form
\[ \mu \int Y^{\text{*}}_{\text{L,M}}(\theta ,\phi) Y_{\text{1,m}}(\theta , \phi) Y_{\text{L',M'}}(\theta ,\phi)\text{ sin}\theta \text{ d}\theta \text{ d}\phi , \nonumber \]
with m = 0 being the Z- axis integral, and the Y- and X- axis integrals being combinations of the m = 1 and m = -1 results. Doing so yields:
\[ \mu \int Y^{\text{*}}_{\text{L,M}}(\theta , \phi) Y_{\text{1,m}}(\theta ,\phi )\text{ Y}_{\text{L', M'}}(\theta ,\phi) \text{ sin}\theta \theta{ d}\theta \text{ d}\phi \nonumber \]
\[ =\mu \sqrt{\dfrac{2L + 1}{4\pi} \dfrac{2L' + 1}{4\pi} \dfrac{3}{4\pi}}\int D_{\text{L, M, 0}}\textbf{ D}^{\text{*}}_{\text{l, m, 0}}\textbf{D}^{\text{*}}_{\text{L', M', 0}} \text{ sin}\theta \text{ d}\theta \text{ d}\phi \text{ d}\dfrac{\chi}{2\pi}. \nonumber \]
The last factor of \(1/2\pi\) is inserted to cancel out the integration over \(d\chi \)that, because all K-factors in the rotation matrices equal zero, trivially yields \(2\pi \). Now, using the result shown above expressing the integral over three rotation matrices, these E1 integrals for the linearmolecule case reduce to:
\[ \mu \int\text{ Y}^{\text{*}}_{\text{L,M}}(\theta , \phi)\text{ Y}_{\text{1,m}}(\theta ,\phi)\text{ Y}_{\text{L',M'}}(\theta ,\phi)\text{ sin}\theta \text{ d}\theta \text{ d}\phi \nonumber \]
\[ = \mu \sqrt{\dfrac{2L + 1}{4\pi}\dfrac{2L' + 1}{4\pi}\dfrac{3}{4\pi}}\dfrac{8\pi^2}{2\pi}\left( \dfrac{L' 1 L}{M'm-M} \right)\left( \dfrac{L' 1 L}{0 0 -0} \right)(-1)^M \nonumber \]
\[ \mu\sqrt{(2L + 1)(2L' + 1)\dfrac{3}{4\pi}}\left( \dfrac{L' 1 L}{M' m -M} \right) \left( \dfrac{L' 1 L}{0 0 -0} \right) (-1)^M. \nonumber \]
Applied to the z-axis integral (identifying m = 0), this result therefore vanishes unless:
\[ \text{M} = \text{M'} \nonumber \]
and
\[ \text{L} = \text{L'} + 1 \text{ or L' }- 1. \nonumber \]
Even though angular momentum coupling considerations would allow L = L' (because coupling two angular momenta with j = 1 and j = L' should give L'+1, L', and L'-1), the 3-j symbol \( \left( \dfrac{\text{L' 1 L}}{\text{0 0 -0}} \right) \) vanishes for the L = L' case since 3-j symbols have the following symmetry
\[ \left( \dfrac{\text{L' 1 L}}{\text{M' m -M}} \right) = (-1)^{\text{L+L'+1}} \left( \dfrac{\text{L' 1 L}}{\text{-M' -m M}} \right) \nonumber \]
with respect to the M, M', and m indices. Applied to the \( \left( \dfrac{\text{L' 1 L}}{\text{0 0 -0}} \right) \) 3-j symbol, this means that this particular 3-j element vanishes for L = L' since L + L' + 1 is odd and hence \((-1)^{\text{L + L' + 1}}\) is -1.
Applied to the x- and y- axis integrals, which contain m = ± 1 components, this same analysis yields:
\[ \mu \sqrt{\text{(2L + 1)(2L' + 1)}\dfrac{3}{4\pi}}\left( \dfrac{\text{L' 1 L}}{M' \pm 1 -M} \right) \left( \dfrac{\text{L' 1 L}}{\text{0 0 -0}} \right) (-1)^M \nonumber \]
which then requires that
\[ \text{M} = \text{M'} \pm 1 \nonumber \]
and
\[ \text{L} = \text{ L' + 1, L' -1} \nonumber \]
with L = L' again being forbidden because of the second 3-j symbol.
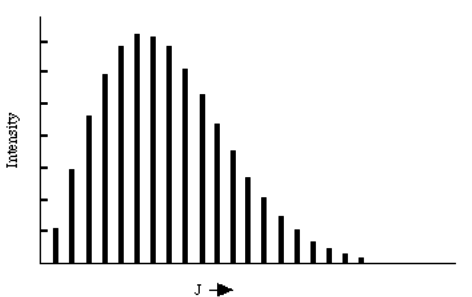
These results provide so-called "selection rules" because the limit the L and M values of the final rotational state, given the L', M' values of the initial rotational state. In the figure shown below, the L = L' + 1 absorption spectrum of NO at 120 °K is given. The intensities of the various peaks are related to the populations of the lower-energy rotational states which are, in turn, proportional to \((2 L' + 1) e^{(- L'(L'+1) \dfrac{\hbar^2}{8\pi^2IkT}}.\) Also included in the intensities are so-called line strength factors that are proportional to the squares of the quantities:
\[ \mu \sqrt{ (2L + 1)(2L' + 1)\dfrac{3}{4\pi} }\left( \dfrac{\text{L' 1 L}}{M' m -M} \right) \left( \dfrac{\text{L' 1 L}}{\text{0 0 -0}} \right)(-1)^M \nonumber \]
which appear in the E1 integrals analyzed above (recall that the rate of photon absorption \( R_{i,f} = \left( \frac{2\pi}{\hbar^2} \right)g(\omega_{f,i}) | \textbf{E}_0\cdot{\langle}\Phi_f | \mu | \Phi_i \rangle |^2 \) involves the squares of these matrix elements). The book by Zare gives an excellent treatment of line strength factors' contributions to rotation, vibration, and electronic line intensities.
Non-Linear Molecules
For molecules that are non-linear and whose rotational wavefunctions are given in terms of the spherical or symmetric top functions \(\textbf{D}^{\text{*}}_{\text{L,M,K}}\), the dipole moment \(\mu_{ave}\) can have components along any or all three of the molecule's internal coordinates (e.g., the three molecule-fixed coordinates that describe the orientation of the principal axes of the moment of inertia tensor). For a spherical top molecule, \(| \mu_{ave} |\) vanishes, so E1 transitions do not occur.
For symmetric top species, \(\mu_{ave}\) lies along the symmetry axis of the molecule, so the orientation of \(\mu_{ave}\) can again be described in terms of \(\theta \text{ and } \phi \), the angles used to locate the orientation of the molecule's symmetry axis relative to the lab-fixed coordinate system. As a result, the E1 integral again can be decomposed into three pieces:
\[ \langle \phi_{ir} | \mu_{ave} | \phi_{fr}\rangle_x = \mu\int D_{\text{L, M, K}}(\theta ,\phi ,\chi)\text{ cos}\theta \text{ cos}\phi D^{\text{*}}_{\text{L', M', K'}}(\theta , \phi , \chi)\text{ sin}\theta \text{ d}\theta \text{ d}\phi \text{ d}\chi \nonumber \]
\[ \langle \phi_{ir} | \mu_{ave} | \phi_{fr}\rangle_y = \mu\int D_{\text{L, M, K}}(\theta ,\phi ,\chi)\text{ cos}\theta \text{ sin}\phi D^{\text{*}}_{\text{L', M', K'}}(\theta , \phi , \chi)\text{ sin}\theta \text{ d}\theta \text{ d}\phi \text{ d}\chi \nonumber \]
\[ \langle \phi_{ir} | \mu_{ave} | \phi_{fr}\rangle_z = \mu\int D_{\text{L, M, K}}(\theta ,\phi ,\chi) \text{ cos}\theta D^{\text{*}}_{\text{L', M', K'}}(\theta , \phi , \chi)\text{ sin}\theta \text{ d}\theta \text{ d}\phi \text{ d}\chi \nonumber \]
Using the fact that \( \text{ cos}\theta \propto \text{D}^{\text{*}}_{\text{1, 0,0}}; \text{ sin}\theta \text{ cos}\phi \propto \text{D}^{\text{*}}_{\text{1,1,0}} + \text{D}^{\text{*}}_{\text{1,-1,0}}; \text{ and sin}\theta \text{ sin}\phi \propto \text{D}^{\text{*}}_{\text{1,1,0}} - \text{D}^{\text{*}}_{\text{1,-1,0}}\) and the tools of angular momentum coupling allows these integrals to be expressed, as above, in terms of products of the following 3-j symbols:
\[ \left( \dfrac{\text{L' 1 L}}{\text{M' m -M}} \right) \left( \dfrac{\text{L' 1 L}}{\text{K' 0 -K}} \right), \nonumber \]
from which the following selection rules are derived:
\[ \text{L} = \text{L' + 1, L', L' - 1} \text{ (but not L = L' = 0)} \nonumber \]
\[ \text{K = K'} \nonumber \]
\[ \text{M = M' + m,} \nonumber \]
with m = 0 for the Z-axis integral and m = ± 1 for the X- and Y- axis integrals. In addition, if K = K' = 0, the L = L' transitions are also forbidden by the second 3-j symbol vanishing.


