13.1: Rotational Motions of Rigid Molecules
- Page ID
- 64790
In Chapter 3 and Appendix G the energy levels and wavefunctions that describe the rotation of rigid molecules are described. Therefore, in this Chapter these results will be summarized briefly and emphasis will be placed on detailing how the corresponding rotational Schrödinger equations are obtained and the assumptions and limitations underlying them.
Linear Molecules
As given in Chapter 3, the Schrödinger equation for the angular motion of a rigid (i.e., having fixed bond length R) diatomic molecule is
\[ \dfrac{\hbar^2}{2\mu}\left[ \dfrac{1}{R^2 \sin \theta}\dfrac{\partial}{\partial \theta} \left( \sin \theta \dfrac{\partial}{\partial \theta} \right) + \left( \dfrac{1}{R^2\sin^2\theta} \right) \dfrac{\partial^2}{\partial \phi^2} \right] \psi = E \psi \nonumber \]
or more succinctly in terms of the angular momentum operator as
\[ \dfrac{L^2\psi}{2\mu R^2} = E \psi \nonumber \]
The Hamiltonian in this problem contains only the kinetic energy of rotation; no potential energy is present because the molecule is undergoing unhindered "free rotation". The angles \( \theta \text{ and } \phi\) describe the orientation of the diatomic molecule's axis relative to a laboratory-fixed coordinate system, and \(\mu\) is the reduced mass of the diatomic molecule
\[\mu=\dfrac{m_1m_2}{m_1+m_2}. \nonumber \]
The Eigenfunctions and Eigenvalues
The eigenvalues corresponding to each eigenfunction are straightforward to find because \(H_{rot}\) is proportional to the \(L^2\) operator whose eigenvalues have already been determined. The resultant rotational energies are given as:
\[ E_J = \hbar ^2\dfrac{J(J+1)}{(2\mu R^2)} = BJ(J+1) \nonumber \]
and are independent of \(M\). Thus each energy level is labeled by \(J\) and is \(2J+1\)-fold degenerate (because \(M\) ranges from \(-J\) to \(J\)). The rotational constant B (defined as \(\hbar^2/2\mu R^2\) depends on the molecule's bond length and reduced mass. Spacings between successive rotational levels (which are of spectroscopic relevance because angular momentum selection rules often restrict \(\Delta J\) to 1,0, and -1) are given by
\[ \Delta E = B(J+1)(J+2) - BJ(J+1) = 2B(J+1). \nonumber \]
Within this "rigid rotor" model, the absorption spectrum of a rigid diatomic molecule should display a series of peaks, each of which corresponds to a specific \(J \rightarrow J + 1\) transition. The energies at which these peaks occur should grow linearly with J. An example of such a progression of rotational lines is shown in the figure below.
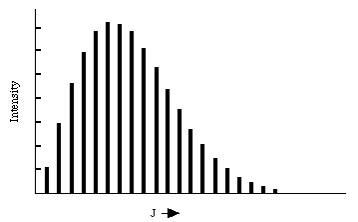
The energies at which the rotational transitions occur appear to fit the \(\Delta E = 2B (J+1)\) formula rather well. The intensities of transitions from level J to level J+1 vary strongly with J primarily because the population of molecules in the absorbing level varies with J. These populations PJ are given, when the system is at equilibrium at temperature T, in terms of the degeneracy (2J+1) of the \(J^{th}\) level and the energy of this level B J(J+1) :
\[ P_J = Q^{-1}(2J+1) e^{\dfrac{-BJ(J+1)}{kT}}, \nonumber \]
where \(Q\) is the rotational partition function:
\[ Q = \sum\limits_J (2J+1)e^{\dfrac{-BJ(J+1)}{kT}}. \nonumber \]
For low values of \(J\), the degeneracy is low and the \(e^{\frac{-BJ(J+1)}{kT}}\) factor is near unity. As J increases, the degeneracy grows linearly but the \(e^{\frac{-BJ(J+1)}{kT}}\) factor decreases more rapidly. As a result, there is a value of J, given by taking the derivative of \((2J+1)e^{- \frac{BJ(J+1)}{kT}}\) with respect to J and setting it equal to zero,
\[ 2J_max + 1 = \sqrt{\dfrac{2kT}{B}} \nonumber \]
at which the intensity of the rotational transition is expected to reach its maximum.
The eigenfunctions belonging to these energy levels are the spherical harmonics \(Y_{L,M}(\theta ,\phi)\) which are normalized according to
\[ \int\limits^\pi_0 \int\limits^{2\pi}_0 Y^{\text{*}}_{L,M}(\theta ,\phi) Y_{L',M'}(\theta ,\phi) sin\theta d\theta d\phi = \delta_{L,L'}\delta_{M,M'}. \nonumber \]
These functions are identical to those that appear in the solution of the angular part of Hydrogen-like atoms. The above energy levels and eigenfunctions also apply to the rotation of rigid linear polyatomic molecules; the only difference is that the moment of inertia \(I\) entering into the rotational energy expression is given by
\[ I = \sum \limits_am_a R_a^2 \nonumber \]
where \(m_a\) is the mass of the \(a^{th} \text{ atom and } R_a\) is its distance from the center of mass of the molecule. This moment of inertia replaces \(mR^2\) in the earlier rotational energy level expressions.
Non-Linear Molecules
The rotational kinetic energy operator for a rigid polyatomic molecule is shown in Appendix G to be
\[ H_{rot} = \dfrac{J_b^2}{2I_a} + \dfrac{J_b^2}{2I_b} + \dfrac{J_c^2}{2I_c} \nonumber \]
where the \(I_k\) (k = a, b, c) are the three principal moments of inertia of the molecule (the eigenvalues of the moment of inertia tensor). This tensor has elements in a Cartesian coordinate system (K, K' = X, Y, Z) whose origin is located at the center of mass of the molecule that are computed as:
\[ I_{K,K} \sum\limits_j m_j (R_j^2 - R^2_{K,j}) (\text{for K = K'}) \nonumber \]
\[ I_{K,K'} = -\sum\limits_jm_jR_{K,j}R_{K',j} (\text{ for K }\neq\text{ K'}). \nonumber \]
The components of the quantum mechanical angular momentum operators along the three principal axes are:
\[ J_a = -i\hbar \cos \chi \left[ \cot \theta \dfrac{\partial}{\partial \chi} - \dfrac{1}{\sin \theta} \dfrac{\partial}{\partial \phi} \right] - -i\hbar \sin\chi \dfrac{\partial}{\partial \theta} \nonumber \]
\[ J_b = i\hbar \sin \chi \left[ \cot \theta \dfrac{\partial}{\partial \chi}- \dfrac{1}{\sin\theta}\dfrac{\partial}{\partial \phi} \right]- -i\hbar \cos\chi \dfrac{\partial}{\partial \theta} \nonumber \]
\[ J_c = -i\hbar\dfrac{\partial}{\partial \chi}. \nonumber \]
The angles \(\theta, \phi, \text{ and } \chi\) are the Euler angles needed to specify the orientation of the rigid molecule relative to a laboratory-fixed coordinate system. The corresponding square of the total angular momentum operator \(J^2\) can be obtained as
\[ J^2 = J_a^2 + J_b^2 + J_c^2 = -\dfrac{\partial^2}{\partial\theta^2} - cot\theta \dfrac{\partial}{\partial \theta} - \dfrac{1}{sin\theta}\left( \dfrac{\partial^2}{\partial\phi^2} + \dfrac{\partial^2}{\partial\chi^2} - 2cos\theta \dfrac{\partial^2}{\partial\phi\partial\chi}\right), \nonumber \]
and the component along the lab-fixed Z axis \(J_Z \text{ is } -i\hbar\frac{\partial}{\partial \phi}.\)
The Eigenfunctions and Eigenvalues for Special Cases
Spherical Tops
When the three principal moment of inertia values are identical, the molecule is termed a spherical top. In this case, the total rotational energy can be expressed in terms of the total angular momentum operator \(J^2\)
\[ H_{rot} = \dfrac{J^2}{2I} \nonumber \]
As a result, the eigenfunctions of \(H_{rot}\) are those of \(J^2\) (and \(J_a \text{ as well as }J_Z \text{ both of which commute with }J^2 \text{ and with one another; } J_Z \) is the component of J along the lab-fixed Z-axis and commutes with \(J_a \text{ because } J_Z = - i\hbar\frac{\partial}{\partial \phi} \text{ and } J_a = -i\hbar\frac{\partial}{\partial\chi}\) act on different angles). The energies associated with such eigenfunctions are
\[ E(J,M,K) = \hbar^2\dfrac{J(J+1)}{2I^2}, \nonumber \]
for all K (i.e., \(J_a\) quantum numbers) ranging from -J to J in unit steps and for all M (i.e., \(J_Z\) quantum numbers) ranging from -J to J. Each energy level is therefore \((2J + 1)^2\) degenarate because there are 2J + 1 possible K values and 2J + 1 possible M values for each J.
The eigenfunctions of \(J^2, J_Z \text{ and } J_a , |J,M,K \rangle\) are given in terms of the set of rotation matrices \(D_{J,M,K}:\)
\[ |J,M,K \rangle = \sqrt{\dfrac{2J + 1}{8\pi^2}}D^{\text{*}}_{J,M,K}(\theta ,\phi ,\chi) \nonumber \]
which obey
\[ J^2|J,M,K \rangle = \hbar^2 J(J+1) |J,M,K\rangle, \nonumber \]
\[ J_a|J,M,K\rangle = \hbar K|J,M,K\rangle, \nonumber \]
\[ J_Z|J,M,K\rangle = \hbar M|J,M,K\rangle. \nonumber \]
Symmetric Tops
Molecules for which two of the three principal moments of inertia are equal are called symmetric tops. Those for which the unique moment of inertia is smaller than the other two are termed prolate symmetric tops; if the unique moment of inertia is larger than the others, the molecule is an oblate symmetric top. Again, the rotational kinetic energy, which is the full rotational Hamiltonian, can be written in terms of the total rotational angular momentum operator \(J^2\) and the component of angular momentum along the axis with the unique principal moment of inertia:
\[ H_{rot} = \dfrac{J^2}{2I} + J_a^2\left[ \dfrac{1}{2I_a} - \dfrac{1}{2I} \right] \nonumber \]
for prolate tops and
\[ H_{rot} = \dfrac{J^2}{2I} + J_c^2\left[ \dfrac{1}{2I_c} - \dfrac{1}{2I}\right] \nonumber \]
for oblate tops.
As a result, the eigenfunctions of \(H_{rot} \text{are those of }J^2 \text{ and } J_a \text{ or }J_c \text{ (and of }J_Z)\), and the corresponding energy levels are:
\[ E(J,K,M) = \hbar^2\dfrac{J(J+1)}{2I^2} + \hbar^2K^2\left[ \dfrac{1}{2I_a} - \dfrac{1}{2I} \right], \nonumber \]
for prolate toops
\[ E(J,K,M) = \hbar \dfrac{J(J+1)}{2I^2} + \hbar^2K^2 \left[ \dfrac{1}{2I_a} - \dfrac{1}{2I} \right], \nonumber \]
for oblate tops, again for K and M (i.e., \(J_a \text{ or } J_c \text{ and } J_Z\) quantum numbers, respectively) ranging from -J to J in unit steps. Since the energy now depends on K, these levels are only 2J + 1 degenerate due to the 2J + 1 different M values that arise for each J value. The eigenfunctions \(|J, M,K \rangle\) are the same rotation matrix functions as arise for the spherical-top case.
Asymmetric Tops
The rotational eigenfunctions and energy levels of a molecule for which all three principal moments of inertia are distinct (a so-called asymmetric top) can not easily be expressed in terms of the angular momentum eigenstates and the J, M, and K quantum numbers. However, given the three principal moments of inertia \(I_a, I_b, \text{ and } I_c\), a matrix representation of each of the three contributions to the rotational Hamiltonian
\[ H_{rot} = \dfrac{J_a^2}{2I_a} + \dfrac{J_b^2}{2I_b} + \dfrac{J_c^2}{2I_c} \nonumber \]
can be formed within a basis set of the {|J, M, K>} rotation matrix functions. This matrix will not be diagonal because the |J, M, K> functions are not eigenfunctions of the asymmetric top \(H_{rot}\). However, the matrix can be formed in this basis and subsequently brought to diagonal form by finding its eigenvectors {\(C_{n,J,M,K}\) and its eigenvalues \(\{E_n\}\). The vector coefficients express the asymmetric top eigenstates as
\[ \Psi_n(\theta , \phi , \chi ) = \sum\limits_{J, M, K} C_{n, J, M, K}|J, M, K\rangle. \nonumber \]
Because the total angular momentum \(J^2\) still commutes with \(H_{rot}\), each such eigenstate will contain only one J-value, and hence \(\Psi_n\) can also be labeled by a J quantum number:
\[ \Psi_{n,J}(\theta , \phi, \chi) = \sum\limits_{M,K} C_{n, J, M, K} |J, M, K\rangle. \nonumber \]
To form the only non-zero matrix elements of \(H_{rot}\) within the \(|J, M, K \rangle\) basis, one can use the following properties of the rotation-matrix functions:
\[ \langle J, M, K| J_a^2 | J, M, K \rangle =\langle J, M, K| J_b^2 |J, M, K \rangle = \dfrac{1}{2} \langle J,M, K| J^2 - J_c^2 | J, M, K \rangle = \hbar^2 [J(J+1) - K^2], \nonumber \]
\[ \langle J, M, K | J_c^2 |J, M, K \rangle = \hbar^2 K^2, \nonumber \]
\[ \langle J, M, K| J_a^2 | J, M, K \pm 2 \rangle = -\langle J, M, K | J_b^2 | J, M, K \pm 2 \rangle = \hbar^2 \sqrt{J(J+1) - K(K\pm 1}\sqrt{J(J+1) - (K \pm 1)(K \pm 2)} \nonumber \]
\[ \langle J, M, K| J_c^2 | J, M, K \pm 2 \rangle = 0. \nonumber \]
Each of the elements of \(J_c^2, J_a^2, \text{ and }J_b^2\) must, of course, be multiplied, respectively, by \( \frac{1}{2I_c}, \frac{1}{2I_a} \text{ and } \frac{1}{2I_b}\) summed together to form the matrix representation of \(H_{rot}.\) The diagonalization of this matrix then provides the asymmetric top energies and wavefunctions.


