10.4: Atomic Term Symbols and Wavefunctions
- Page ID
- 60599
Non-Equivalent Orbital Term Symbols
When coupling non-equivalent angular momenta (e.g., a spin and an orbital angular momenta or two orbital angular momenta of non-equivalent electrons), one vector couples using the fact that the coupled angular momenta range from the sum of the two individual angular momenta to the absolute value of their difference. For example, when coupling the spins of two electrons, the total spin S can be 1 or 0; when coupling a p and a d orbital, the total orbital angular momentum can be 3, 2, or 1. Thus for a \(p^1d^1\) electronic configuration, \(^3F, ^1F, ^3D, ^1D, ^3P, \text{ and } ^1P\) energy levels (and corresponding wavefunctions) arise. The energy differences among these levels has to do with the different electron-electron repulsions that occur in these levels; that is, their wavefunctions involve different occupancy of the p and d orbitals and hence different repulsion energies. If spin-orbit coupling is present, the L and S angular momenta are further vector coupled. For example, the \(^3F\) level splits into J= 4, 3, and 2 levels which are denoted \(^3F_4, ^3F_3, \text{ and } ^3F_2.\) The energy differences among these J-levels are caused by spin-orbit interactions.

Equivalent Orbital Term Symbols
If equivalent angular momenta are coupled (e.g., to couple the orbital angular momenta of a \(p^2 \text{ or } d^3\) configuration), one must use the "box" method to determine which of the term symbols, that would be expected to arise if the angular momenta were nonequivalent, violate the Pauli principle. To carry out this step, one forms all possible unique (determinental) product states with non-negative \( M_L \text{ and } M_S\) values and arranges them into groups according to their \(M_L \text{ and } M_S\) values. For example, the boxes appropriate to the \(p^2\) orbital occupancy are shown below:

There is no need to form the corresponding states with negative \(M_L \text{ or negative } M_S\) values because they are simply "mirror images" of those listed above. For example, the state with \(M_L= -1 \text{ and } M_S = -1 \text{ is } |p_{-1}\beta p_0\beta|,\) which can be obtained from the \(M_L = 1, M_S = 1\) state \(|p1\alpha p_0\alpha|\) by replacing \(\alpha \text{ by } \beta\) and replacing \(p_1 \text{ by } p_{-1}\).
Given the box entries, one can identify those term symbols that arise by applying the following procedure over and over until all entries have been accounted for:
- One identifies the highest \(M_S\) value (this gives a value of the total spin quantum number that arises, S) in the box. For the above example, the answer is S = 1.
- For all product states of this \(M_S\) value, one identifies the highest \(M_L\) value (this gives a value of the total orbital angular momentum, L, that can arise for this S ). For the above example, the highest \(M_L \text{ within the } M_S =1 \text{ states is } M_L = 1 \text{ (not } M_L = 2),\text{ hence }L=1.\)
- Knowing an S, L combination, one knows the first term symbol that arises from this configuration. In the \(p^2\) example, this is \(^3P.\)
- Because the level with this L and S quantum numbers contains (2L+1)(2S+1) states with \(M_L \text{ and } M_S\) quantum numbers running from -L to L and from -S to S, respectively, one must remove from the original box this number of product states. To do so, one simply erases from the box one entry with each such ML and MS value. Actually, since the box need only show those entries with non-negative ML and MS values, only these entries need be explicitly deleted. In the \(^3P\) example, this amounts to deleting nine product states with \(M_L, M_S\) values of 1,1; 1,0; 1,-1; 0,1; 0,0; 0,-1; -1,1; -1,0; -1,-1.
- After deleting these entries, one returns to step 1 and carries out the process again. For the \(p^2\) example, the box after deleting the first nine product states looks as follows (those that appear in italics should be viewed as already cancelled in counting all of the \(^3P\) states):

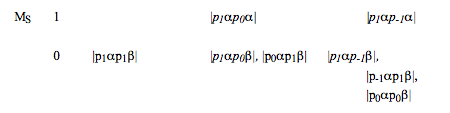
It should be emphasized that the process of deleting or crossing off entries in various \(M_L, M_S\) boxes involves only counting how many states there are; by no means do we identify the particular \(L,S,M_L,M_S\) wavefunctions when we cross out any particular entry in a box. For example, when the \(\lvert p_1\alpha p_0\beta \rvert\) product is deleted from the \(M_L= 1, M_S=0\) box in accounting for the states in the \(^3P\) level, we do not claim that \(|p_1\alpha p_0\beta|\) itself is a member of the \(^3P\) level; the \(|p_0\alpha p_1\beta|\) product state could just as well been eliminated when accounting for the \(^3P\) states. As will be shown later, the \(^3P\) state with \(M_L= 1, M_S=0\) will be a combination of \(|p_1\alpha p_0\beta| \text{ and } |p_0\alpha p_1\beta|.\)
Returning to the \(p^2\) example at hand, after the \(^3P\) term symbol's states have been accounted for, the highest \(M_S\) value is 0 (hence there is an S=0 state), and within this \(M_S\) value, the highest \(M_L\) value is 2 (hence there is an L=2 state). This means there is a \(^1D\) level with five states having \(M_L\) = 2,1,0,-1,-2. Deleting five appropriate entries from the above box (again denoting deletions by italics) leaves the following box:
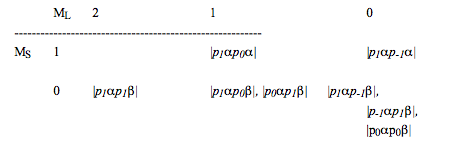
The only remaining entry, which thus has the highest \(M_S \text{ and } M_L\) values, has \(M_S = 0 \text{ and } M_L = 0.\) Thus there is also a \(^1S\) level in the \(p^2\) configuration.
Thus, unlike the non-equivalent \(^2p1^3p1\) case, in which \(^3P, ^1P, ^3D, ^1D, ^3S, \text{ and } ^1S\) levels arise, only the \(^3P, ^1D, \text{ and } ^1S\) arise in the \(p^2\) situation. This "box method" is necessary to carry out whenever one is dealing with equivalent angular momenta.
If one has mixed equivalent and non-equivalent angular momenta, one can determine all possible couplings of the equivalent angular momenta using this method and then use the simpler vector coupling method to add the non-equivalent angular momenta to each of these coupled angular momenta. For example, the \(p^2d^1\) configuration can be handled by vector coupling (using the straightforward non-equivalent procedure) L=2 (the d orbital) and \( S= \frac{1}{2}\) (the third electron's spin) to each of \(^3P, ^1D, \text{ and } ^1S.\) The result is \(^4F, ^4D, ^4P, ^2F, ^2D, ^2P, ^2G, ^2F, ^2D, ^2P, ^2S, \text{ and } ^2D.\)


