8.4: Configuration Interaction (CI) Describes the Correct Electronic States
- Page ID
- 62624
The most commonly employed tool for introducing such spatial correlations into electronic wavefunctions is called configuration interaction (CI); this approach is described briefly later in this Section and in considerable detail in Section 6. Briefly, one employs the (in principle, complete as shown by P. O. Löwdin, Rev. Mod. Phys. 32 , 328 (1960)) set of N-electron configurations that
- can be formed by placing the N electrons into orbitals of the atom or molecule under study, and that
- possess the spatial, spin, and angular momentum symmetry of the electronic state of interest.
This set of functions is then used, in a linear variational function, to achieve, via the CI technique, a more accurate and dynamically correct description of the electronic structure of that state. For example, to describe the ground 1S state of the Be atom, the 1s22s2 configuration (which yields the mean-field description) is augmented by including other configurations such as \( 1s^23s^2 \text{ , } 1s^22p^2 \text{ , } 1s^23p^2 \text{ , } 1s^22s^3s \text{ , } 3s^22s^2 \text{ , } 2p^22s^2, \)etc., all of which have overall \(^1S\) spin and angular momentum symmetry. The excited \(^1S\) states are also combinations of all such configurations. Of course, the ground-state wavefunction is dominated by the \( |1s^22s^2|\) and excited states contain dominant contributions from \(|1s^22s3s|\), etc. configurations. The resultant CI wavefunctions are formed as shown in Section 6 as linear combinations of all such configurations.
To clarify the physical significance of mixing such configurations, it is useful to consider what are found to be the two most important such configurations for the ground 1S state of the Be atom:
\[ \Psi \cong C_1 |1_s^22s^2| - C_2 \left[ |1s^22p_x^2| + |1s^22p_y^2| + |1s^22p_z^2| \right] . \nonumber \]
As proven in Chapter 13.III, this two-configuration description of Be's electronic structure is equivalent to a description is which two electrons reside in the 1s orbital (with opposite, \(\alpha \text{ and } \beta\) spins) while the other pair reside in 2s-2p hybrid orbitals (more correctly, polarized orbitals) in a manner that instantaneously correlates their motions:
\begin{align} \Psi \cong \dfrac{1}{6} C_1 |1s^2& \{ \left[ (2s-a2p_x)\alpha (2s + a2p_x)\beta - (2s - a2p_x)\beta (2s + a2p_x)\alpha \right] \\ &+ \left[ (2s - a2p_y)\alpha (2s + a2p_y) \beta - (2s - a2p_y) \beta (2s + a2p_y)\alpha \right] \\ &+ \left[ (2s - a2p_z)\alpha (2s + a2p_z)\beta - (2s - a2p_z )\beta (2s + a2p_z )\alpha \right] \}|, \end{align}
where \( a = \sqrt{3\dfrac{C_2}{C_1}}.\)
The so-called polarized orbital pairs \((2s \pm a 2p_{x,y, \text{ or } z}\)) are formed by mixing into the 2s orbital an amount of the \(2_{px,y, \text{ or } z}\) orbital, with the mixing amplitude determined by the ratio of \(C_2 \text{ to } C_1\). As will be detailed in Section 6, this ratio is proportional to the magnitude of the coupling \( \langle |1s^22s^2 |H| 1s^22p^2|\rangle \) between the two configurations and inversely proportional to the energy difference \( \left[ \langle |1s^22s^2 |H| 1s^22s^2| \rangle - \langle |1s^22p^2 |H| 1s^22p^2 |\rangle \right] \) for these configurations. So, in general, configurations that have similar energies (Hamiltonian expectation values) and couple strongly give rise to strongly mixed polarized orbital pairs. The result of forming such polarized orbital pairs are described pictorially below.
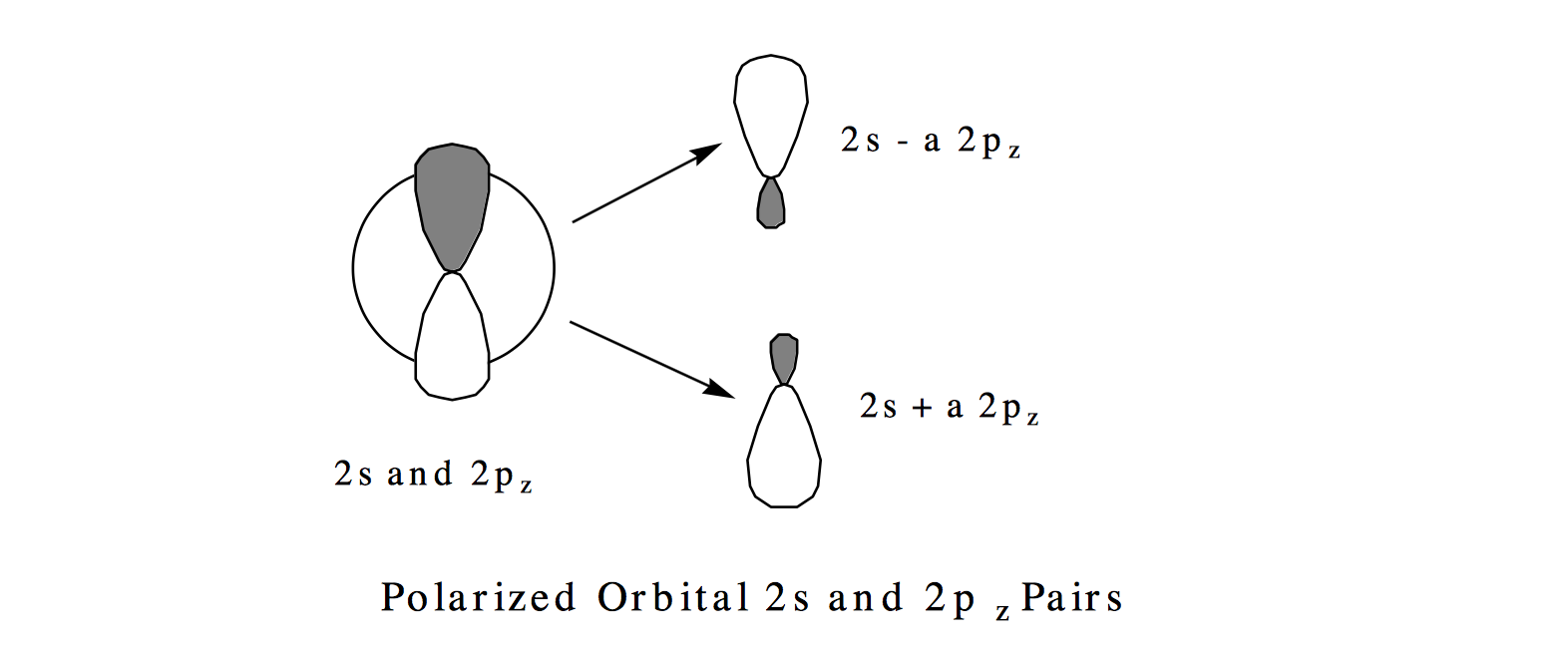
In each of the three equivalent terms in this wavefunction, one of the valence electrons moves in a 2s+a2p orbital polarized in one direction while the other valence electron moves in the 2s-a2p orbital polarized in the opposite direction. For example, the first term \( \left[ (2s - a2p_x)\alpha (2s + a2p_x)\beta - (2s-a2p_x)\beta (2s + a2p_x)\alpha \right] \) describes one electron occupying a \(2s-a2p_x\) polarized orbital while the other electron occupies the \( 2s+a2p_x\) orbital. In this picture, the electrons reduce their mutual coulomb repulsion by occupying different regions of space; in the SCF mean-field picture, both electrons reside in the same 2s region of space. In this particular example, the electrons undergo angular correlation to "avoid" one another. The fact that equal amounts of x, y, and z orbital polarization appear in Y is what preserves the \(^1S\) symmetry of the wavefunction.
The fact that the CI wavefunction
\[ \Psi \cong C_1 |1s^22s^ - C_2 \left[ |1s^22p_x^2| + |1s^22p_y^2| + |1s^22p_z^2 | \right] \nonumber \]
mixes its two configurations with opposite sign is of significance. As will be seen later in Section 6, solution of the Schrödinger equation using the CI method in which two configurations (e.g., \( |1s^22s^2| \text{ and } |1s^22p^2|)\) are employed gives rise to two solutions. One approximates the ground state wave function; the other approximates an excited state. The former is the one that mixes the two configurations with opposite sign.
To understand why the latter is of higher energy, it suffices to analyze a function of the form
\[ \Psi ' \cong C_1 |1s^22s^2| + C_2 \left[ |1s^22p_x^2| + |1s^22p_y^2| + |1s^22p_z^2| \right] \nonumber \]
in a manner analogous to above. In this case, it can be shown that
\begin{align} \Psi ' \cong \dfrac{1}{6} C_1 |1s^2&\{ \left[ (2s - ia2p_x)\alpha (2s + ia2p_x)\beta - (2s - ia2p_x)\beta (2s + ia2p_x)\alpha \right] \\ &+\left[ (2s - ia2p_y)\alpha (2s + ia2p_y)\beta - (2s - ia2p_y)\beta (2s + ia2p_y)\alpha \right] \\ &+\left[ (2s - ia2p_z)\alpha (2s + ia2p_z)\beta - (2s - ia2p_z)\beta (2s + ia2p_z)\alpha \right] | \}.\end{align}
There is a fundamental difference, however, between the polarized orbital pairs introduced earlier \( \phi_{\pm} = (2s \pm a2p_{x,y, \text{ or } z}) \) and the corresponding functions \( \phi_{\pm}' = ( 2s \pm ia2p_{x, y \text{ or }z} ) \) appearing here. The probability densities embodied in the former
\[ |\phi_{\pm}|^2 = |2s|^2 + a^2 ||^2 \pm 2a(2s 2p_{x,y \text{ or } z}) \nonumber \]
describe constructive (for the + case) and destructive (for the - case) superposition of the probabilities of the 2s and 2p orbitals. The probability densities of \( \phi_{\pm}'\) are
\begin{align} |\phi_{\pm}'|^2 &= \left( 2s \pm ia2p_{x,y \text{ or }z} \right) *\left( 2s \pm ia2p_{x,y \text{ or } z} \right) \\ &= |2s|^2 + a^2|2p_{x,y \text{ or } z}|^2 .\end{align}
These densities are identical to one another and do not describe polarized orbital densities. Therefore, the CI wavefunction which mixes the two configurations with like sign, when analyzed in terms of orbital pairs, places the electrons into orbitals \( \phi_{\pm}' = \left( 2s \pm ia2p_{x,y, \text{ or }z} \right) \) whose densities do not permit the electrons to avoid one another. Rather, both orbitals have the same spatial density \( |2s|^2 + a^2 |2p_{x,y, \text{ or } z}|^2\), which gives rise to higher coulombic interaction energy for this state.


