1.5: Particles in Boxes
- Page ID
- 60540
The particle-in-a-box problem provides an important model for several relevant chemical situations
The above 'particle in a box' model for motion in two dimensions can obviously be extended to three dimensions or to one. For two and three dimensions, it provides a crude but useful picture for electronic states on surfaces or in crystals, respectively. Free motion within a spherical volume gives rise to eigenfunctions that are used in nuclear physics to describe the motions of neutrons and protons in nuclei. In the so-called shell model of nuclei, the neutrons and protons fill separate s, p, d, etc orbitals with each type of nucleon forced to obey the Pauli principle. These orbitals are not the same in their radial 'shapes' as the s, p, d, etc orbitals of atoms because, in atoms, there is an additional radial potential
\[V(r) = -Z \dfrac{e^2}{r} \nonumber \]
present. However, their angular shapes are the same as in atomic structure because, in both cases, the potential is independent of \(\theta\) and \(\phi\). This same spherical box model has been used to describe the orbitals of valence electrons in clusters of mono-valent metal atoms such as Cs\(_n\), Cu\(_n\), Na\(_n\) and their positive and negative ions. Because of the metallic nature of these species, their valence electrons are sufficiently delocalized to render this simple model rather effective (see T. P. Martin, T. Bergmann, H. Göhlich, and T. Lange, J. Phys. Chem. 95 , 6421 (1991)).
One-dimensional free particle motion provides a qualitatively correct picture for \(\pi\)-electron motion along the p\(_\pi\) orbitals of a delocalized polyene. The one cartesian dimension then corresponds to motion along the delocalized chain. In such a model, the box length L is related to the carbon-carbon bond length R and the number N of carbon centers involved in the delocalized network L=(N-1)R. Below, such a conjugated network involving nine centers is depicted. In this example, the box length would be eight times the C-C bond length.
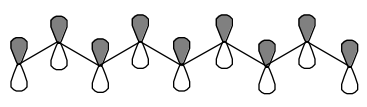
Conjugated \(\pi\) Network with 9 Centers Involved
The eigenstates \(\psi_n\)(x) and their energies E\(_n\) represent orbitals into which electrons are placed. In the example case, if nine \(\pi\) electrons are present (e.g., as in the 1,3,5,7- nonatetraene radical), the ground electronic state would be represented by a total wavefunction consisting of a product in which the lowest four \(\psi\)'s are doubly occupied and the fifth \(\psi\) is singly occupied:
\[ \Psi = \psi_1\alpha\psi_1\beta\psi_2\alpha\psi_2\beta\psi_3\alpha\psi_3\beta\psi_4\alpha\psi_4\beta\psi_5\alpha. \nonumber \]
A product wavefunction is appropriate because the total Hamiltonian involves the kinetic plus potential energies of nine electrons. To the extent that this total energy can be represented as the sum of nine separate energies, one for each electron, the Hamiltonian allows a separation of variables
\[H \cong \sum\limits_j H(j) \nonumber \]
in which each H(j) describes the kinetic and potential energy of an individual electron. This (approximate) additivity of H implies that solutions of H \(\Psi\) = E \(\Psi\) are products of solutions to
\[H (j) \psi(\textbf{r}_j) = E_j \psi(\textbf{r}_j). \nonumber \]
The two lowest \(\pi\)-excited states would correspond to states of the form
\[ \Psi^* = \psi_1\alpha \psi_1 \beta \psi_2 \alpha \psi_2 \beta \psi_3\alpha \psi_3\beta \psi_4 \alpha \psi_5 \beta \psi_5 \alpha \nonumber \]
and
\[ \Psi'^* = \psi_1 \alpha \psi_1 \beta \psi_2 \alpha \psi_2\beta \psi_3 \alpha \psi_3 \beta \psi_4 \alpha \psi_4 \beta \psi_6 \alpha, \nonumber \]
where the spin-orbitals (orbitals multiplied by \(\alpha\) or \(\beta\)) appearing in the above products depend on the coordinates of the various electrons. For example,
\[\psi_1\alpha \psi_1 \beta \psi_2 \alpha \psi_2 \beta \psi_3\alpha \psi_3\beta \psi_4 \alpha \psi_5 \beta \psi_5 \alpha \nonumber \]
denotes
\[\psi_1\alpha(\textbf{r}_1) \psi_1 \beta(\textbf{r}_2) \psi_2 \alpha(\textbf{r}_3) \psi_2 \beta (\textbf{r}_4) \psi_3\alpha (\textbf{r}_5) \psi_3\beta (\textbf{r}_6)\psi_4 \alpha (\textbf{r}_7) \psi_5 \beta (\textbf{r}_8) \psi_5 \alpha (\textbf{r}_9) \nonumber \]
The electronic excitation energies within this model would be
\[ \Delta E^{\text{*}} = \pi^2 \dfrac{\hbar^2}{2m}\left[ \dfrac{5^2}{L^2} - \dfrac{4^2}{L^2} \right] \nonumber \]
and
\[ \Delta E'* = \pi^2 \dfrac{\hbar^2}{2m} \left[ \dfrac{6^2}{L^2} - \dfrac{5^2}{L^2} \right] , \nonumber \]
for the two excited-state functions described above. It turns out that this simple model of \(\pi\)-electron energies provides a qualitatively correct picture of such excitation energies.
This simple particle-in-a-box model does not yield orbital energies that relate to ionization energies unless the potential 'inside the box' is specified. Choosing the value of this potential V\(_0\) such that
\[V_0 + \pi^2 \dfrac{\hbar^2}{2m} \left[ \dfrac{5^2}{L^2}\right] \nonumber \]
is equal to minus the lowest ionization energy of the 1,3,5,7-nonatetraene radical, gives energy levels \(\left( \text{as } E = V_0 + \pi^2 \dfrac{\hbar^2}{2m} \left[ \dfrac{n^2}{L^2} \right] \right)\) which then are approximations to ionization energies.
The individual p-molecular orbitals
\[ \psi_n = \sqrt{ \dfrac{2}{L} } \sin \left(\dfrac{n\pi x}{L}\right) \nonumber \]
are depicted in the figure below for a model of the 1,3,5 hexatriene \(\pi\)-orbital system for which the 'box length' L is five times the distance \(R_{CC}\) between neighboring pairs of Carbon atoms.
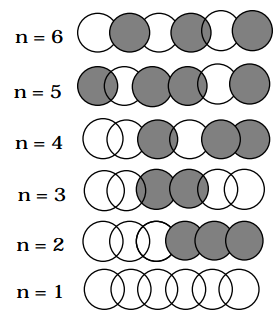
\[ \sqrt{\dfrac{2}{L}} \sin \left( \dfrac{n \pi x}{L} \right); L =5 xR_{CC} \nonumber \]
In this figure, positive amplitude is denoted by the clear spheres and negative amplitude is shown by the darkened spheres; the magnitude of the k\(^{th}\) C-atom centered atomic orbital in the n\(^{th}\) \(pi\)-molecular orbital is given by
\[ \sqrt{\dfrac{2}{L}}\sin \left(\dfrac{n\pi kR_{CC}}{L}\right). \nonumber \]
This simple model allows one to estimate spin densities at each carbon center and provides insight into which centers should be most amenable to electrophilic or nucleophilic attack. For example, radical attack at the C\(_5\) carbon of the nine-atom system described earlier would be more facile for the ground state \(\Psi \) than for either \(\Psi\)* or \(\Psi\)'*. In the former, the unpaired spin density resides in \( \psi_5\), which has non-zero amplitude at the \(C_5\) site \(x=\dfrac{L}{2}\); in \(\Psi\)* and \(\Psi\)'*, the unpaired density is in \(\psi_4\) and \(\psi_6\), respectively, both of which have zero density at \(C_5\). These densities reflect the values
\[ \sqrt{\dfrac{2}{L}} \sin \left( \dfrac{n\pi kR_{CC}}{L} \right) \nonumber \]
of the amplitudes for this case in which L = 8 x R\(_{CC}\) for n = 5, 4, and 6, respectively.


